相关试卷

1、在二次函数 $y = a x^{2} + b x - 2$ 中， $x$ 与 $y$ 的几组对应值如表所示。
$x$
…
$- 2$
$0$
$1$
…
$y$
…
$- 2$
$- 2$
$1$
…

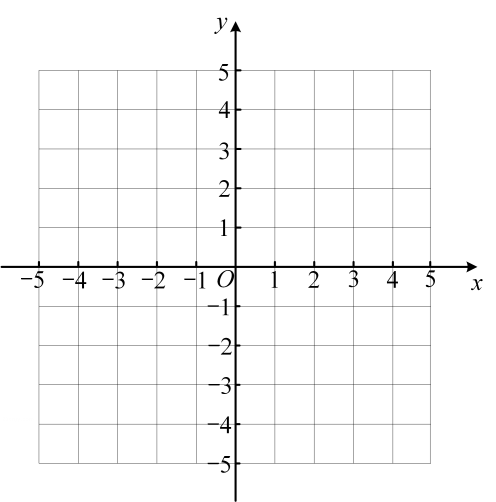(1)、求二次函数的表达式；

(2)、求二次函数图象的顶点坐标，并在给出的平面直角坐标系中画出二次函数的图象；

(3)、将二次函数的图象先向右平移2个单位长度，再向上平移1个单位长度后所得图象与直线 $y = 2$ 相交于 $A$ ， $B$ 两点，请直接写出线段 $A B$ 的长。

查看解析
2、已知关于 $x$ 的一元二次方程 $x^{2} - 3 m x + 2 m^{2} = 0$ 。

(1)、求证：该方程总有两个实数根；

(2)、若 $x_{1}$ ， $x_{2}$ 是此方程的两个实数根，且 $2 x_{1} - x_{2} = 3$ ，求 $m$ 的值。

查看解析
3、如图1，月洞门是中国古典建筑中的一种圆形门洞，形如满月，故称“月洞门”，其形制可追溯至汉代，但真正在美学与功能上成熟于宋代，北宋建筑学家李诫编修的《营造法式》是中国古代最完整的建筑技术典籍之一。
如图2，是古人根据《营造法式》中的“五举法”作出的月洞门的设计图，月洞门呈圆弧形，用 $弧 A C B$ 表示，点 $O$ 是 $弧 A C B$ 所在圆的圆心， $A B$ 是月洞门的横跨， $C D$ 是月洞门的拱高。现在我们也可以用尺规作图的方法作出月洞门的设计图。
如图3，已知月洞门的横跨为 $A B$ ，拱高为 $a$ 。作法如下：
①作线段 $A B$ 的垂直平分线 $M N$ ，垂足为点 $D$ ；
②在射线 $D M$ 上截取 $D C = a$ ；
③连接 $A C$ ，作线段 $A C$ 的垂直平分线交 $C D$ 于点 $O$ ；
④以点 $O$ 为圆心， $O C$ 的长为半径作 $\overset{⏜}{A C B}$ 。
则 $\overset{⏜}{A C B}$ 就是所要作的圆弧。
解答下列问题：

(1)、请你依据以上步骤，用尺规作图的方法在图3中作出月洞门的设计图（保留作图痕迹，不写作法）；

(2)、若 $A B = 1 m$ ， $C D = 2.5 m$ ，求 $⊙ O$ 的半径长。

查看解析
4、某工厂用甲、乙两种原料生产A，B两种产品。每日原料供应量如表一所示，每件产品所需原料及利润如表二所示：
表一
原料
甲
乙
日供应量（kg）
60
80
表二
产品类型
甲原料(kg/件)
乙原料(kg/件)
利润(元/件)
A
2
4
50
B
4
2
60
应市场需求，工厂要求每天生产的B产品数量不少于A产品数量。

(1)、若全部生产B产品，每日最多可生产件；

(2)、工厂每日最大总利润为元。

查看解析
5、如图1，在 $△ A B C$ 中， $∠ A C B = 90 °$ ， $C A = C B$ ，在 $△ C D E$ 中， $∠ D C E = 90 °$ ， $∠ E = 30 °$ ， $A B = C E = 12$ ，点C，B，E在一条直线上。若在图1的基础上，保持 $△ C D E$ 不动，把 $△ A B C$ 绕点C按逆时针方向旋转一定的角度，使得点A落在边DE上(如图2)，则旋转角 $∠ A C D =____°$ 。

查看解析
6、如图，抛物线 $y = a x^{2} + b x + c (a \neq 0)$ 与直线 $y = m x + n (m \neq 0)$ 相交于点 $P (- 2,3)$ ， $Q (5,7)$ ，则关于 $x$ 的方程 $a x^{2} + b x + c = m x + n$ 的解是。

查看解析
7、我国魏晋时期数学家刘徽在为《九章算术》作注时，创立了“割圆术”。如图是研究“割圆术”的一个图形， $弧 A B$ 所在圆的圆心为点 $O$ ，四边形 $A B C D$ 为矩形，边 $C D$ 与 $⊙ O$ 相切于点 $E$ ，连接 $B E$ ， $∠ A B E = 15 °$ ，连接 $O E$ 交 $A B$ 于点 $F$ 。若 $A B = 4$ ，则 $\overset{⏜}{A B}$ 的长为（结果保留 $π$ ）。

查看解析
8、某林业部门考察银杏树苗在一定条件下移植的成活率，所统计的银杏树苗移植成活的相关数据如下表所示：
移植的棵数 $a$
100
300
600
1000
7000
15 000
成活的棵数 $b$
87
279
535
887
6337
13 581
成活的频率 $\frac{b}{a}$ （保留小数点后三位）
0.870
0.930
0.892
0.887
0.905
0.905
根据表中的信息，估计银杏树苗在这个条件下移植成活的概率约为（精确到0.1）。

查看解析
9、写出一个二次函数，使其图象满足：①开口向下；②经过点（0，2）。这个二次函数的解析式可以是。

查看解析
10、如图，在⊙O中，点C是直径AB上的动点(不与点A，B重合)，分别以AC和BC为直径作半圆，记阴影部分Ⅰ的面积为S₁ ，周长为C₁。过点C作 $C D ⊥ A B$ 交⊙O于点D，以CD为直径作圆，记此圆(阴影部分Ⅱ)的面积为S₂ ，周长为C₂。
给出下面四个结论：
①S₁ = S₂； ②S₁ 与S₂ 之和为定值；
③C₁ 为定值；④C₂ 不超过C₁ 的一半。
上述结论中，所有正确结论的序号是（）

A、①② B、③④ C、①②③ D、①③④

查看解析
11、在水分、养料等条件一定的情况下，某植物的生长速度y(厘米/天)和光照强度x(勒克斯)之间存在一定关系。在低光照强度范围( $200 \leq x$ <； 1000)内，y与x近似成一次函数关系；在中高光照强度范围( $x \geq 1000$ )内，y与x近似成二次函数关系。其部分图象如图所示。根据图象，下列结论正确的是（）

A、当 $x \geq 1000$ 时，y随x的增大而减小 B、当x $= 2000$ 时，y有最大值 C、当y $\geq 0$ .6时， $x \geq 3000$ D、当 $y = 0$ .4时， $x = 600$

查看解析
12、已知点A( $- 2$ ， y₁)，B(1，y₂)在抛物线 $y = 2 x$ ² $+ 2 x + 1$ 上，则下列判断正确的是（）

A、1 < y₁ $= y$ ₂ B、y₁ $= y$ ₂ < 1 C、y₁ <1 <y₂ D、y₂ <1 <y₁

查看解析
13、如图， $△ A B C$ 内接于⊙O， $∠ B A C = 30$ °。分别以点A和点B为圆心，大于 $\frac{1}{2} A B$ 的长为半径作弧，两弧交于M，N两点，作直线MN交AC于点D，连接BD并延长交⊙O于点E，连接OA，OE，则 $∠ A O E$ 的度数是（）

A、30° B、50° C、60° D、75°

查看解析
14、一元二次方程 $2 x^{2} - 3 x + 1 = 0$ 的根的情况，下列结论正确的是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法判断根的情况

查看解析
15、如图，将 $∆ A B C$ 绕点A逆时针旋转 $90 °$ 得到 $∆ A D E$ ，若 $A C = 6$ ，连接CE，则CE的长为（）

A、3 B、6 C、 $6 \sqrt{2}$ D、12

查看解析
16、 2025年4月24日，神舟二十号载人飞船成功发射.下列航天图案是中心对称图形的是（）

A、 B、 C、 D、

查看解析
17、在下列事件中，不可能事件是（）

A、投掷一枚硬币，正面向上 B、从只有红球的袋子中摸出黄球 C、通常加热到 $100 ° C$ 时，水沸腾 D、射击运动员射击一次，命中靶心

查看解析
18、如图， $A B C D$ 是正方形， $B C$ 是 $⊙ O$ 的直径，点E是 $⊙ O$ 上的一动点（点E不与点B，C重合），连接 $D E ， B E ， C E$ ．

(1)、若 $∠ E B C = 60 °$ ，求 $∠ E C B$ 的度数；

(2)、若 $D E$ 为 $⊙ O$ 的切线，连接 $D O ， D O$ 交 $C E$ 于点F，求证： $D F = C E$ ；

(3)、若 $A B = 2$ ，过点A作 $D E$ 的垂线交射线 $C E$ 于点M，求 $A M$ 的最小值．

查看解析
19、如图，在Rt△ABC中，∠C=90°，AC=BC，点O是斜边AB的中点，将边长足够大的三角板的直角顶点放在点O处，将三角板绕点O顺时针旋转一个角度α（0°＜α＜90°），记三角板的两直角边与Rt△ABC的两腰AC、BC的交点分别为E、D，四边形CEOD是旋转过程中三角板与△ABC的重叠部分（如图①所示）.那么，在上述旋转过程中：

（1）线段CE与BD具有怎样的数量关系？四边形CEOD的面积是否发生变化？证明你发现的结论；
（2）当三角尺旋转角度为____________时，四边形CEOD是矩形；
（3）若三角尺继续旋转，当旋转角度α（90°＜α＜180°）时，三角尺的两边与等腰Rt△ABC的腰CB和AC的延长线分别交于点D、E（如图②所示）. 那么线段CE与BD的数量关系还成立吗？若成立，给予证明；若不成立，请说明理由。

查看解析
20、解方程： $x (x - 3) = x - 3$ ．

查看解析

上一页 95 96 97 98 99 下一页跳转

产品类型	甲原料(kg/件)	乙原料(kg/件)	利润(元/件)
A	2	4	50
B	4	2	60

移植的棵数 $a$	100	300	600	1000	7000	15 000
成活的棵数 $b$	87	279	535	887	6337	13 581
成活的频率 $\frac{b}{a}$ （保留小数点后三位）	0.870	0.930	0.892	0.887	0.905	0.905

$x$	…	$- 2$	$0$	$1$	…
$y$	…	$- 2$	$- 2$	$1$	…

原料	甲	乙
日供应量（kg）	60	80