相关试卷

1、如果 $x = y$ ，那么根据等式的性质，下列变形正确的是（）

A、 $x + y = 0$ B、 $7 x = 7 y$ C、 $x + 5 = y - 5$ D、 $\frac{x}{4} = \frac{4}{y}$

查看解析
2、在 $1.5 、 - 2 、 - 0.7 、 6 、 15 %$ 中，负有理数有（）

A、2个 B、3个 C、4个 D、5个

查看解析
3、平凉市位于甘肃省东部，是甘肃开放开发的“东大门”，总面积11000平方公里，数据11000用科学记数法表示为（）

A、 $1.1 \times 1 0^{3}$ B、 $11 \times 1 0^{3}$ C、 $1.1 \times 1 0^{4}$ D、 $0.11 \times 1 0^{5}$

查看解析
4、下列各式中，与 $a^{3} b$ 是同类项的为（）

A、 $3 a^{2} b$ B、 $2 a b^{2}$ C、 $- 4 a^{3} b^{3}$ D、 $7 a^{3} b$

查看解析
5、在平面直角坐标系 $x O y$ 中，对于点 $P$ 、点 $M$ 和图形 $G$ ，给出如下定义：在图形 $G$ 上存在点 $Q$ ，使得点 $M$ 是线段 $P Q$ 的中点（ $P$ ， $Q$ 不重合），则称点 $P$ 为图形 $G$ 关于点 $M$ 的“映射点”。
已知正方形 $A B C D$ 的顶点为 $A (- 1,2)$ ， $B (3,2)$ ， $C (3, - 2)$ ， $D (- 1, - 2)$ 。

(1)、已知点 $M$ 的坐标为 $(4,1)$ ，在点 $P_{1} (5,3)$ ， $P_{2} (6, - 1)$ ， $P_{3} (8,4)$ 中，正方形 $A B C D$ 关于点 $M$ 的映射点是.

(2)、已知点 $M (m, - m + 4)$ ，若 $x$ 轴上存在正方形 $A B C D$ 关于点 $M$ 的映射点，直接写出 $m$ 的取值范围；

(3)、已知点 $T (t, 0)$ ，点 $M$ 在半径为 $1$ 的 $⊙ T$ 上，若 $⊙ T$ 上存在正方形 $A B C D$ 关于点 $M$ 的映射点，直接写出 $t$ 的取值范围。

查看解析
6、如图，在 $∆ A B C$ 中， $A B = A C$ ， $∠ B A C = 90 °$ ， $A D$ 为 $∆ A B C$ 的中线， $E$ 是 $A D$ 上一点，连接 $C E$ ，将线段 $C E$ 绕点 $C$ 顺时针旋转 $90 °$ 得到 $C F$ ，过点 $F$ 作 $F G ⊥ D C$ 交 $D C$ 的延长线于点 $G$ 。

(1)、求证： $A D = F G$ ；

(2)、连接 $B F$ ，取 $B F$ 的中点 $H$ ，连接 $A H$ ， $D H$ 。依题意补全图形，用等式表示线段 $A H$ 与 $D H$ 之间的数量关系，并证明。

查看解析
7、在平面直角坐标系 $x O y$ 中，抛物线 $y = x^{2} + b x + 3$ 经过点 $(2,3)$ 。点 $M$ 为抛物线上任意一点，其横坐标为 $m$ ，过点 $M$ 作 $M P ∥ x$ 轴，点 $P$ 的横坐标为 $- 2 m$ 。

(1)、求 $b$ 的值；

(2)、当线段 $M P$ 与抛物线有两个公共点时，求出 $m$ 的取值范围；

(3)、过点 $P$ 作 $P Q ⊥ x$ 轴交抛物线 $y = x^{2} + b x + 3$ 于点 $Q$ ，点 $M$ 在抛物线上运动的过程中，若线段 $P Q$ 的长随 $m$ 的增大而增大，直接写出 $m$ 的取值范围。

查看解析
8、如图，在 $R t ∆ A B C$ 中， $A C = B C$ ， $∠ A C B = 90 °$ ， $D$ 是 $B C$ 上一点， $⊙ O$ 是 $∆ A C D$ 的外接圆。过点 $C$ 作 $⊙ O$ 的切线，交 $A B$ 的延长线于点 $E$ 。

(1)、求证： $∠ E = ∠ D A B$ ；

(2)、若 $B$ 是 $A E$ 的中点，且 $A B = 2 \sqrt{2}$ ，求 $C D$ 的长。

查看解析
9、2025年世界人形机器人运动会在北京举行，其中“篮球投篮人机挑战赛”成为热门项目。篮球飞行的轨迹可近似看作抛物线。以机器人站立点为原点建立平面直角坐标系，篮球飞行的竖直高度 $y$ （单位：米）与水平距离 $x$ （单位：米）满足二次函数关系 $y = a (x - h)^{2} + k (a < 0)$ 。
机器人某次投篮，篮球飞行的水平距离 $x$ 与竖直高度 $y$ 的几组数据如下：
水平距离 $x$ （米）
0
1
2
3
4
5
竖直高度 $y$ （米）
2.0
2.7
3.2
3.5
3.6
3.5

挑战者在同样地点投篮，篮球飞行的竖直高度 $y$ 与水平距离 $x$ 近似满足二次函数关系 $y = - 0.08 (x - 4.32)^{2} + 3.8$ 。

(1)、根据上述数据，直接写出机器人投篮时，篮球飞行的竖直高度的最大值为米，满足的函数关系 $y = a (x - h)^{2} + k (a < 0)$ 是；

(2)、若篮球在水平距离5米处的竖直高度 $y$ 满足 $3.2 \leq y \leq 3.5$ ，视为有效投篮，则机器人投篮（填“有效”或“无效”），挑战者投篮（填“有效”或“无效”）。

查看解析
10、在全球新能源汽车产业蓬勃发展的浪潮中，中国凭借强大的产业实力和技术创新能力脱颖而出，已连续10年保持新能源汽车年产销量全球第一。随着技术迭代加速发展，某新能源汽车的电池成本持续下降，2023年电池成本约为1200元/千瓦时，2025年电池成本约为972元/千瓦时，求这两年该电池成本的年平均下降率。

查看解析
11、某班开展“我爱北京”的综合实践活动，班委会决定设置“山水”“历史”“文学”“艺术”（分别记作A，B，C，D）四个研究主题，并采取小组合作的研究方式。同学们在四张完全相同的不透明卡片的正面分别写上这四个研究主题，卡片背面保持完全相同。

(1)、将这四张卡片背面朝上洗匀后，从中随机抽取一张，抽到的卡片内容是“历史”的概率为；

(2)、各小组从这四张卡片中随机抽取一张，将卡片内容作为本小组的研究主题。将这四张卡片背面朝上洗匀后，小明代表第一小组从中随机抽取一张，记下结果后放回，背面朝上洗匀后，小红代表第二小组从中随机抽取一张。请用列表或画树状图的方法，求这两个小组研究主题不同的概率。

查看解析
12、已知在边长为1个单位长度的小正方形组成的网格中， $△ A B C$ 的三个顶点A，B，C均在格点(小正方形的顶点)上。

(1)、如图1，以边AC的中点O为旋转中心，将 $△ A B C$ 旋转180°，得到 $△ A$ ₁B₁C₁ ，画出 $△ A$ ₁B₁C₁；

(2)、如图2，在图中找一个格点E，使 $∠ A E C + ∠ A B C = 180$ °。

查看解析
13、在二次函数 $y = a x^{2} + b x - 2$ 中， $x$ 与 $y$ 的几组对应值如表所示。
$x$
…
$- 2$
$0$
$1$
…
$y$
…
$- 2$
$- 2$
$1$
…

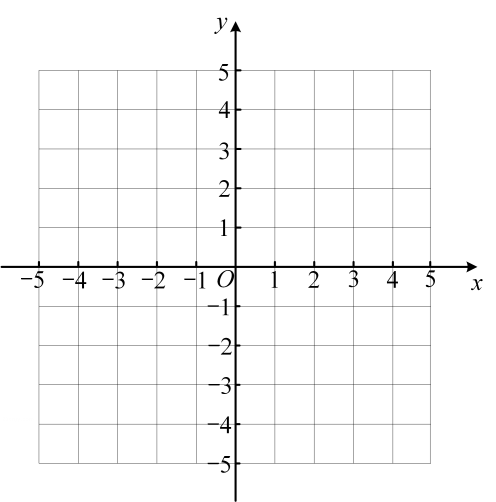(1)、求二次函数的表达式；

(2)、求二次函数图象的顶点坐标，并在给出的平面直角坐标系中画出二次函数的图象；

(3)、将二次函数的图象先向右平移2个单位长度，再向上平移1个单位长度后所得图象与直线 $y = 2$ 相交于 $A$ ， $B$ 两点，请直接写出线段 $A B$ 的长。

查看解析
14、已知关于 $x$ 的一元二次方程 $x^{2} - 3 m x + 2 m^{2} = 0$ 。

(1)、求证：该方程总有两个实数根；

(2)、若 $x_{1}$ ， $x_{2}$ 是此方程的两个实数根，且 $2 x_{1} - x_{2} = 3$ ，求 $m$ 的值。

查看解析
15、如图1，月洞门是中国古典建筑中的一种圆形门洞，形如满月，故称“月洞门”，其形制可追溯至汉代，但真正在美学与功能上成熟于宋代，北宋建筑学家李诫编修的《营造法式》是中国古代最完整的建筑技术典籍之一。
如图2，是古人根据《营造法式》中的“五举法”作出的月洞门的设计图，月洞门呈圆弧形，用 $弧 A C B$ 表示，点 $O$ 是 $弧 A C B$ 所在圆的圆心， $A B$ 是月洞门的横跨， $C D$ 是月洞门的拱高。现在我们也可以用尺规作图的方法作出月洞门的设计图。
如图3，已知月洞门的横跨为 $A B$ ，拱高为 $a$ 。作法如下：
①作线段 $A B$ 的垂直平分线 $M N$ ，垂足为点 $D$ ；
②在射线 $D M$ 上截取 $D C = a$ ；
③连接 $A C$ ，作线段 $A C$ 的垂直平分线交 $C D$ 于点 $O$ ；
④以点 $O$ 为圆心， $O C$ 的长为半径作 $\overset{⏜}{A C B}$ 。
则 $\overset{⏜}{A C B}$ 就是所要作的圆弧。
解答下列问题：

(1)、请你依据以上步骤，用尺规作图的方法在图3中作出月洞门的设计图（保留作图痕迹，不写作法）；

(2)、若 $A B = 1 m$ ， $C D = 2.5 m$ ，求 $⊙ O$ 的半径长。

查看解析
16、某工厂用甲、乙两种原料生产A，B两种产品。每日原料供应量如表一所示，每件产品所需原料及利润如表二所示：
表一
原料
甲
乙
日供应量（kg）
60
80
表二
产品类型
甲原料(kg/件)
乙原料(kg/件)
利润(元/件)
A
2
4
50
B
4
2
60
应市场需求，工厂要求每天生产的B产品数量不少于A产品数量。

(1)、若全部生产B产品，每日最多可生产件；

(2)、工厂每日最大总利润为元。

查看解析
17、如图1，在 $△ A B C$ 中， $∠ A C B = 90 °$ ， $C A = C B$ ，在 $△ C D E$ 中， $∠ D C E = 90 °$ ， $∠ E = 30 °$ ， $A B = C E = 12$ ，点C，B，E在一条直线上。若在图1的基础上，保持 $△ C D E$ 不动，把 $△ A B C$ 绕点C按逆时针方向旋转一定的角度，使得点A落在边DE上(如图2)，则旋转角 $∠ A C D =____°$ 。

查看解析
18、如图，抛物线 $y = a x^{2} + b x + c (a \neq 0)$ 与直线 $y = m x + n (m \neq 0)$ 相交于点 $P (- 2,3)$ ， $Q (5,7)$ ，则关于 $x$ 的方程 $a x^{2} + b x + c = m x + n$ 的解是。

查看解析
19、我国魏晋时期数学家刘徽在为《九章算术》作注时，创立了“割圆术”。如图是研究“割圆术”的一个图形， $弧 A B$ 所在圆的圆心为点 $O$ ，四边形 $A B C D$ 为矩形，边 $C D$ 与 $⊙ O$ 相切于点 $E$ ，连接 $B E$ ， $∠ A B E = 15 °$ ，连接 $O E$ 交 $A B$ 于点 $F$ 。若 $A B = 4$ ，则 $\overset{⏜}{A B}$ 的长为（结果保留 $π$ ）。

查看解析
20、某林业部门考察银杏树苗在一定条件下移植的成活率，所统计的银杏树苗移植成活的相关数据如下表所示：
移植的棵数 $a$
100
300
600
1000
7000
15 000
成活的棵数 $b$
87
279
535
887
6337
13 581
成活的频率 $\frac{b}{a}$ （保留小数点后三位）
0.870
0.930
0.892
0.887
0.905
0.905
根据表中的信息，估计银杏树苗在这个条件下移植成活的概率约为（精确到0.1）。

查看解析

上一页 88 89 90 91 92 下一页跳转

水平距离 $x$ （米）	0	1	2	3	4	5
竖直高度 $y$ （米）	2.0	2.7	3.2	3.5	3.6	3.5

产品类型	甲原料(kg/件)	乙原料(kg/件)	利润(元/件)
A	2	4	50
B	4	2	60

移植的棵数 $a$	100	300	600	1000	7000	15 000
成活的棵数 $b$	87	279	535	887	6337	13 581
成活的频率 $\frac{b}{a}$ （保留小数点后三位）	0.870	0.930	0.892	0.887	0.905	0.905

$x$	…	$- 2$	$0$	$1$	…
$y$	…	$- 2$	$- 2$	$1$	…

原料	甲	乙
日供应量（kg）	60	80