-
1、 已知关于x,y的方程组 , 甲同学看错了字母a解得;乙同学看错了字母b解得 , 则该方程组的解为( )A、 B、 C、 D、
-
2、绿色出行,健康出行,你我同行.某市为了方便市民绿色出行,推出了共享单车服务.图1是某品牌共享单车放在水平地面的实物图,图2是其示意图,其中、都与地面平行,与平行,若 , 则的度数为( )
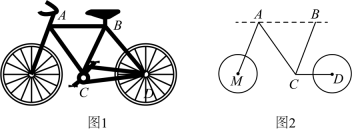 A、 B、 C、 D、
A、 B、 C、 D、 -
3、不改变分式的值,把它的分子与分母中的系数化为整数,下列式子正确的是( )A、 B、 C、 D、
-
4、下列变形是因式分解的是( )A、 B、 C、 D、
-
5、某款风味酸牛奶的营养成分中,碳水化合物含量是蛋白质的4倍,碳水化合物、蛋白质与脂肪的含量共37g.设蛋白质、脂肪的含量分别为(g),(g),可列出方程( )A、 B、 C、 D、
-
6、下列运算正确的是( )A、 B、 C、 D、
-
7、要使分式有意义,的取值应满足( )A、 B、 C、 D、
-
8、如图1,在矩形中, , 点是边上一个动点,点在射线上, . 线段的垂直平分线分别交直线于点、、、 .
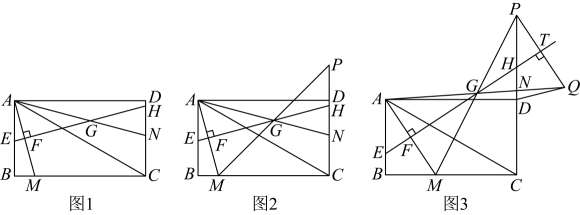 (1)、直接写出°,;(2)、当时,求的值;(3)、如图2,连接并延长交直线于点 .
(1)、直接写出°,;(2)、当时,求的值;(3)、如图2,连接并延长交直线于点 .①求证:;
②如图3,过点作直线的垂线,分别交直线于点 , 连接 , 求线段的最小值.
-
9、定义:在平面直角坐标系中,到两个坐标轴的距离都小于或等于的点叫“阶近轴点”,所有的“阶近轴点”组成的图形记为图形 . 如图所示,所有的“1阶近轴点”组成的图形是以坐标原点为中心,2为边长的正方形区域.
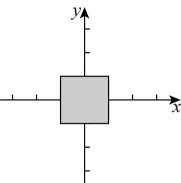 (1)、下列函数图象上存在“1阶近轴点”的是;
(1)、下列函数图象上存在“1阶近轴点”的是;①;②;③ .
(2)、若一次函数的图像上存在“3阶近轴点”,求实数的取值范围;(3)、特别地,当点在图形上,且横坐标是纵坐标的倍时,称点是图形的“阶完美点”,若二次函数的图像上有且只有一个“2阶完美点”,求实数的取值范围. -
10、甲、乙两人从同一地点出发沿同一路线匀速步行前往处参加活动.甲比乙早出发 , 两人途中均未休息,先到达处的人在原地休息等待,直到另一人到达处.两人之间的路程与甲行走的时间的函数图象如图所示.
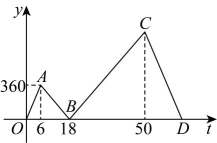 (1)、乙步行的速度为之间的路程为;(2)、当时,求关于的函数表达式;(3)、甲出发多长时间时,两人之间的路程为 .
(1)、乙步行的速度为之间的路程为;(2)、当时,求关于的函数表达式;(3)、甲出发多长时间时,两人之间的路程为 . -
11、如图,点在上,点在外,线段与交于点 , 过点作的切线交直线于点 , 且 .
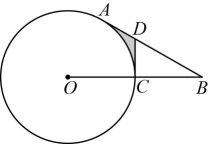 (1)、判断直线与的位置关系,并说明理由;(2)、若 , , 求图中阴影部分的面积.
(1)、判断直线与的位置关系,并说明理由;(2)、若 , , 求图中阴影部分的面积. -
12、实验活动:仅用一把圆规作图.(1)、【任务阅读】如图 , 仅用一把圆规在内部画一点 , 使点在的平分线上.
小明的作法如下:
如图 , 以点为圆心,适当长为半径画弧,分别交射线于点 , 再分别以点、为圆心,大于长为半径画弧,两弧交于点 , 则点为所求点.理由:如图3,连接 , 由作图可知 , ,
又因为 ,
所以 .
所以 ,
所以平分 ,
即点为所求点;
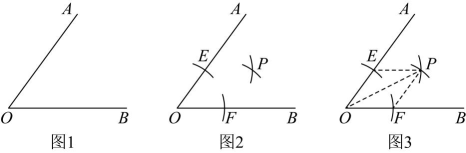 (2)、【实践操作】如图 , 已知直线及其外一点 , 只用一把圆规画一点 , 使点所在直线与直线平行,并给出证明.(保留作图痕迹,不写作法)
(2)、【实践操作】如图 , 已知直线及其外一点 , 只用一把圆规画一点 , 使点所在直线与直线平行,并给出证明.(保留作图痕迹,不写作法)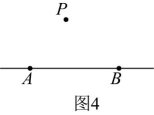
-
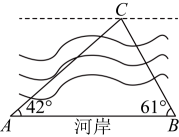
13、小明和小军两位同学对某河流的宽度进行测量,如图所示,两人分别站在同侧河岸上的点、处,选取河对岸的一块石头作为测量点(点在同一水平面内),小明同学在点处测得为 , 小军同学在点处测得为 , 两人之间的距离为60米,求此河流的宽度.(参考数据:)
-
14、某校建议学生利用周末时间积极参加社会实践活动.某一周末有两个项目供学生选择:A文明交通劝导志愿行,B乡村教育关爱行,每名学生只能选择其中一个项目.(1)、甲同学选择A项目的概率为;(2)、请用画树状图的方法,求甲、乙、丙三位同学恰好选择同一项目的概率.
-
15、2025年2月,江苏省教育厅印发《关于在义务教育学校实施“2・15专项行动”的通知》,明确提出“中小学生每天综合体育活动时间不低于2小时”.某校采取多种举措,确保学生每天有充足的体育活动时间,同时监测学生的体质健康情况.为此,学校从全体男生中随机抽取部分学生调查他们的立定跳远成绩,并把成绩分成五档(A档、B档、C档、D档、E档 , 单位:),绘制成统计图.其中部分数据丢失,请结合统计图,完成下列问题:
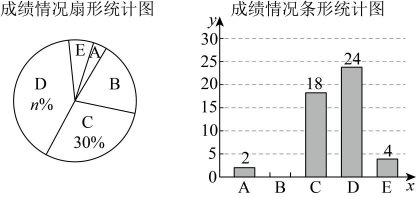 (1)、扇形统计图中的值为 , 条形统计图中“B档”成绩的人数为;(2)、本次抽测中,立定跳远成绩的中位数落在档;(3)、若该校共有1200名男生,请你估计该校立定跳远成绩为“E档”的男生人数.
(1)、扇形统计图中的值为 , 条形统计图中“B档”成绩的人数为;(2)、本次抽测中,立定跳远成绩的中位数落在档;(3)、若该校共有1200名男生,请你估计该校立定跳远成绩为“E档”的男生人数. -
16、先化简,再求值: , 其中 .
-
17、计算: .
-
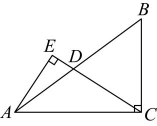
18、如图,在中, , 点在边上(不与A,B重合),过点作 , 垂足为点 , 则的最小值是 .
-
19、方程的两个根分别是 , 则
-
20、一块梯形木板 , 按如图方式设计一个矩形桌面(点在边上).当时,矩形桌面面积最大.
