-
1、已知圆弧所在圆的半径为6,该弧所对的圆心角为90°,则这条弧的长为( )A、2π B、3π C、4π D、6π
-
2、在△ABC中,D、E分别是AB、AC的中点.若DE=4,则BC的长为( )A、2 B、4 C、6 D、8
-
3、一组数据:13,14,14,16,18,这组数据的平均数和众数分别是( )A、15,14 B、14,15 C、14,14 D、15,15
-
4、下列运算正确的是( )A、a2+a4=a6 B、a2•a4=a6 C、(a2)4=a6 D、a4÷a=a4
-
5、2025年春节期间,无锡市65家备案博物馆接待游客总数约819000人次.数据819000用科学记数法表示为( )A、8.19×105 B、81.9×104 C、0.819×105 D、0.819×106
-
6、计算﹣2+3的结果为( )A、﹣5 B、﹣1 C、1 D、5
-
7、 如图1,在正方形ABCD中,点E在AB的延长线上,连结CE,过点A作于点F,分别交正方形的对角线BD和边BC于点G、H.
 (1)、 求证:.(2)、 如图2,连结CG,EG,已知 , 设 , .
(1)、 求证:.(2)、 如图2,连结CG,EG,已知 , 设 , .① 求y关于x的函数表达式.
② 当时,求四边形BECG的面积.
-
8、 已知反比例函数与一次函数的图象均过点 , 且.(1)、 当时,
①求反比例函数和一次函数表达式.
②若点向左平移3个单位长度,再向上平移2个单位长度后,恰好落在的图象上,求n的值.
(2)、 已知点在反比例函数的图象上,都有 , 求m的取值范围. -
9、 甲同学家有一块空地,空地上有一面长为10米的围墙MN,甲打算利用围墙和木栏围一块长方形养鸡场ABCD,已知木栏总长为50米,与墙相对的一面木栏需开一扇宽为2米的门,门不消耗木栏,设AB长为x米.
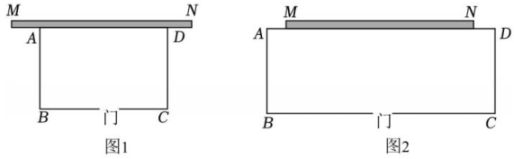 (1)、如图1,当时,
(1)、如图1,当时,① 米(用含x的代数式表示).
② 若围成的养鸡场面积为138平方米,求AB的长.
(2)、如图2,当时,求养鸡场可达到的最大面积. -
10、 对于任意两个非零实数a,b,定义运算“”如下:
, 如: , .
根据上述定义,解决下列问题:
(1)、计算: , .(2)、若 , 求x的值. -
11、 如图,在平行四边形 ABCD 中,. 以点 C 为圆心,CD 为半径作弧,交边 BC 于点 E,连接 AE.
 (1)、 求证:;(2)、 若 , , , 求 ED 的长.
(1)、 求证:;(2)、 若 , , , 求 ED 的长. -
12、 某校为了解八年级男生“引体向上”的水平,随机抽取了50名八年级男生进行调查,并把调查结果绘制成如下未完成的频数表和频数分布直方图(其中每组含前一个边界值,不含后一个边界值),被调查的男生完成“引体向上”的个数均少于25个.
某校八年级50名男生引体向上个数的频数表
组别(个)
频数
0~5
8
5~10
16
10~15
14
15~20
a
20~25
6
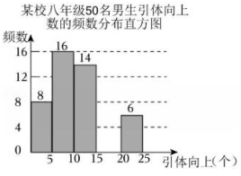 (1)、 求a的值;(2)、 补全频数分布直方图;(3)、 写出这50名八年级男生完成“引体向上”个数的中位数的组别,并说明理由.
(1)、 求a的值;(2)、 补全频数分布直方图;(3)、 写出这50名八年级男生完成“引体向上”个数的中位数的组别,并说明理由. -
13、 解方程:(1)、 ;(2)、 解方程:.
-
14、 计算:(1)、 ;(2)、 计算:;
-
15、 如图,在▱ ABCD中,点E在AB上,点F在CD上,将▱ ABCD沿EF折叠,使得点A与点C重合,得到四边形ECGF,点D的对应点为点G. 若 , , , 则DF的长是.

-
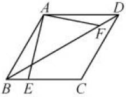
16、 如图,在菱形ABCD中, , , E,F分别是边BC和对角线BD上的动点,且 , 则的最小值为.
-
17、 如图,反比例函数 的图像经过 OABC 的顶点 C,并交 AB 于点 D,已知点 D 是 AB 的中点,连结 OD,CD,若 的面积为 3,则 k 的值为.

-
18、 已知n边形的内角和为 , 则n的值是.
-
19、 在某次歌唱比赛中,小陈“演唱技巧”和“舞台表现”得分分别为9分,8分,若“演唱技巧”和“舞台表现”的权重分别是和 , 则小陈的最终得分为分.
-
20、 如图,在四边形ABCD中,E,F分别是AB,CD的中点,P是对角线AC上一点(点P不与端点重合),过点P作交BC于点Q,交CE于点O. 连结OB,PF,若已知的面积,则一定能求出( )
 A、的面积 B、的面积 C、的面积 D、的面积
A、的面积 B、的面积 C、的面积 D、的面积