-
1、【数学发现】
某校数学兴趣小组进行了如下探究:以△ABC内部任意一点O为中心,画出与△ABC成中心对称的△A'B'C' . 当点O处于不同位置时,从“形”的角度发现两个三角形的重叠部分只可能有两种情况:如图1所示的平行四边形,如图2所示的有三组对边分别平行的六边形(称为“平行六边形”);从“数”的角度发现两个三角形重叠部分的面积在不断变化.
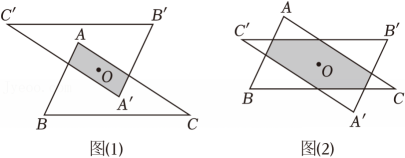
【问题解决】
组员小明选择面积为1的△ABC , 以其内部任意一点O为中心,画出与之成中心对称的△A'B'C' , 探究了下列问题,请你帮他解答.
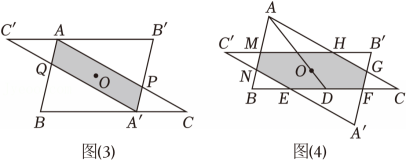
(1)、如图3,BC=2,当点A关于点O的对称点A'落在边BC上时,两个三角形重叠部分为▱AQA'P .①若AA'⊥BC , 求AO的长;(请直接写出答案)
②若▱AQA'P的面积为 , 求A'C的长.
(2)、如图4,点D为BC的中点,点O在AD上,若两个三角形的重叠部分为“平行六边形”EFGHMN , 求“平行六边形”EFGHMN面积的最大值,并指出此时点O的位置. -
2、已知二次函数y=﹣m(m≠0)图象的顶点为A , 与y轴交于点B , 对称轴与x轴交于点C .(1)、若该函数图象经过点 , 求点A的横坐标;(2)、若m<3,点P(2,y1)和Q(4,y2)在该函数图象上,证明:y1>y2;(3)、若△ABC是等腰三角形,求m的值.
-
3、某校数学研究性学习小组为测量物体的高度,开展了如下综合与实践活动.
【活动主题】测量物体的高度
【测量工具】卷尺、标杆
【活动过程】
活动1:测量校内旗杆的高度
该小组在校内进行了旗杆高度的测量活动(示意图1).在点F处竖立标杆EF , 直立在点Q处的小军从点P处看到标杆顶E、旗杆顶M在同一条直线上.已知旗杆底端N与F、Q在同一条直线上,EF=2.8m , PQ=1.4m , QF=2m , FN=16m .
 (1)、求旗杆MN的高度.(2)、活动2:测量南禅寺妙光塔的高度
(1)、求旗杆MN的高度.(2)、活动2:测量南禅寺妙光塔的高度南禅寺妙光塔,简称“妙光塔”,始建于北宋雍熙年间,是无锡著名的文物保护单位之一.该小组为全面了解本土历史文物,决定走出校园去测量妙光塔的高度.他们到达妙光塔后,发现塔顶A和塔底中心B均无法到达.经研究,设计并实施了如下测量活动(示意图2).在地面一条水平步道上的点F处竖立标杆EF , 直立在点Q处的小军从点P处看到标杆顶E、塔顶A在同一条直线上.小军沿FQ的方向走到点Q'处,此时标杆E'F'竖立于F'处,从点P'处看到标杆顶E'、塔顶A在同一条直线上.已知AB、EF、PQ、E'F'和P'Q'在同一平面内,点B、F、Q、F'、Q'在同一条直线上,EF=E'F'=2.8m , PQ=P'Q'=1.4m , FQ=1.2m , F'Q'=2.2m , QQ'=30m .
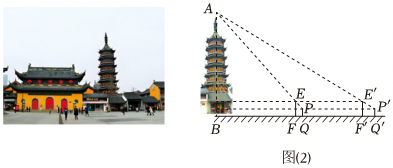
求妙光塔AB的高度.
-
4、如图,AB是⊙O的直径,D是弦AC延长线上的一点,且CD=CA , DB的延长线交⊙O于点E .
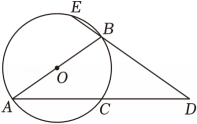 (1)、求证:AB=BD;(2)、若AB=3,cos∠ABE= , 求AD的长.
(1)、求证:AB=BD;(2)、若AB=3,cos∠ABE= , 求AD的长. -
5、如图,AC为正方形ABCD的对角线.
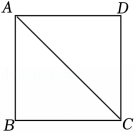 (1)、尺规作图:作AD的垂直平分线l交AD于点E , 在l上确定点F , 使得点F到∠BAC的两边距离相等;(不写作法,保留痕迹)(2)、在(1)的条件下,求∠EFA的度数.(请直接写出∠EFA的度数)
(1)、尺规作图:作AD的垂直平分线l交AD于点E , 在l上确定点F , 使得点F到∠BAC的两边距离相等;(不写作法,保留痕迹)(2)、在(1)的条件下,求∠EFA的度数.(请直接写出∠EFA的度数) -
6、2025年1月14日,教育部办公厅印发了《中小学科学教育工作指南》(以下简称《指南》),旨在推动中小学科学教育更加重视激发学生好奇心、想象力、探求欲,培育具备科学家潜质、愿意献身科学研究事业的青少年群体.某校为落实《指南》要求,准备在七年级开设“3D打印”“航模”“机器人”“无人机”共四类科技社团(每名学生必选且仅选一个社团).为了解学生参加各社团的意向,现随机抽取七年级部分学生进行问卷调查,并对问卷数据进行收集、整理、描述和分析,部分信息如下:
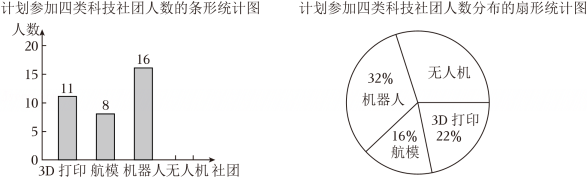
请根据以上信息,解答下列问题:
(1)、本次调查的样本容量为 ▲ ,并将条形统计图补充完整;(画图后请标注相应的数据)(2)、若该校七年级共有1000名学生,请估计计划参加“机器人”社团的学生人数;(3)、根据上述统计分析情况,请你为该校科技社团活动的顺利开展给出一条合理建议. -
7、一只不透明的袋子中装有标号分别为1,2,3,4的4个球,这些球除标号外都相同.(1)、将球搅匀,从中任意摸出1个球,摸到标号为2的球的概率是 ;(2)、将球搅匀,从中任意摸出1个球,记录标号后不放回,再从袋子中任意摸出1个球,记录标号.求两次摸到的球标号均小于3的概率.(请用“画树状图”或“列表”等方法写出分析过程)
-
8、如图,在矩形ABCD中,点E在CB延长线上,点F在BC延长线上,且BE=CF , 连接AE、DF .

求证:
(1)、△ABE≌△DCF;(2)、∠EAD=∠FDA . -
9、先化简,再求值: , 其中m=3.
-
10、(1)、解方程:x2﹣2x﹣2=0;(2)、解不等式组: .
-
11、在平行四边形纸片ABCD中,∠ABC=60°,AB=4,BC=8.现将该纸片折叠,折痕与纸片ABCD的两边交于点E、F . 若E与A重合,F在BC上,且EF⊥BC , 则被折痕分成的△EBF与四边形EFCD的面积的比为 ;若折痕EF将纸片ABCD分成两个四边形,且被分成的两个四边形的面积的比为1:3,则折痕EF长的取值范围是 .
-
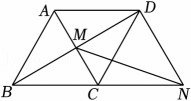
12、如图,菱形ABCD的边长为2,∠ABC=60°,对角线AC、BD相交于点M . 过点D作AC的平行线交BC的延长线于点N , 连接MN . 则MN的长为 .
-
13、如图,AB与⊙O相切于点B , 连接BO , 过点O作BO的垂线OC , 交⊙O于点C , 连接AC , 交线段OB于点D . 若AB=3,OC=2,则tanA的值为 .

-
14、正七边形的内角和为 度.
-
15、请写出命题“若a>b , 则a+1>b+1”的逆命题: .
-
16、请写出单项式a2b的一个同类项: .
-
17、若函数y1的图象上存在点P , 函数y2的图象上存在点Q , 且P、Q关于y轴对称,则称函数y1和y2具有“对偶关系”,此时点P或点Q的纵坐标称为“对偶值”.下列结论:
①函数y1=2x+3与函数y2=﹣x+1不具有“对偶关系”;
②函数y1=2x+3与函数y2=﹣x+1的“对偶值”为﹣1;
③若1是函数y1=kx+3与函数y2=的“对偶值”,则k=2;
④若函数y1=﹣2x+b(﹣2≤x≤﹣1)与函数y2=(x>0)具有“对偶关系”,则3≤b≤ .
其中正确的是( )
A、①④ B、②③ C、①③④ D、②③④ -
18、如图,在平面直角坐标系中,O为坐标原点,Rt△OBA的直角边OB在x轴上,AO、AB分别与反比例函数y=(k>0,x>0)的图象相交于点C、D , 且C为AO的中点,过点C作x轴的垂线,垂足为E , 连接DE . 若△BDE的面积为 , 则k的值为( )
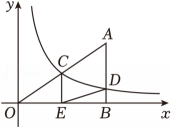 A、 B、 C、5 D、10
A、 B、 C、5 D、10 -
19、小亮与小红周末去十里明珠堤的环湖绿道上骑行,小亮的速度是小红速度的1.2倍,两人各自骑行了6km , 小亮骑行时间比小红少用了4min . 设小红的骑行速度为x km/h , 则可列方程为( )A、 B、 C、 D、
-
20、分解因式a3﹣4a的结果是( )A、a(a2+4) B、a(a﹣4) C、a(a+2)(a﹣2) D、a(a2﹣1)