-
1、已知二次函数 (a 为常数且 ).(1)、 当函数图象经过 (4,0),求该二次函数的表达式.(2)、 若 , 判断该二次函数图象与 x 轴的交点个数并证明.(3)、 若该函数图象上有两点 , 其中 , 若 , .
求证:.
-
2、为了增加趣味性,万岁山旅游城把传统的抛绣球项目进行改良,他们定制了一种器械,类似中国古代一种投石器,为了解发射平台高度对绣球飞行轨迹的影响,我们可以设定不同的发射平台高度,并分别记录绣球在不同水平距离上的飞行高度. 分析不同发射平台高度下绣球的飞行轨迹. 通过比较不同高度下绣球的飞行高度和飞行距离,我们可以得出发射平台高度对绣球运动轨迹的具体影响. 从而有目的地调整发射高度,通过实验发现绣球运动轨迹是抛物线的一部分,并且在离发射点水平距离18米处达到距地面最大高度18米;在离发射点水平距离6米处,距地面高度10米.
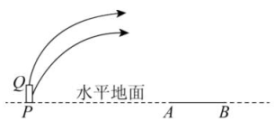
问题解决:
(1)、任务1:确定函数表达式. 设绣球离发射点水平距离为x,距地面高度为y. 求出y关于x的函数表达式;(2)、任务2:探究飞行距离,当绣球从地面发出到落地(高度为0m)时,飞行的水平距离是多少;(3)、任务3:如图,工作人员在水平地面上设置一个高度可以变化的发射平台PQ,当弹射口高度变化时,绣球被弹出后的飞行轨迹形状不变,可视为抛物线上下平移得到,点P、A、B在一条直线上,已知 , , 游客小李站在线段AB(包括点A、B)上,为了确保他能抢到绣球,求发射台PQ的变化范围. -
3、如图,抛物线 与 x 轴交于 A, B 两点,与 y 轴交于点 C,已知 , .
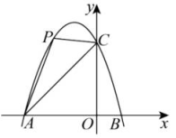 (1)、 求抛物线的解析式;(2)、 第二象限内的点 P 在该抛物线上,求 面积的最大值.
(1)、 求抛物线的解析式;(2)、 第二象限内的点 P 在该抛物线上,求 面积的最大值. -
4、某学校计划建一个长方形种植园,如图,种植园的一边靠墙,其余边用总长为24m的篱笆围成,已知墙a长为10m,设这个种植园垂直于墙的一边长为x(m),种植园面积为.
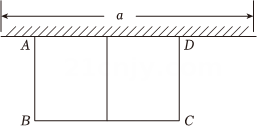 (1)、求y与x的函数关系式,并写出自变量x的取值范围;(2)、根据实际需要,要求这个种植园的面积为 , 求篱笆AB的长.
(1)、求y与x的函数关系式,并写出自变量x的取值范围;(2)、根据实际需要,要求这个种植园的面积为 , 求篱笆AB的长. -
5、如图,抛物线 和直线 交于 A,B 两点.
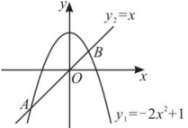 (1)、 求 A,B 两点的坐标;(2)、 根据图象,写出当 x 取何值时, .
(1)、 求 A,B 两点的坐标;(2)、 根据图象,写出当 x 取何值时, . -
6、已知二次函数的顶点坐标为(2,-1),且图像经过点(-3,24).(1)、求函数解析式;(2)、求函数图象与坐标轴交点坐标.
-
7、已知二次函数 , 当 时, , 时,.(1)、 求 a,c 的值;(2)、 当 时,求函数 y 的值.
-
8、已知 是关于 x 的二次函数. 求 m 的值及函数表达式.
-
9、 二次函数 , 当 时,对于每一个 x 的值, 始终成立,则 a 的取值范围是.
-
10、 如图,在相距 2m 的两棵树上拴了一根绳子做成一个简易秋千,拴绳子的地方都高出地面 2.6m,绳子自然下垂近似呈抛物线形,当身高 1.1m 的小妹距较近的那棵树 0.5m 时,头部刚好接触到绳子,则绳子的最低点距地面的距离为m.

-
11、 已知抛物线 经过点 (1,1),则代数式 的值为.
-
12、 若抛物线 经过 和 两点,则 .
-
13、 已知点 , 在抛物线(k 为常数)上,则 , 的大小关系是.
-
14、 请写出一个开口向上,对称轴为y轴的抛物线的表达式:.
-
15、 已知函数的图象如图所示,若直线与该图象有公共点,则k的最大值与最小值的和为( )
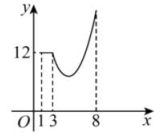 A、2 B、12 C、15 D、17
A、2 B、12 C、15 D、17 -
16、 已知二次函数的图象如图所示,有下列4个结论,其中正确的结论是( )
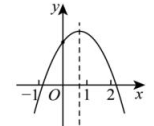 A、 B、 C、 D、
A、 B、 C、 D、 -
17、 如图所示,二次函数与反比例函数的图象大致是( )A、
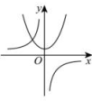 B、
B、 C、
C、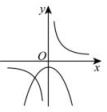 D、
D、
-
18、 某湖面上有一座抛物线形拱桥,按如图所示的方式建立平面直角坐标系,得到抛物线的函数解析式为 , 正常水位时,水面宽 AB 为 16m,此时拱顶 O 到水面 AB 的距离为( )
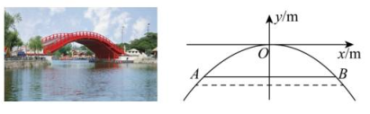 A、4m B、3m C、2m D、1m
A、4m B、3m C、2m D、1m -
19、 已知二次函数的图象如下图所示,关于该函数在所给自变量取值范围内,下列说法中正确的是( )
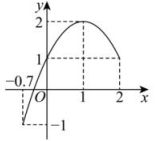 A、有最小值0,有最大值2 B、有最小值-1,有最大值0 C、有最小值-1,有最大值2 D、有最小值-1,无最大值
A、有最小值0,有最大值2 B、有最小值-1,有最大值0 C、有最小值-1,有最大值2 D、有最小值-1,无最大值 -
20、 将二次函数 的图象向右平移 1 个单位,再向下平移 2 个单位后,所得抛物线为( )A、 B、 C、 D、