-
1、如图，P是∠AOB的平分线OC上的一点，过点P分别作OA，OB的垂线，垂足分别为点D，H，E是线段OD上一点，F是线段OH上一点，EF与OC交于点G，且DE=FH.
求证：OP是线段EF的垂直平分线.
-
2、如图所示，在长方形硬纸片的右下角画有一个圆，小丽想把这张硬纸片剪成两块，使两块硬纸片的面积相等，并且圆被分在两块硬纸片中的面积也相等.你认为小丽的想法能实现吗?若能，请你画图说明剪的方法.
-
3、如图所示，O是四边形ABCD中的一点，AB=CD，∠AOB=∠COD，∠BAD=∠CDA，作OE⊥AD，垂足为E，若AE=DE.
求证：线段BC的垂直平分线一定经过点O.
-
4、如图所示，在7×6的正方形网格中，选取14个格点，以其中三个格点为顶点画出△ABC，请你以选取的格点为顶点再画出一个三角形，且分别满足下列条件：
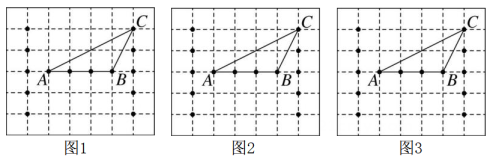(1)、图1中所画的三角形与△ABC组成的图形是轴对称图形.(2)、图2中所画的三角形与△ABC组成的图形是中心对称图形.(3)、图3中所画的三角形与△ABC的面积相等，但不全等. -
5、如图，已知锐角三角形ABC，∠B=48°，请用尺规作图法，在△ABC内部求作一点P.使PB=PC，且∠PBC=24°.(保留作图痕迹，不写作法)
-
6、如图，BD垂直平分线段AC，AE⊥BC，垂足为E，交BD于点P，PE=3 cm，则P点到直线AB的距离是cm.
-
7、如图，AB⊥BC，AB=BC=2 cm，弧OA与弧OC关于点O中心对称，则线段AB，BC，弧OC，弧OA所围成的图形面积是 cm2.
-
8、如图，△AOC和△AOB关于直线AO对称，△DOB和△AOB关于直线BO对称，OC与BD交于点E.若∠C=15°，∠D=25°，则∠BEC的度数为.
-
9、如图，在△ABC中，AB=AC，AD，CE是△ABC的两条中线，P是AD上一个动点，则下列线段的长度等于PB+PE的最小值的是( )
A、BC B、CE C、AD D、AC -
10、如图，在△ABC中，AB=AC，AD是∠BAC的平分线，DE⊥AB，DF⊥AC，垂足分别是E，F，则下列四个结论：①AD上任意一点到点C、点B的距离相等；②AD上任意一点到AB，AC的距离相等；③BD=CD，AD⊥BC；④∠BDE=∠CDF.其中，正确的个数是( )
A、1 B、2 C、3 D、4 -
11、数轴上点A，B的位置如图所示，若点B关于点A的对称点为C，则点C表示的数为( )
A、3 B、-5 C、5 D、-3 -
12、如图，AD是∠BAC的平分线，DE⊥AB于点E，S△ABC=9，DE=2，AC=4，则AB的长是( )
A、3 B、4 C、6 D、5 -
13、如图所示的长方形纸片，先沿虚线按箭头方向向右对折，接着将对折后的纸片沿虚线剪下一个小圆和一个小三角形，然后将纸片打开是下列图中的哪一个( )
A、
B、
C、
D、
-
14、如图所示，图中的两个三角形关于直线l成轴对称，根据图中标注的数据，得∠x的度数为( )
A、25° B、35° C、40° D、70° -
15、如图，是小亮在某时刻从镜子里看到镜子对面电子钟的像，则这个时刻是 ( )
A、10：21 B、10：51 C、21：10 D、15：01 -
16、下列说法中，正确的是( )A、两个全等的三角形一定关于某条直线对称 B、两个图形关于某条直线对称，对应点一定在直线两旁 C、成轴对称的两个图形的对应点连线的垂线，就是它们的对称轴 D、关于某条直线对称的两个三角形是全等三角形
-
17、如图是一个由六个正方形组成的网格.现在嘉嘉想再涂上一个正方形，使四个阴影正方形所组成的图形是中心对称图形，则嘉嘉应该涂( )
A、①或② B、② C、②或③ D、③ -
18、如图所示的图案是由六个全等的菱形(各边相等的四边形)拼成的，它也可以看作是以一个图案为“基本图案”，通过旋转得到的.以下图案中，不能作为“基本图案”的是( )
A、
B、
C、
D、
-
19、下列图案中，既是轴对称图形又是中心对称图形的是( )A、
B、
C、
D、
-
20、在中， ， .点在的平分线所在的直线上.
(1)、如图①，当点在的外部时，过点作于 ， 作交的延长线于 ， 且.求证：点在线段的垂直平分线上；(2)、如图②，当点在线段上时，若 ，平分 ， 交于点 ， 交于点 ， 过点作 ， 交于点.①求的大小；
②若 ， ， 求的长度.
(3)、如图③，过点的直线 ， 若 ， ， 点到三边所在直线的距离相等，则点到直线的距离是.