相关试卷

1、为开展好校园足球活动，某些学校计划联合购买一批足球运动装备，经市场调查，甲、乙两商场分别以同样的价格出售同种品牌的足球队服和足球．已知每套队服比每个足球贵 $20$ 元，购买一套队服和一个足球共需花费 $180$ 元．

(1)、求每套队服和每个足球的售价分别是多少？

(2)、甲商场推出的优惠方案是：每购买 $10$ 套队服，送一个足球；乙商场推出的优惠方案是：若购买队服超过 $90$ 套，则队服原价，但购买足球打八折．若计划一共购买 $100$ 套队服和 $m (m > 10)$ 个足球．
①请用含 $m$ 的代数式分别表示出到甲商场和乙商场购买装备所花的费用；
②若学校的预算是 $12000$ 元，选择在哪家商场购买的足球更多？

查看解析
2、O为原点，点A、B、C在数轴上的位置如图所示， $A O = B C = 5, O B = 10$ ，在C点处有一挡板．D、E为数轴上两动点，动点D从A点出发，以3个单位/秒的速度沿 $B A$ 方向运动；同时，动点E从B点出发，以2个单位/秒的速度沿 $B C$ 方向运动，碰到挡板后以原速的2倍反向运动，设运动的时间为t秒．

(1)、A点对应的数为；B点对应的数为；C点对应的数为；

(2)、若 $D E = 19$ ，求t的值；

(3)、M为 $C E$ 的中点，N为 $B D$ 中点，当 $t < \frac{5}{2}$ 时，若 $4 M C + k \cdot M N$ 的值与t无关，求k的值．

查看解析
3、一天，某客运公司的甲、乙两辆客车分别从相距380千米的A、B两地同时出发相向而行，并以各自的速度匀速行驶，两车行驶2小时时甲车先到达服务区C地，此时两车相距20千米，甲车在服务区C地休息了20分钟，然后按原速度开往B地；乙车行驶2小时10分钟时也经过C地，未停留继续开往A地．

(1)、乙车的速度是千米/小时，B、C两地的距离是千米；A、C两地的距离是千米

(2)、求甲车的速度；

(3)、这一天，乙车出发多长时间，两车相距200千米？

查看解析
4、解方程

(1)、 $4 x - 3 (20 - x) = - 4$

(2)、 $\frac{3 x - 1}{4} = \frac{5 x - 7}{6} + 1$ ．

查看解析
5、若 $(m - 3) x^{| m | - 2} = 5$ 是关于 $x$ 的一元一次方程，则 $m =$ ．

查看解析
6、若关于 $x$ 的一元一次方程 $\frac{1}{2024} x + a = 2 x + b$ 的解为 $x = - 3$ ，那么关于 $y$ 的一元一次方程 $\frac{1}{2024} (y + 1) + a = 2 y + 2 + b$ 的解为．

查看解析
7、如图，各图形都是由面积为1的小正方形按一定的规律组成的，其中，第1个图形中的小正方形有9个，第2个图形中的小正方形有14个，……，按此规律，若第 $n$ 个图形中的小正方形有2024个，则 $n$ 的值为．

查看解析
8、若关于x的多项式 $2 x^{3} + (a + 3) x^{2} + x - 1 - b x$ 不含二次项和一次项，则 $a + b$ 的值为．

查看解析
9、在数轴上点A表示的数为a，点B表示的数为b，且a，b满足 $| a - 20 | + (b + 6)^{2} = 0$ ．点O是数轴原点．如图，将一根长度为6个单位的木棒放在数轴上，木棒的右端与数轴上的B点重合，以每秒2个单位长度的速度向点A移动，木棒出发6秒后，动点P从B点出发，以每秒3个单位长度的速度向点A移动，且当点P到达A点时，木棒与点P同时停止移动，设点P移动的时间为t秒，当t为（）时，P点恰好距离木棒2个单位长度．

A、3秒 B、4秒 C、14秒 D、4秒或14秒

查看解析
10、已知关于x的一元一次方程 $\frac{x}{2019} + 5 = 2019 x + m$ 的解为 $x = 2018$ ，那么关于y的一元一次方程 $\frac{5 - y}{2019} + 5 = 2019 (5 - y) + m$ 的解为（）

A、2023 B、-2013 C、2013 D、-2023

查看解析
11、下列结论：
①若 $x = 1$ 是关于x的方程 $a + b x + c = 0$ 的一个解，则 $a + b + c = 0$ ；
②若 $b = 2 a$ ，则关于x的方程 $a x + b = 0 (a \neq 0)$ 的解为 $x = - \frac{1}{2}$ ；
③若 $- a + b + c = 1$ ，且 $a \neq 0$ ，则 $x = - 1$ 一定是方程 $a x + b + c = 1$ 的解．
其中正确的结论有（）

A、3个 B、2个 C、1个 D、0个

查看解析
12、某商店将一种书包按进价提高 $30 %$ 作为标价，然后再按标价9折出售，这样卖出一个书包可盈利8.5元．这种书包每个进价为（）元．

A、50 B、58.5 C、42.5 D、60

查看解析
13、若方程 $\frac{2 x}{3} = 1 - \frac{- x + 1}{2}$ 和 $2 x - m = 3 m + 1$ 的解相同，则m的值为（）

A、 $2$ B、 $3$ C、 $\frac{5}{4}$ D、 $1$

查看解析
14、解方程 $\frac{1 - 2 x}{3} = \frac{3 x}{2} - 1$ ，下列去分母的过程正确的是（）

A、 $2 (1 - 2 x) = 9 x - 1$ B、 $2 (1 - 2 x) = 3 x - 6$ C、 $1 - 2 x = 9 x - 6$ D、 $2 (1 - 2 x) = 9 x - 6$

查看解析
15、明代读本《原本直指算法统宗》中有这样一个问题：隔墙听得客分银，不知人数不知银，七两分之多四两，九两分之少半斤，其大意：有一群人分银子，若每人分七两，则剩余四两；若每人分九两，则还差八两，问人、银子各多少？设该问题中有x人，则可列方程（）

A、 $7 x + 4 = 9 x - 8$ B、 $7 x - 4 = 9 x + 8$ C、 $\frac{x + 4}{7} = \frac{x - 8}{9}$ D、 $\frac{x - 4}{7} = \frac{x + 8}{9}$

查看解析
16、已知 $x = 3$ 是关于x的方程： $4 + a x = 3$ 的解，那么a的值是（）

A、 $\frac{1}{3}$ B、 $- \frac{1}{3}$ C、 $- 2$ D、 $- \frac{1}{2}$

查看解析
17、已知 $a = b$ ，下列结论不一定正确的是（）

A、 $a + 2 = b + 2$ B、 $a - 3 = b - 3$ C、 $5 a = 5 b$ D、 $\frac{a}{c} = \frac{b}{c}$

查看解析
18、小强和小伟都喜欢放风筝．一天放学后他们互相配合又放起了风筝（如图所示），小伟想测量风筝的铅直高度 $C E$ ，于是他进行了如下测量：①测得小强牵线的手到风筝的水平距离 $B D$ 为 $15 m$ ；②根据小强手中剩余线的长度计算出风筝线 $B C$ （假设 $B C$ 是直的线）的长为 $39 m$ ；③小强牵线的手离地面的距离 $D E$ 为 $1.5 m$ ．

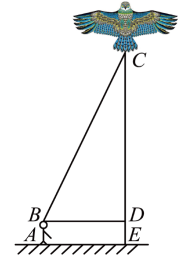(1)、求此时风筝的铅直高度 $C E$ ．

(2)、若小强想使风筝沿 $C D$ 方向下降 $16 m$ （不考虑其他因素），则他应该收线多少米？

查看解析
19、如图，河岸上 $A$ 、 $B$ 两点相距 $25 k m$ ， $C$ 、 $D$ 为两村庄， $D A ⊥ A B$ ， $C B ⊥ A B$ ，垂足分别为 $A$ 、 $B$ ，已知 $A D = 15 k m$ ， $B C = 10 k m$ ，现要在河岸 $A B$ 上建一水厂 $E$ 向 $C$ ， $D$ 两村输送自来水，当水厂E建在距A点多少千米处时，水厂到两村的距离相等？并证明你的结论．

查看解析
20、如图，在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $△ A C D$ 沿 $A D$ 折叠，使得点C落在斜边 $A B$ 上的点E处．

(1)、求证： $△ B D E ∽ △ B A C$ ；

(2)、已知 $A C = 6 ， B C = 8$ ，求线段 $D E$ 的长度．

查看解析

上一页 582 583 584 585 586 下一页跳转