相关试卷

1、如图所示，AD平分∠BAC，交BC于点D，DE⊥AB于点E，DF⊥AC于点F.若S_△ABC=12，DF=2，AC=3，则AB的长是( ）

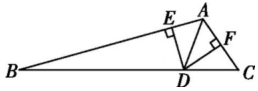A、2 B、4 C、7 D、9

查看解析
2、四边形ABCD的边长如图所示，∠BAD=90°，∠ABC=120°，E为边AD上一动点(不与A，D两点重合)，连接BE，将△ABE沿直线BE折叠，点A的对应点为点F，则点C与点F之间的距离不可能是( )

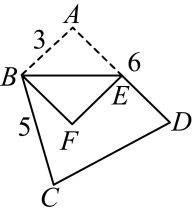
A、3 B、4 C、5 D、8

查看解析
3、将一张正方形纸片按如图所示的步骤，通过折叠得到图④，在CA，CB上各取一点连成虚线，沿该虚线剪去一个角，剩余部分展开铺平后得到的图形可能是( )

A、 B、 C、 D、

查看解析
4、下列说法正确的是( )

A、等腰三角形的对称轴是底边的中线 B、等腰三角形顶角的平分线是它的一条对称轴 C、等腰三角形任意两个角相等 D、三角形的三条高所在的直线一定交于一点

查看解析
5、下列四种图案中，可以看作轴对称图形的是( )

A、 B、 C、 D、

查看解析
6、如图①所示，每个小正方形的边长为1.
① ②

(1)、图中阴影部分的面积是 ▲ ，边长是 ▲ ，并在数轴上(图②)准确地作出表示阴影正方形边长的点.

(2)、已知x为阴影正方形边长的小数部分，y为 $\sqrt{15}$ 的整数部分.
求：①x，y的值；
②(x+y)²的算术平方根.

查看解析
7、

(1)、借助计算器计算下列各题：
① $\sqrt{1^{3}}$ =；
② $\sqrt{1^{3} + 2^{3}}$ =；
③ $\sqrt{1^{3} + 2^{3} + 3^{3}}$ =；
④ $\sqrt{1^{3} + 2^{3} + 3^{3} + 4^{3}}$ =.

(2)、从上面的计算结果中，你发现了什么规律?请用数学式子写出来.

(3)、利用你发现的规律计算： $\sqrt{1^{3} + 2^{3} + … + 100^{3}}$ =.

查看解析
8、(10分)定义：已知a，b都是实数，若a+b=3，则称a与b是关于3的“实验数”.

(1)、4与是关于3的“实验数”.

(2)、 $\sqrt{2}$ 与y是关于3的“实验数”，求y的值，并说出表示y的值的点在如图所示的数轴上的位置(写序号).

(3)、若m= $\sqrt{2}$ -6，判断m与9- $\sqrt{2}$ 是否为关于3的“实验数”，并说明
理由.

查看解析
9、现有一张长方形绣布，长、宽之比为4∶3，绣布面积为588 cm².

(1)、求绣布的周长.

(2)、刺绣师傅想利用这张绣布裁出一张面积为375 cm²的完整圆形绣布来绣花鸟图，她能够裁出来吗?请说明理由.(π取3)

查看解析
10、把下列各数填入相应的集合内：
- $\frac{2}{7}$ ， $\sqrt[3]{36}$ ， -π+2 010， $\sqrt{9}$ ， 3.141 592 6，-|- $\sqrt{100}$ |，0， $\sqrt{2}$ -1， $\frac{\sqrt{3}}{2}$ ， - $\sqrt{8}$ .
整数集合：{                …}；
分数集合：{                 …}；
无理数集合：{               …}.

查看解析
11、如图所示，实数- $\sqrt{5}$ ， $\sqrt{15}$ ， m在数轴上所对应的点分别为A，B，C，点B关于原点的对称点为D.若m为整数，则m的值为.

查看解析
12、已知m是 $\sqrt[3]{13}$ 的整数部分，n是 $\sqrt{13}$ 的小数部分，则m-n的值为.

查看解析
13、发生交通事故后，交通警察通常根据刹车后车轮滑过的距离估计车辆行驶的速度，所用的经验公式是v=16 $\sqrt{d f}$ ，其中v表示车速(单位：km/h)，d表示刹车后车轮滑过的距离(单位：m)，f表示摩擦因数.在某次交通事故调查中，测得d=20 m，f=1.2，则肇事汽车的车速大约是.( $\sqrt{24}$ ≈4.90，结果精确到1 km/h)

查看解析
14、有一个数值转换机，原理如图所示.当输入的x=81时，输出的y=
.

查看解析
15、比较大小：32 $\sqrt{2}$ ； $\frac{\sqrt{5} - 1}{2}$ $\frac{5}{8}$ .(填“>”或“<”)

查看解析
16、计算： $\sqrt[3]{- 125}$ + $\sqrt{4}$ =.

查看解析
17、 $\sqrt{81}$ 的平方根是， 9²的平方根是， -5是的立方根.

查看解析
18、如图所示，长方形ABCD的边AD长为2，AB长为1，点A在数轴上表示的数是-1，以点A为圆心，对角线AC长为半径画弧，交数轴于点E，点E表示的实数是( )

A、 $\sqrt{5}$ +1 B、 $\sqrt{5}$ -1 C、 $\sqrt{5}$ D、1- $\sqrt{5}$

查看解析
19、根据表中的信息判断，下列结论正确的有( )
x
11
11.1
11.2
11.3
11.4
11.5
11.6
11.7
11.8
11.9
12
x²
121
123.21
125.44
127.69
129.96
132.25
134.56
136.89
139.24
141.61
144
①128的算术平方根比11.4大；② $\sqrt{13.924}$ =1.18；③只有2个正整数n满足11.6< $\sqrt{n}$ <11.7；④根据表中数据的变化趋势，可以推断出12.1²比144大2.39.

A、1个 B、2个 C、3个 D、4个

查看解析
20、如图所示，在数轴上表示实数 $\sqrt{13}$ -3的点可能是( )

A、点A B、点B C、点C D、点D

查看解析

上一页 576 577 578 579 580 下一页跳转

x	11	11.1	11.2	11.3	11.4	11.5	11.6	11.7	11.8	11.9	12
x²	121	123.21	125.44	127.69	129.96	132.25	134.56	136.89	139.24	141.61	144