版本：

全部人教A版（2019）人教B版（2019）北师大版（2019）苏教版（2019）上教版（2020）人教新课标A版人教新课标B版苏教版北师大版湘教版沪教版人教版（旧版）

相关试卷

1、如图，在正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中，点 $P$ 在线段 $B_{1} C$ 上运动，则下列结论正确的是（）

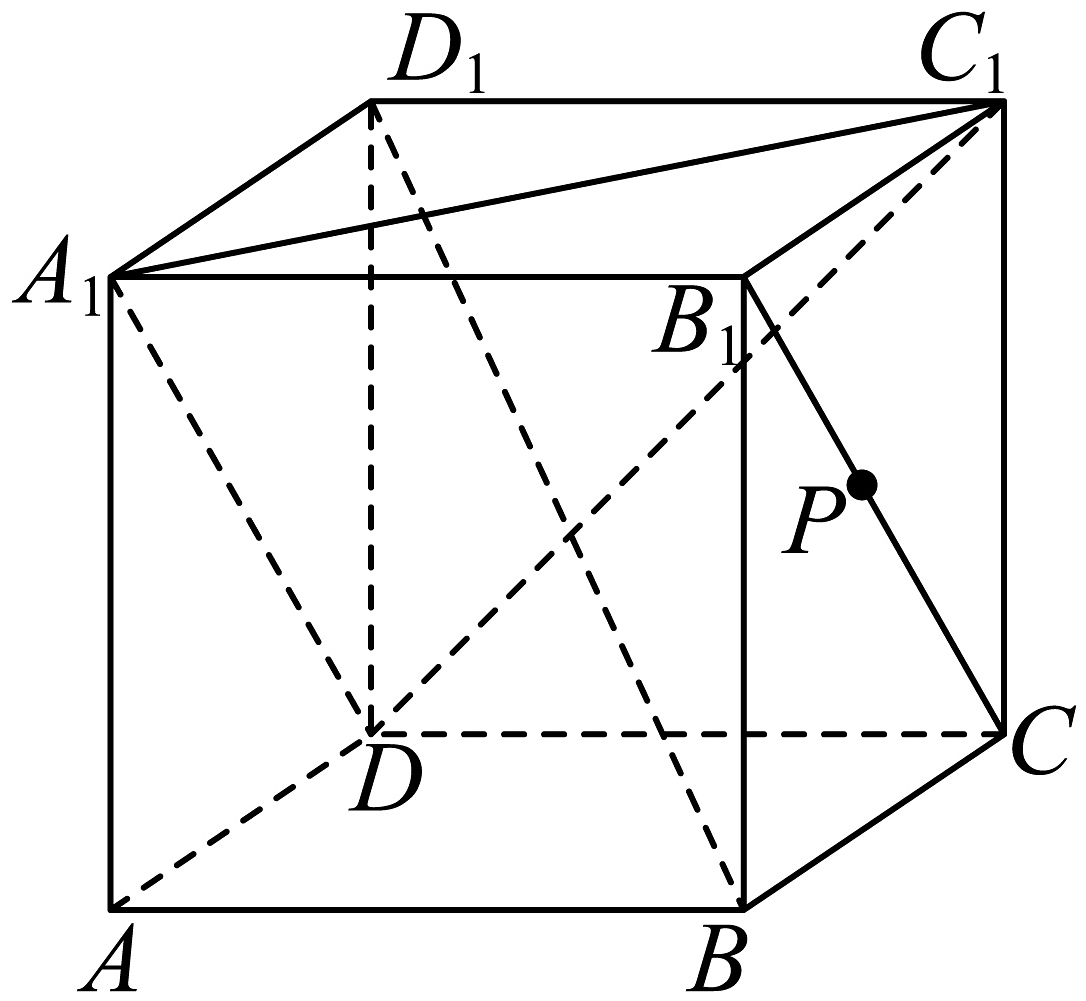A、三棱锥 $P - A_{1} C_{1} D$ 的体积为定值 B、异面直线 $A P$ 与 $A_{1} D$ 所成角的取值范围是 $[\frac{π}{4}, \frac{π}{2}]$ C、平面 $A D P$ 与平面 $A B C D$ 所成夹角的余弦值取值范围是 $[\frac{\sqrt{2}}{2}, 1]$ D、直线 $C_{1} P$ 与平面 $A_{1} C_{1} D$ 所成角的正弦值的最大值为 $\frac{\sqrt{6}}{3}$

查看解析
2、如图，在直三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中， $△ A B C$ 是等边三角形， $A A_{1} = \sqrt{2}$ ， $A B = 2$ ，则点 $C$ 到直线 $A B_{1}$ 的距离为（）

A、 $\frac{\sqrt{6}}{3}$ B、 $\frac{\sqrt{23}}{3}$ C、 $\frac{\sqrt{30}}{3}$ D、 $\frac{\sqrt{15}}{3}$

查看解析
3、已知点 $A (3, 1, 4)$ ，则点 $A$ 关于 $x$ 轴对称的点的坐标为（）

A、 $(3, - 1, - 4)$ B、 $(1, - 3, 4)$ C、 $(- 3, - 1, - 4)$ D、 $(4, - 1, 3)$

查看解析
4、若直线 $a x + y - 2 = 0$ 经过两直线 $5 x - 3 y - 17 = 0$ 和 $x - y - 5 = 0$ 的交点，则 $a =$ （）

A、2 B、4 C、6 D、8

查看解析
5、已知 $P (A) = \frac{1}{4} ， P (B) = \frac{1}{6} ， P (A B) = \frac{1}{12}$ ，则 $P (A \cup B) =$ （）

A、 $\frac{5}{12}$ B、 $\frac{1}{3}$ C、 $\frac{1}{4}$ D、 $\frac{1}{6}$

查看解析
6、向量 $\vec{a} = (x, 1, 3)$ ， $\vec{b} = (2, - y, 6)$ ，若 $\vec{a} / / \vec{b}$ ，则（）

A、 $x = y = 1$ B、 $x = - 1, y = - 2$ C、 $x = 1, y = - 2$ D、 $x = - 1, y = 2$

查看解析
7、已知集合 $A = \{x ∣ x^{2} < 9\}, B = {x ∣ x - 3 \leq 0}$ ，则 $A \cap B =$ （）

A、 ${1, 2}$ B、 ${0, 1, 2}$ C、 ${x ∣ - 3 < x \leq 3}$ D、 ${x ∣ - 3 < x < 3}$

查看解析
8、已知双曲线 $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1, (a > 0, b > 0)$ 的离心率为2，右焦点 $F$ 到渐近线的距离为 $\sqrt{3}$ ．

(1)、求双曲线的标准方程；

(2)、若点 $P$ 为双曲线右支上一动点，过点 $P$ 与双曲线相切的直线 $l$ ，直线 $l$ 与双曲线的渐近线分别交于M，N两点，求 $△ F M N$ 的面积的最小值．

查看解析
9、如图，已知四棱台 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 的上、下底面分别是边长为2和4的正方形，平面 $A A_{1} D_{1} D$ ⊥平面ABCD， $A_{1} A = D_{1} D = \sqrt{17}$ ，点P是棱 $D D_{1}$ 的中点，点Q在棱BC上．

(1)、若 $B Q = 3 Q C$ ，证明： $P Q ∥$ 平面 $A B B_{1} A_{1}$ ；

(2)、若二面角 $P - Q D - C$ 的正弦值为 $\frac{5 \sqrt{26}}{26}$ ，求BQ的长．

查看解析
10、已知函数 $f (x) = a x^{3} + b x^{2} - 3 x$ 在点 $(- 1, f (- 1))$ 处的切线方程为 $y = 2$

(1)、求函数 $f (x)$ 的解析式；

(2)、若 $m \neq - 2$ ，且过点 $(1, m)$ 可作曲线 $y = f (x)$ 的三条切线，求实数 $m$ 的取值范围.

查看解析
11、已知 $|\begin{array}{l} a & c \\ b & d \end{array}| = a d - b c$ ，定义运算@： $f (x) @ g (x) = |\begin{array}{r} a & f^{'} (x) + 1 \\ f (x) & g (x) \end{array}|$ ，其中 $f^{'} (x)$ 是函数 $f (x)$ 的导数.若 $φ (x) = (\ln x) @ (e^{a x} + 1)$ ，设实数 $a > 0$ ，若对任意 $x > 0, φ (x) \geq 0$ 恒成立，则 $a$ 的最小值为（）

A、 $\frac{1}{2 e}$ B、 $\frac{1}{e}$ C、e D、2e

查看解析
12、一个不透明的袋子装有5个完全相同的小球，球上分别标有数字1，2，3，4，4．现甲从中随机摸出一个球记下所标数字后放回，乙再从中随机摸出一个球记下所标数字，若摸出的球上所标数字大即获胜（若所标数字相同则为平局），则在甲获胜的条件下，乙摸到2号球的概率为．

查看解析
13、抛物线 $y = - \frac{1}{2} x^{2}$ 的准线方程是．

查看解析
14、在一个有限样本空间中，假设 $P (A) = P (B) = P (C) = \frac{1}{3}$ ，且A与B相互独立，A与C互斥，则（）

A、 $P (A \cup B) = \frac{2}{3}$ B、 $P (\bar{C} |A) = 2 P (A |\bar{C})$ C、 $P (\bar{C} |A B) = 1$ D、若 $P (C |B) + P (C |\bar{B}) = \frac{1}{2}$ ，则B与C互斥

查看解析
15、已知向量 $\vec{a} = (- 1, 1), \vec{b} = (- 2, 3), \vec{c} = (m, n - 1)$ ，则（）

A、 $| \vec{a} - \vec{b} | = \sqrt{5}$ B、当 $(\vec{a} + \vec{b}) ⊥ \vec{c}$ 时， $4 n - 3 m = 4$ C、当 $\vec{a} / / \vec{c}$ 时， $m - n = 1$ D、 $\vec{a}$ 在 $\vec{b}$ 上的投影向量的坐标为 $(- \frac{10}{13}, \frac{15}{13})$

查看解析
16、在平面直角坐标系 $x O y$ 中，点 $A (- 1, 0), B (2, 3)$ ，向量 $\vec{O C} = m \vec{O A} + n \vec{O B}$ ，且 $m - n - 4 = 0$ .若 $P$ 为椭圆 $x^{2} + \frac{y^{2}}{7} = 1$ 上一点，则 $|\vec{P C}|$ 的最小值为（）

A、 $\frac{4}{5} \sqrt{10}$ B、 $\sqrt{10}$ C、 $\frac{8}{5} \sqrt{10}$ D、 $2 \sqrt{10}$

查看解析
17、已知体积为 $4 \sqrt{3} π$ 的球 $O$ 与正四棱锥的底面和4个侧面均相切，已知正四棱锥的底面边长为 $4 \sqrt{3}$ . 则该正四棱锥体积值是（）

A、 $\frac{128 \sqrt{3}}{3}$ B、 $43 \sqrt{3}$ C、 $96 \sqrt{3}$ D、 $\frac{80 \sqrt{3}}{3}$

查看解析
18、命题“ $\exists x \in [1, 2], x^{2} + \ln x - 2 a \leq 0$ ”为假命题，则实数 $a$ 的取值范围为（）

A、 $(- \infty, \frac{1}{2})$ B、 $(- \infty, 0)$ C、 $(- \infty, \ln 2 + 2)$ D、 $(- \infty, \ln 2 + 4)$

查看解析
19、已知函数 $f (x + 1)$ 的图象关于点 $(1, 1)$ 对称，则下列函数是奇函数的是（）

A、 $y = f (x) + 1$ B、 $y = f (x + 2) + 1$ C、 $y = f (x) - 1$ D、 $y = f (x + 2) - 1$

查看解析
20、在 $(a x - 1) {(2 x - 1)}^{3}$ 的展开式中，若各项系数的和为 $0$ ，则 $x^{3}$ 的系数为（）

A、20 B、 $- 20$ C、30 D、 $- 30$

查看解析

上一页 867 868 869 870 871 下一页跳转