版本：

全部人教A版（2019）人教B版（2019）北师大版（2019）苏教版（2019）上教版（2020）人教新课标A版人教新课标B版苏教版北师大版湘教版沪教版人教版（旧版）

相关试卷

1、已知 $a^{\frac{1}{2}} + a^{- \frac{1}{2}} = 3, a > 1$ ，求下列各式的值：

(1)、 $\frac{a^{2} + a^{- 2} - 1}{a + a^{- 1} - 1}$ ；

(2)、 $\frac{(a^{2} + 1) (a^{- \frac{2}{3}} - a^{- \frac{1}{2}})}{\sqrt{a^{\frac{2}{3}} + a - 2 a^{\frac{5}{6}}}}$ ．

查看解析
2、对于函数 $f (x)$ ，如果存在函数 $g (x) = a x + b (a$ ， $b$ 为常数），使得对于区间 $D$ 上的一切实数 $x$ 都有 $f (x) \leq g (x)$ 成立，则称函数 $g (x)$ 为函数 $f (x)$ 在区间 $D$ 上的一个“覆盖函数”，设 $f (x) = 2^{x}$ ， $g (x) = 2 x$ ，若函数 $g (x)$ 为函数 $f (x)$ 在区间 $[m, n]$ 上的一个“覆盖函数”，则 $2^{| m - n |}$ 的最大值为．

查看解析
3、若 $x^{2} - 3 x + 1 = 0$ ，则 $x^{3} + \frac{1}{x^{3}}$ 的值为.

查看解析
4、若 $a = 27, b = 16$ ， $\frac{(- 2 \sqrt{a b}) \times (- 8 \sqrt[3]{a^{2} b^{5}})}{\sqrt[6]{a^{2} b^{7}} \times 4 \sqrt[4]{a^{2} b^{5}}}$ =

查看解析
5、 ${(5 \frac{1}{16})}^{0.5} - {(2 \frac{10}{27})}^{- \frac{2}{3}} - {(2^{- 1})}^{{(\sqrt{3})}^{2}}$ 的值是

查看解析
6、已知函数 $f (x)$ 满足：① $\forall x$ ， $y \in R$ ， $f (x y) = {[f (x)]}^{y}$ ；② $f (- 2) > 1$ ，则（）

A、 $f (0) = 0$ B、 $f (x + y) = f (x) \cdot f (y)$ C、 $f (x)$ 在 $R$ 上是减函数 D、 $\forall x \in [1, 3]$ ， $f (x^{2} - k x) \cdot f (x - 3) \geq 1$ ，则 $k \geq 3$

查看解析
7、已知函数 $f (x) = 2^{x} - 2^{- x}$ ，若 $x_{1} < 0, x_{1} + x_{2} > 0$ ，则（）

A、 $f (x_{1}) - f (- x_{2}) > 0$ B、 $f (x_{1}) - f (- x_{2}) < 0$ C、 $f (x_{1}) + f (x_{2}) > 0$ D、 $f (x_{1}) + f (x_{2}) < 0$

查看解析
8、下列结论中，不正确的是（）

A、 ${0.2}^{0.2} > {0.3}^{0.2}$ B、 $2^{- \frac{1}{3}} < 3^{- \frac{1}{3}}$ C、 ${0.8}^{- 0.1} > {1.25}^{0.2}$ D、 ${1.7}^{0.3} > {0.9}^{3.1}$

查看解析
9、 $⌈x⌉$ 表示大于或者等于 $x$ 的最小整数， $⌊x⌋$ 表示小于或者等于 $x$ 的最大整数．已知函数 $f (x) = \{\begin{matrix} ⌈x^{2} + 3 a x + a⌉, & x \leq 0 \\ e^{- x}, & x > 0 \end{matrix}$ ，且 $f (x)$ 满足：对 $\forall x_{1}, x_{2} \in R$ 有 $(x_{1} - x_{2}) (f (x_{1}) - f (x_{2})) \leq 0$ ，则 $a$ 的可能取值是（）

A、 $- \frac{1}{9}$ B、0 C、 $\frac{1}{3}$ D、 $\frac{4}{9}$

查看解析
10、已知奇函数 $f (x) = a^{x} - b \cdot a^{- x} (a > 0, a \neq 1)$ 在 $[- 1, 1]$ 上的最大值为 $\frac{8}{3}$ ，则 $a =$ （）

A、 $\frac{1}{3}$ 或3 B、 $\frac{1}{2}$ 或2 C、3 D、2

查看解析
11、设 $a = {(\frac{2}{3})}^{\frac{1}{3}}$ ， $b = {1.5}^{- 0.2}$ ， $c = {0.8}^{0.2}$ ，则（）

A、 $a < c < b$ B、 $c < a < b$ C、 $b < c < a$ D、 $a < b < c$

查看解析
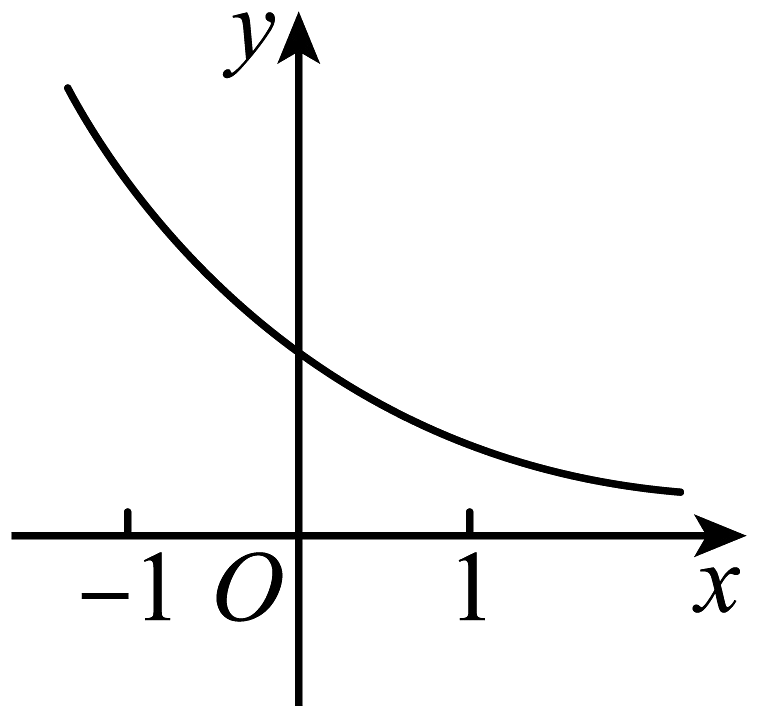
12、已知指数函数 $y = {(\frac{b}{a})}^{x}$ 的图象如图所示，则一次函数 $y = a x + b$ 的图象可能是（       ）


A、    B、    C、    D、

查看解析
13、已知函数 $f (x) = \frac{2^{x} - 1}{2^{x} + 1} + a x^{2023} - \frac{b}{x} - 6$ ， $f (- 2023) = 5$ ，则 $f (2023) =$ （）

A、12 B、 $- 12$ C、 $- 17$ D、17

查看解析
14、已知幂函数 $f (x) = (a^{2} - a - 1) x^{a}$ 在区间 $(0, + \infty)$ 上单调递增，则函数 $g (x) = b^{x + a} - 1 (b > 1)$ 的图象过定点（）

A、 $(- 2, 0)$ B、 $(0, - 2)$ C、 $(2, 0)$ D、 $(0, 2)$

查看解析
15、下列根式与分数指数幂的互化错误的是（）

A、 $\sqrt[3]{a \sqrt{a}} = a^{\frac{1}{2}} (a > 0)$ B、 $x^{- \frac{3}{4}} = - \sqrt[4]{x^{3}} (x > 0)$ C、 $x^{- \frac{1}{2}} y^{\frac{2}{3}} = \frac{\sqrt[3]{y^{2}}}{\sqrt{x}} (x > 0, y > 0)$ D、 ${[\sqrt[3]{{(- x)}^{2}}]}^{\frac{3}{4}} = x^{\frac{1}{2}} (x > 0)$

查看解析
16、设全集为 $R$ ，集合 $A = {x | 0 < x < 2}$ ， $B = {x | 2^{x - 1} \geq 1}$ ，则 $A \cap (C_{R} B) =$

A、 ${x | 0 < x \leq 1}$ B、 ${x | 0 < x < 1}$ C、 ${x | 1 \leq x < 2}$ D、 ${x | 0 < x < 2}$

查看解析
17、已知函数 $f (x) = \frac{2^{x} - a}{2^{x} + 1}$ 为定义在R上的奇函数.

(1)、求a的值；

(2)、判断函数 $f (x)$ 的单调性，并用单调性定义证明；

(3)、若关于x的不等式 $f (f (x)) + f (t) < 0$ 有解，求t的取值范围.

查看解析
18、设集合 $A = \{x |- 1 \leq x + 1 \leq 6\}$ ， $B = \{x |m - 1 < x < 2 m + 1\}$ ．

(1)、当 $m = 3$ 时，求 $A \cap B$ 与 $A \cup B$ ；

(2)、当 $B \subseteq A$ 时，求实数 $m$ 的取值范围．

查看解析
19、回答下列问题

(1)、解一元二次不等式 $x^{2} + 2 x - 15 > 0$ ；

(2)、已知不等式 $m x^{2} - m x + 2 > 0$ ，当 $x \in R$ 时不等式恒成立，求实数 $m$ 的取值范围；

查看解析
20、回答下列问题

(1)、当 $x > 5$ 时，求 $f (x) = x + \frac{6}{x - 5}$ 的最小值

(2)、若 $x > 0, y > 0$ ，且 $\frac{2}{x} + \frac{8}{y} = 1$ ，求 $x + y$ 的最小值．

查看解析

上一页 869 870 871 872 873 下一页跳转