相关试卷
-
1、一个袋子中装有大小和质地相同的4个球,其中有2个红球(标号为1和2),2个白球(标号为3和4),甲、乙两人先后从袋中不放回地各摸出1个球.设“甲摸到红球”为事件 , “乙摸到红球”为事件.(1)、小明同学认为:由于甲先摸球,所以事件发生的可能性大于发生的可能性.小明的判断是否正确,请说明理由;(2)、判断事件与是否相互独立,并证明.
-
2、如图,已知正三棱锥的侧棱长为2024,过其底面中心作动平面 , 交线段PC于点 , 交PA,PB的延长线于M,N两点.则.

-
3、已知 , 若的平分线方程为 , 则所在的直线方程为 .
-
4、如图,在正三棱柱中, , 点满足 , 则下列说法正确的有( )
 A、当 , , 时,对任意的点 , 都有三棱锥的体积为定值 B、当 , , 时,存在点 , 使得 C、当 , , 时,存在唯一点 , 使得 D、当时,的最小值是
A、当 , , 时,对任意的点 , 都有三棱锥的体积为定值 B、当 , , 时,存在点 , 使得 C、当 , , 时,存在唯一点 , 使得 D、当时,的最小值是 -
5、如图为2022年全国居民消费价格月度涨跌幅情况,则( )
 A、环比涨跌幅的极差小于同比涨跌幅的极差 B、环比涨跌幅的平均数为0.1% C、环比涨跌幅的方差小于同比涨跌幅的方差 D、同比涨跌幅的上四分位数为1.55%
A、环比涨跌幅的极差小于同比涨跌幅的极差 B、环比涨跌幅的平均数为0.1% C、环比涨跌幅的方差小于同比涨跌幅的方差 D、同比涨跌幅的上四分位数为1.55% -
6、直线的方程为 , 若在轴上的截距为 , 且.则下列说法正确的是( )A、直线与的交点坐标为 , 直线在轴上的截距是 B、已知直线经过与的交点,且在轴上的截距是在轴上的截距的2倍,的方程为 C、已知动直线经过与的交点,当原点到距离最大时,到距离为 D、直线 , , 若 , 则或2
-
7、已知 , 都是正实数,且直线与直线互相垂直,则的最小值为( )A、12 B、10 C、8 D、25
-
8、在空间中,“经过点 , 法向量为的平面的方程(即平面上任意一点的坐标满足的关系)是:”.如果给出平面的方程是 , 平面的方程是 , 则由这两平面所成的角的正弦值是( )A、 B、 C、 D、
-
9、在四棱柱中,平面 , 底面是边长为1的正方形,侧棱的长为 , 为侧棱上的动点(包括端点),则( )
 A、对任意的 , 存在点 , 使得 B、当且仅当时,存在点 , 使得 C、当且仅当时,存在点 , 使得 D、当且仅当时,存在点 , 使得
A、对任意的 , 存在点 , 使得 B、当且仅当时,存在点 , 使得 C、当且仅当时,存在点 , 使得 D、当且仅当时,存在点 , 使得 -
10、如图,在直三棱柱中, , 则异面直线与所成角的余弦值等于( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
11、某校高三(1)班(45人)和高三(2)班(30人)进行比赛,按照分层抽样的方法从两个班共抽取10名同学,相关统计情况如下:高三(1)班答对题目的平均数为 , 方差为;高三(2)班答对题目的平均数为 , 方差为 , 则这10人答对题目的方差为( )A、 B、 C、 D、
-
12、如图1,已知圆心在轴的圆经过点和.过原点且不与铀重合的直线与圆交于A、B两点(在轴上方).
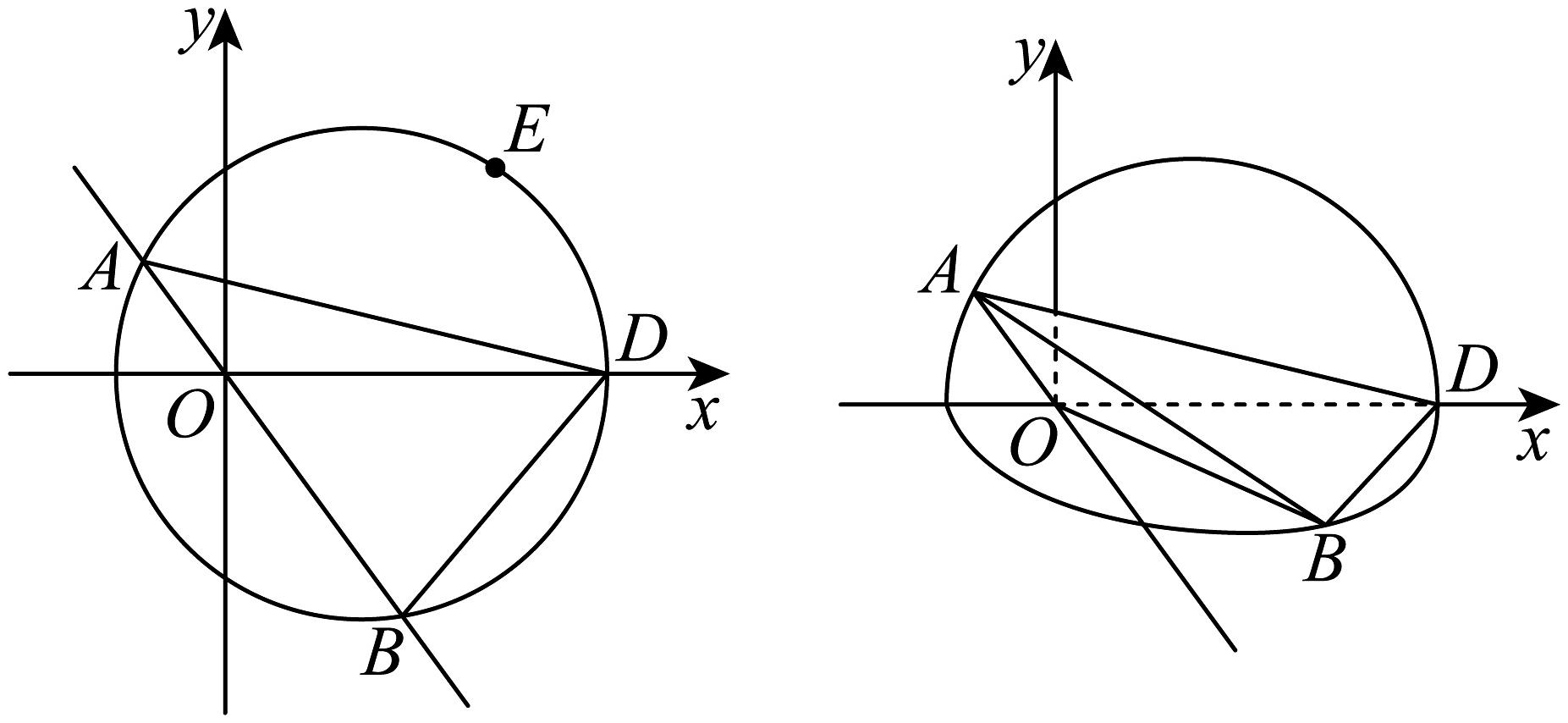 (1)、求圆的标准方程;(2)、若的面积为 , 求直线l的方程;(3)、将平面xOy沿轴折叠,使轴正半轴和轴所确定的半平面(平面AOD)与y轴负半轴和轴所确定的半平面(平面BOD)互相垂直,如图2,求折叠后的范围.
(1)、求圆的标准方程;(2)、若的面积为 , 求直线l的方程;(3)、将平面xOy沿轴折叠,使轴正半轴和轴所确定的半平面(平面AOD)与y轴负半轴和轴所确定的半平面(平面BOD)互相垂直,如图2,求折叠后的范围. -
13、已知圆 , 点在圆上,过作轴的垂线,垂足为 , 动点P满足 , 设动点的轨迹为曲线.(1)、求曲线的方程;(2)、斜率存在且不过的直线l与曲线C相交于M、N两点,BM与BN的斜率之积为.
①证明:直线l过定点;
②求面积的最大值.
-
14、已知向量 , , 若 , 则( )A、 B、1 C、 D、
-
15、中国南宋大数学家秦九韶提出了“三斜求积术”,即已知三角形三边长求三角形面积的公式:设三角形的三条边长分别为 , , , 则三角形的面积可由公式求得,其中为三角形周长的一半,这个公式也被称为海伦-秦九韶公式.现有一个三角形的边长满足 , , 则此三角形面积的最大值为( )A、 B、 C、 D、
-
16、如图,已知向量 , 可构成空间向量的一个基底,若 , 在向量已有的运算法则的基础上,新定义一种运算 , 显然的结果仍为一向量,记作 .
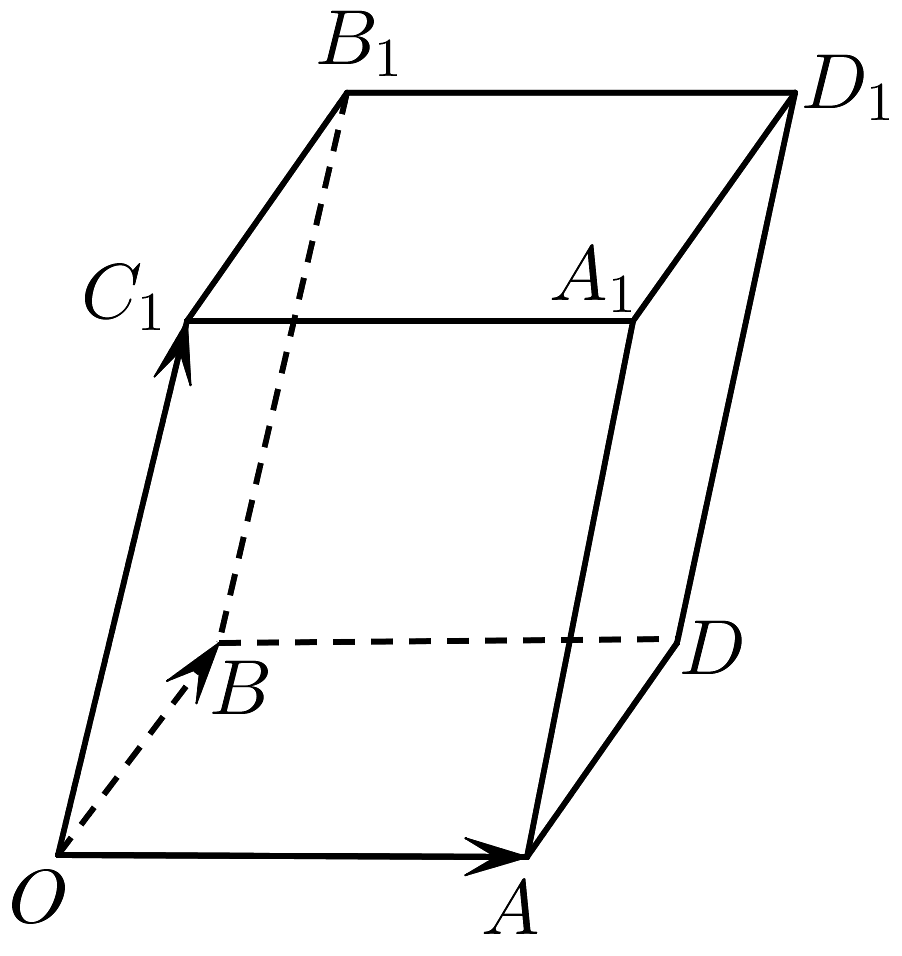
(1)求证:向量为平面的法向量;
(2)求证:以为边的平行四边形的面积等于;
(3)将四边形按向量平移,得到一个平行六面体 , 试判断平行六面体的体积与的大小.
-
17、如图,在三棱柱中,是边长为4的等边三角形,是的中点, .
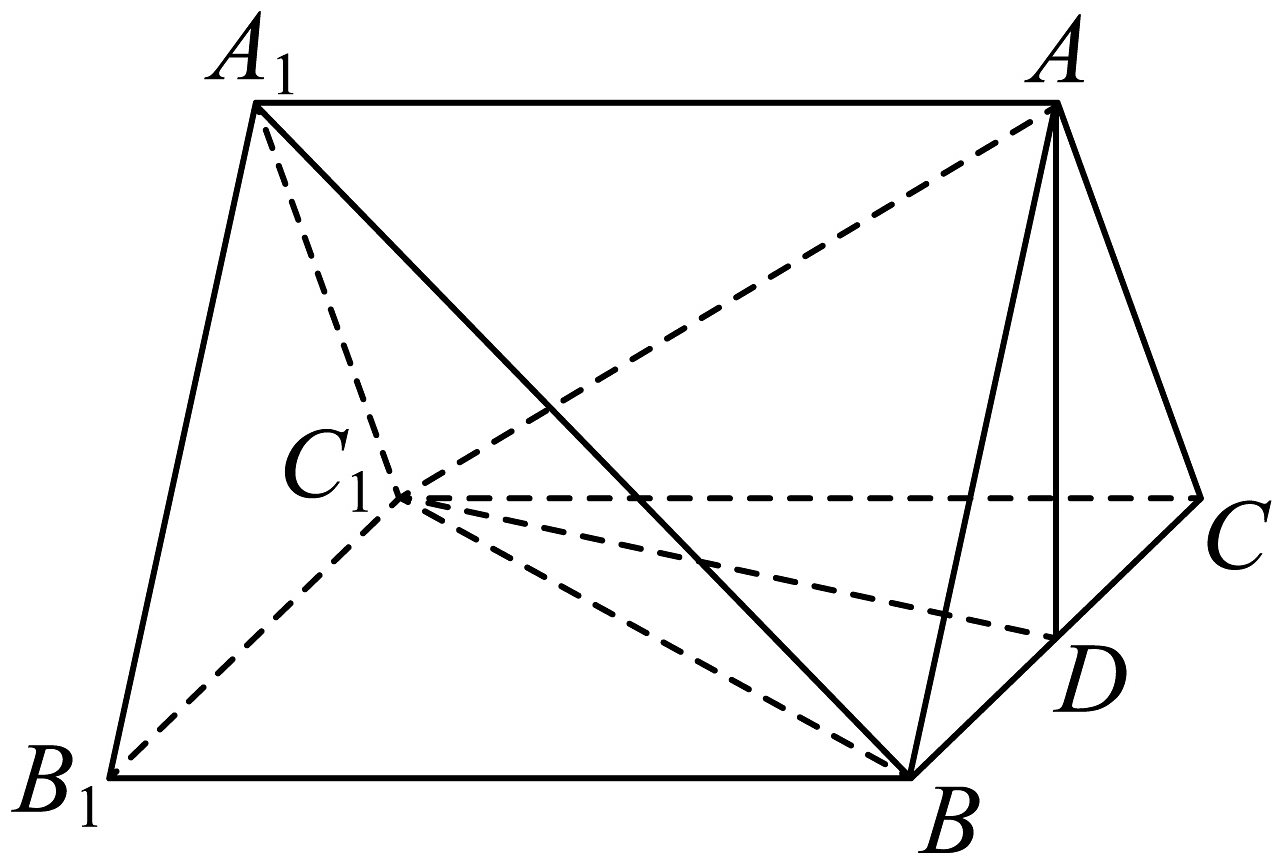 (1)、求证:平面;(2)、当三棱柱的体积最大时,求直线到平面的距离.
(1)、求证:平面;(2)、当三棱柱的体积最大时,求直线到平面的距离. -
18、2022年卡塔尔世界杯足球赛于11月21日至12月18日在卡塔尔境内举办,这是第二十二届世界杯足球赛,是历史上首次在卡塔尔和中东国家境内举行,也是继2002年韩日世界杯之后时隔二十年第二次在亚洲举行的世界杯足球赛,备受瞩目,一时间掀起了国内外的足球热潮,某机构为了解球迷对足球的喜爱,为此进行了调查.现从球迷中随机选出100人作为样本,并将这100人按年龄分组:第1组 , 第2组 , 第3组 , 第4组第5组 , 得到的频率分布直方图如图所示.
 (1)、求样本中数据的第百分位数;(2)、求样本数据的平均数;(3)、若将频率视为概率,现在要从和两组中用分层抽样的方法抽取6人,再从这6人中随机抽取2人进行座谈,求抽取的2人中至少有1人的年龄在组的概率.
(1)、求样本中数据的第百分位数;(2)、求样本数据的平均数;(3)、若将频率视为概率,现在要从和两组中用分层抽样的方法抽取6人,再从这6人中随机抽取2人进行座谈,求抽取的2人中至少有1人的年龄在组的概率. -
19、已知向量 .(1)、若 , 求实数;(2)、若向量与所成角为钝角,求实数的范围.
-
20、如图,边长为1的正方形ABCD所在平面与正方形ABEF所在平面互相垂直,动点M,N分别在正方形对角线AC和BF上移动,且CM=BN=a(0<a<).则下列结论:
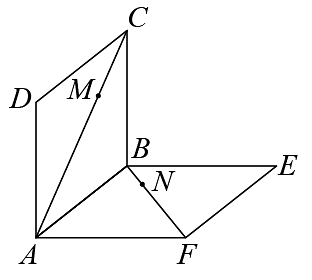
①当a=时,ME与CN相交;
②MN始终与平面BCE平行;
③异面直线AC与BF所成的角为45°;
④MN的最小值为 .
正确的序号是 .