相关试卷
-
1、设平面与长方体的六个面的夹角分别为 , 则的值为( )A、2 B、3 C、4 D、6
-
2、某学校有、两家餐厅,王同学第1天午餐时随机选择一家餐厅用餐.如果第1天去餐厅,那么第2天去餐厅的概率为0.6;如果第1天去B餐厅,那么第2天去餐厅的概率为0.8,则王同学第2天去A餐厅用餐的概率为( )A、0.7 B、0.6 C、0.5 D、0.4
-
3、在中,为边上的中线, , , 则的值为( )A、 B、 C、 D、
-
4、设复数 , 是虚数单位,则( )A、 B、 C、 D、2
-
5、若连续函数满足在定义域内恒成立,则称为“T函数”.(1)、判断以下函数是否为“T函数”,请说明理由.
(ⅰ);
(ⅱ);
(ⅲ).
(2)、若非常值函数存在二阶导数,证明:为“T函数”的充要条件是为常值函数.(3)、已知非常值函数为“T函数”,且.记为不超过x的最大整数,讨论函数在区间上的单调性. -
6、在一个不透明的袋子中放有n个除颜色外完全相同的小球,其中有m个红色球与个白色球(满足且n,).现设计如下试验流程:每次从袋中随机摸取一球,若为红色球则定义为“成功”事件,每次“成功”后将对应红球永久移除;若抽取为白色球则将其放回袋中并重新摇匀,试验持续至袋中无红色球时终止.(1)、当 , 时,求前两次摸取过程中恰发生一次“成功”事件的概率;(2)、设 , 若第X次摸取时试验首次出现“成功”事件,记随机变量X的数学期望为 , 试比较与的大小;(3)、基于随机变量可加性原理 , 当 , 时,设试验终止时的累计抽取次数为.证明:.
-
7、如图,椭圆C:的离心率为 , 左右焦点分别为 , , 左右顶点分别为A,B,椭圆上有一动点D(异于A,B),点E为线段的中点,点O为坐标原点.直线与直线相交于点M.已知面积有最大值为.
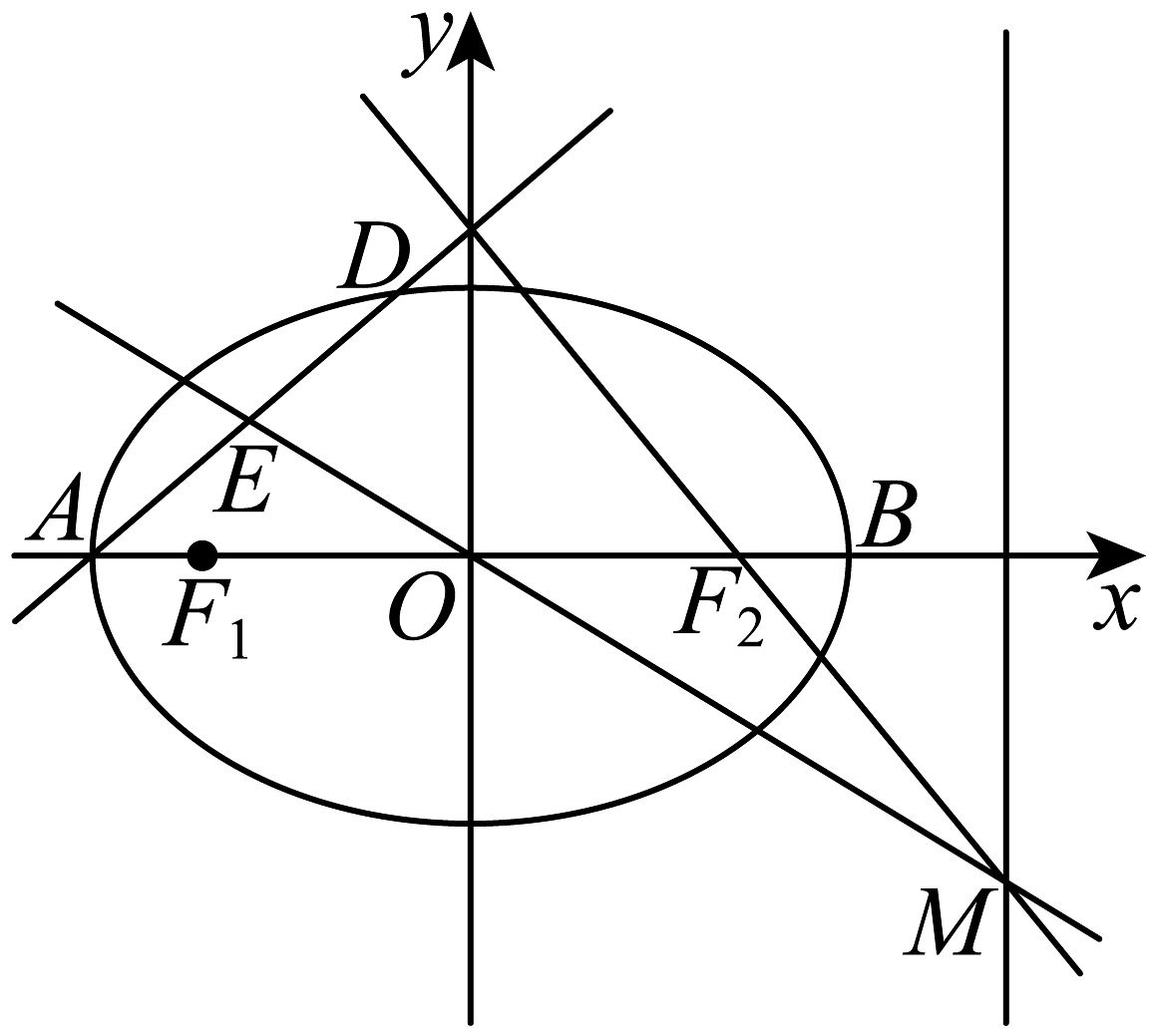 (1)、当点M坐标为时,求;(2)、证明:.
(1)、当点M坐标为时,求;(2)、证明:. -
8、如图,已知四棱台的体积为 , 底面为等腰梯形, , , , 平面 , 且与相交于点E.
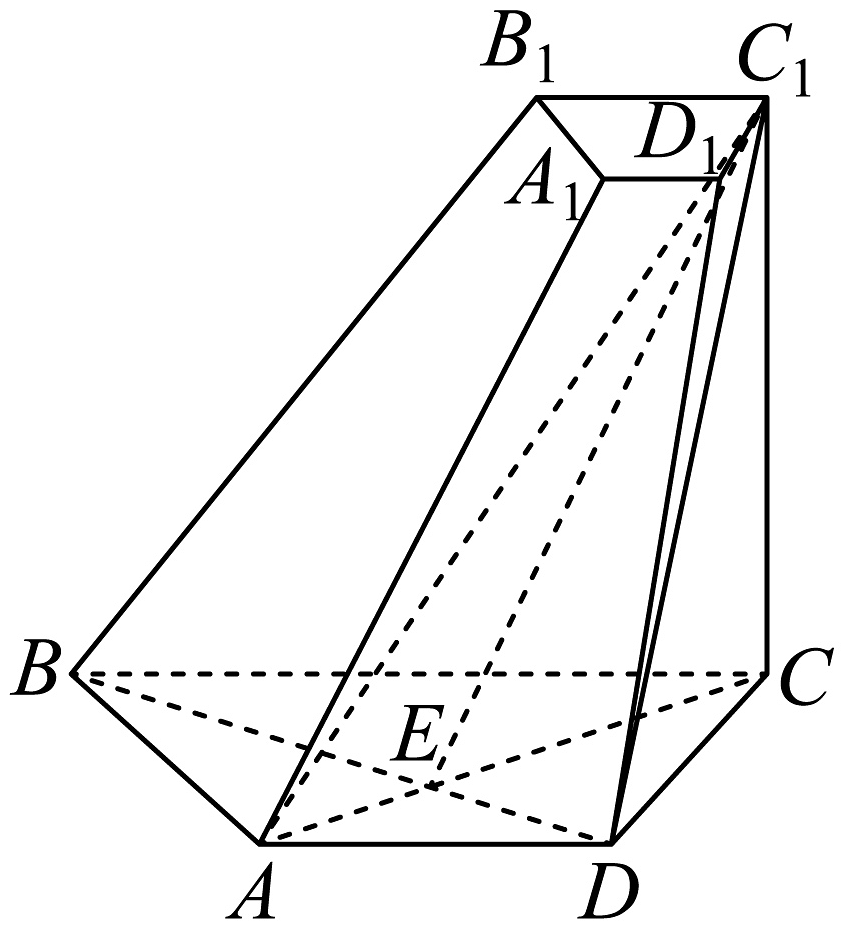 (1)、证明:;(2)、求平面与平面的夹角的余弦值.
(1)、证明:;(2)、求平面与平面的夹角的余弦值. -
9、已知在中,角A,B,C所对的边记为a,b,c,设其外心为O.若.(1)、求角A的大小;(2)、若 , 求的面积.
-
10、圆台内有一个球,与圆台的上下底面及所有母线均相切,则圆台与球的体积比的取值范围为.
-
11、设直线与抛物线C:相交于点A,B,点F为抛物线C的焦点.若 , 则点F的坐标为.
-
12、已知函数为奇函数,则.
-
13、如图所示,某游戏闯关者需从区域Ⅰ内的定点P快速移动至区域Ⅱ内的定点Q.两区域以直线l为分界线,已知P,Q两点到直线l的距离分别为1,2,且向量在直线l的方向向量上的投影向量的模长为3,考虑到两区域通行环境差异,设定闯关者在区域Ⅰ的移动速率为a,在区域Ⅱ中的移动速率为b,线段与直线l相交于点A,若图示折线路径是耗时最短的闯关路线.则下列说法正确的有( )
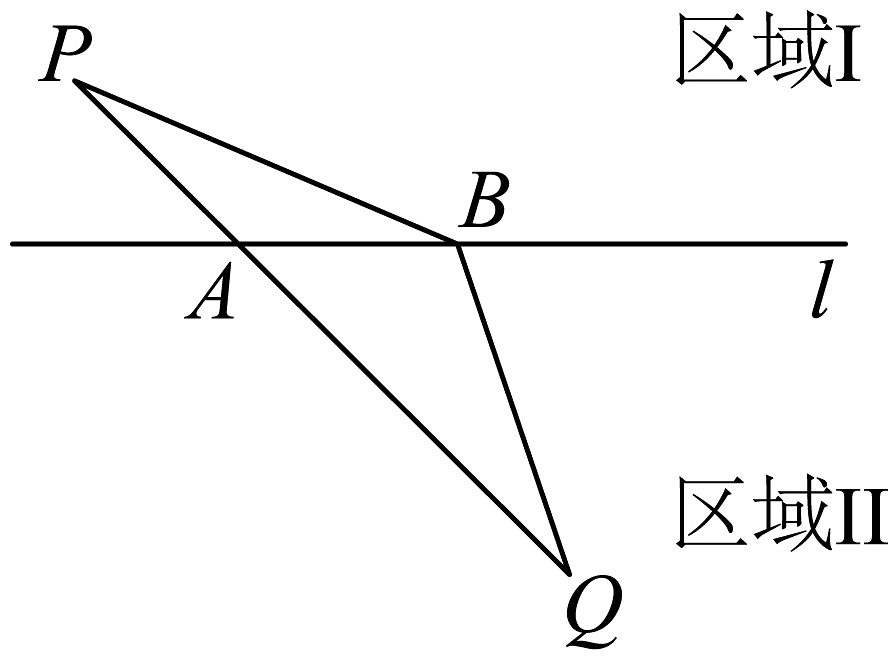 A、存在实数 , 使得 B、若 , 则 C、 D、
A、存在实数 , 使得 B、若 , 则 C、 D、 -
14、已知定义在上的可导函数满足: , 若单调递增数列满足:则( )A、的通项公式是 B、函数是增函数 C、可能是等比数列 D、若 , 则
-
15、已知为锐角,若 , 则下列说法正确的有( )A、的终边经过点 B、 C、 D、若 , 则
-
16、若数轴上有一个质点位于处,每次运动它都等可能地向左或向右移动一个单位,已知它在第10次运动后首次到达处,则它在运动过程中没有重返过原点的概率为( )A、 B、 C、 D、
-
17、已知A,B,C是函数图象上的三点,A在x轴上,且轴,若 , 则的值为( )A、0 B、-1 C、-107 D、82
-
18、在棱长为1的正方体中,点P,Q分别为棱 , 上的动点(可与端点重合),若面 , 则线段的长度为( )A、 B、 C、 D、
-
19、如图是函数的图象,则的值为( )
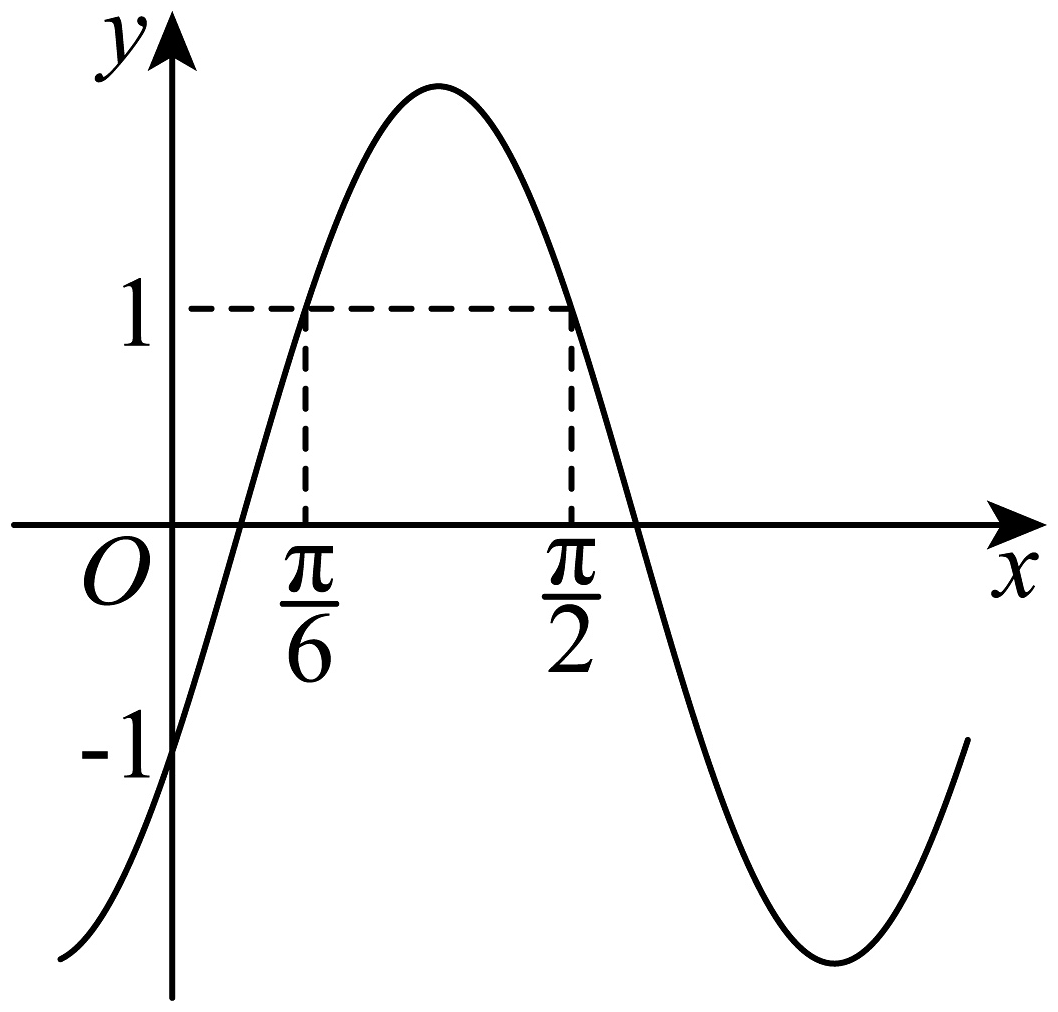 A、 B、1 C、2 D、3
A、 B、1 C、2 D、3 -
20、设 , 则的值为( )A、20 B、-20 C、160 D、-160