相关试卷
-
1、已知为锐角,若 , 则下列说法正确的有( )A、的终边经过点 B、 C、 D、若 , 则
-
2、若数轴上有一个质点位于处,每次运动它都等可能地向左或向右移动一个单位,已知它在第10次运动后首次到达处,则它在运动过程中没有重返过原点的概率为( )A、 B、 C、 D、
-
3、已知A,B,C是函数图象上的三点,A在x轴上,且轴,若 , 则的值为( )A、0 B、-1 C、-107 D、82
-
4、在棱长为1的正方体中,点P,Q分别为棱 , 上的动点(可与端点重合),若面 , 则线段的长度为( )A、 B、 C、 D、
-
5、如图是函数的图象,则的值为( )
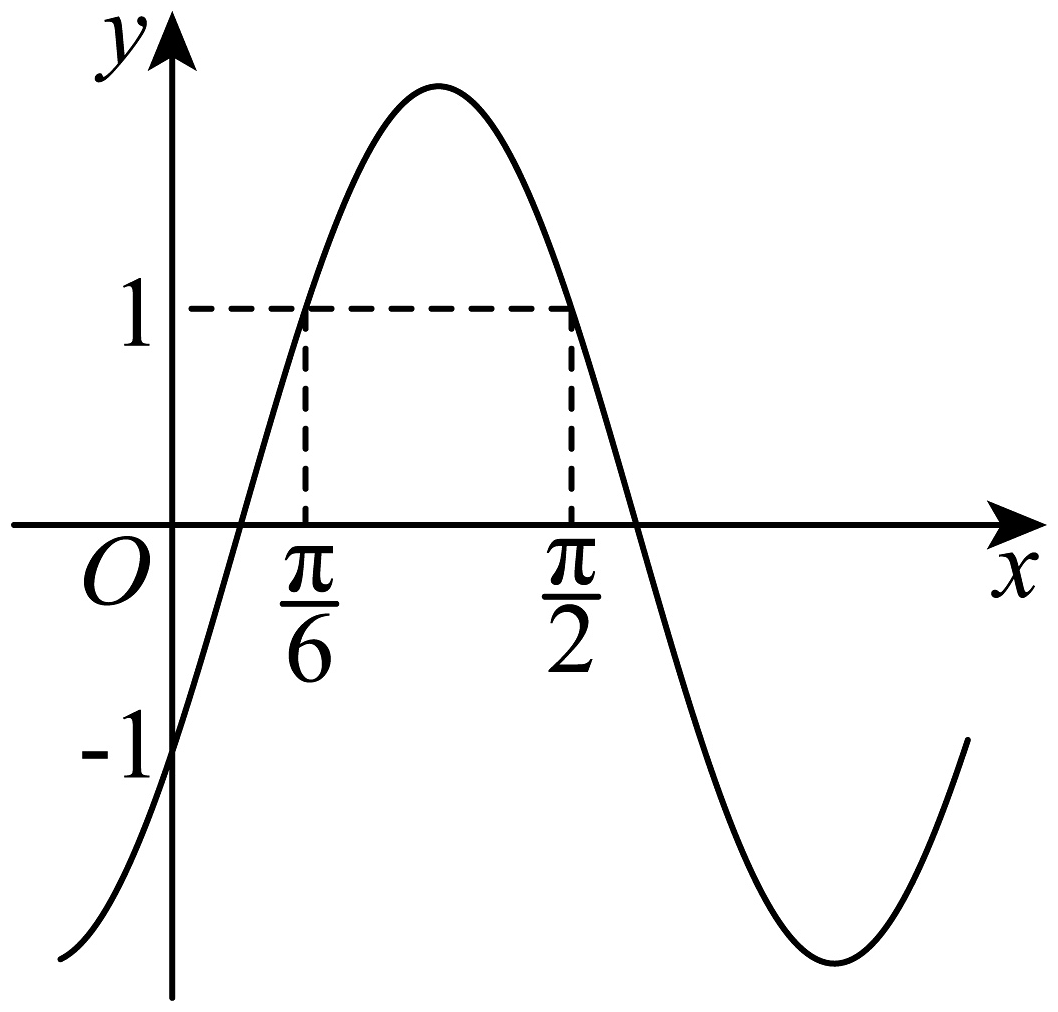 A、 B、1 C、2 D、3
A、 B、1 C、2 D、3 -
6、设 , 则的值为( )A、20 B、-20 C、160 D、-160
-
7、设等差数列的前项和为 , 已知 , , 则( )A、17 B、21 C、23 D、27
-
8、若复数z满足 , 则( )A、 B、 C、 D、
-
9、已知集合 , , 则( )A、 B、 C、 D、
-
10、已知函数.
(1)若函数在定义域内是增函数,求实数的取值范围;
(2)当时,讨论方程根的个数.
-
11、设是等差数列,是等比数列,满足 , , 且 , .(1)、求与的通项公式;(2)、设 , 在平面直角坐标系中,依次连接点 , , , 得到折线 , 求由该折线与直线 , , 所围成的区域的面积 .
-
12、已知数列的前项和为 , 且 .(1)、求数列的通项公式;(2)、设 , , 求使成立的最小的正整数的值.
-
13、已知函数的图象在点处的切线方程是 .(1)、求 , 的值;(2)、求函数的单调区间.
-
14、若函数有两个极值点,则的取值范围为
-
15、甲、乙、丙、丁、戊5名同学站成一排参加文艺汇演,若甲不站在两端,丙和丁相邻,则不同的排列方式共有种.(请用数字作答)
-
16、数列满足 , 且对任意的都有 , 则 .
-
17、定义:设为三次函数,是的导函数,是的导函数,若方程有实数解 , 则称点为三次函数图象的“拐点”.经过探究发现:任意三次函数图象的“拐点”是其对称中心.已知三次函数的极大值点和极小值点分别为 , , 且有 , 则下列说法中正确的是( )A、 , B、方程有三个根 C、若关于的方程在区间上有两解,则或 D、函数图象的对称中心为
-
18、已知的展开式的第2项与第3项系数的和为3,则( )A、 B、展开式的各项系数的和为 C、展开式中奇数项的二项式系数的和为128 D、展开式的常数项为第5项
-
19、定义在上的函数的导函数的图象如图所示,则下列结论正确的是( )
 A、函数在上单调递减 B、函数在上单调递减 C、函数在处取得最小值 D、函数在处取得极大值
A、函数在上单调递减 B、函数在上单调递减 C、函数在处取得最小值 D、函数在处取得极大值 -
20、南北朝时期的著作《孙子算经》中,对同余除法有较深的研究.设、、为整数,若和被除得余数相同,则称和对模同余,记为 . 已知 , 若 , , 则的值可以是( )A、 B、 C、 D、