-
1、已知关于x的一元二次不等式的解集为或 , 则下列说法正确的是( )A、 B、不等式的解集为 C、不等式的解集为 D、
-
2、下列命题正确的是( )A、命题“”的否定是“” B、“”是“”的充分必要条件 C、设 , 若 , 则实数a的值可以是0 D、“”是“”的必要不充分条件
-
3、若集合 , 则下列结论正确的是( )A、 B、 C、 D、
-
4、已知函数 , 则( )A、2 B、 C、 D、5
-
5、若幂函数的图象过点 , 则该幂函数的解析式是( )A、 B、 C、 D、
-
6、(1)已知且 , 求使不等式恒成立的实数的取值范围.
(2)已知 , 且 , 求的最小值.
-
7、如果 , 那么下列不等式不正确的是( )A、 B、 C、 D、
-
8、已知函数 , 则不等式的解集为( )A、 B、 C、 D、
-
9、函数的图象大致是( )A、
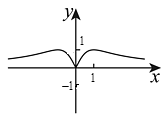 B、
B、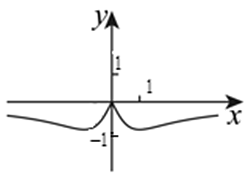 C、
C、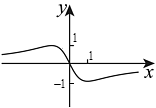 D、
D、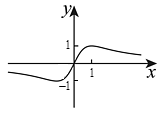
-
10、函数为定义在上的减函数,若 , 则( )A、 B、 C、 D、
-
11、汽车经过启动、加速行驶、匀速行驶、减速行驶之后停车,若把这一过程中汽车的行驶路程s看作时间t的函数,其图象可能是( )A、
 B、
B、 C、
C、 D、
D、
-
12、“”是“”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件
-
13、设全集 , 则( )A、 B、 C、 D、
-
14、已知函数(1)、当时,根据定义证明函数在上单调递增.(2)、若有最小值4,求的值.
-
15、如果 , 则的取值范围为.
-
16、某校“五一田径运动会”上,共有12名同学参加100米、400米、1500米三个项目,其中有8人参加“100米比赛”,有7人参加“400米比赛”,有5人参加“1500米比赛”,“100米和400米”都参加的有4人,“100米和1500米”都参加的有3人,“400米和1500米”都参加的有3人,则下列说法正确的是( )A、三项比赛都参加的有2人 B、只参加100米比赛的有3人 C、只参加400米比赛的有3人 D、只参加1500米比赛的有3人
-
17、已知函数是上的增函数,则实数的取值范围为( )A、 B、 C、 D、
-
18、已知是偶函数,则( )A、 B、 C、1 D、2
-
19、不等式的解集为 , 则函数的图象大致为( )A、
 B、
B、 C、
C、 D、
D、
-
20、若函数的定义域是 , 则函数的定义域为( )A、 B、 C、 D、