-
1、已知动点M到定点的距离比点M到定直线的距离小1,直线交曲线C于A,B两点.(点A在第一象限)(1)、求点M的轨迹C的方程;(2)、若过且与垂直的直线与曲线C交于C,D两点:(点C在第一象限)
(i)求四边形面积的最小值.
(i i)设 , 的中点分别为P,Q,求证:直线过定点.
-
2、已知函数 , .(1)、当时,求曲线在点处的切线方程;(2)、设函数 , 讨论的单调性.
-
3、中,是上的点,平分 , 面积是面积的2倍.(1)、求;(2)、若 , , 求和的长.
-
4、一个三位数的百位、十位、个位上的数字依次为a,b,c.三位数中,当且仅当有两个数字的和等于第三个数字时称为“有缘数”(如213,134等)若a,b, , 且a,b,c互不相同,则这个三位数为“有缘数”共个.
-
5、已知函数H(x) , 下列说法正确的有( )A、若m=0,a=1,则函数H(x)有最大值 B、若m=1,a≠0,则过原点恰好可以作一条直线与曲线y=H(x)相切 C、若a=0,且对任意m∈R,H(x)>0恒成立,则0≤x≤1 D、若对任意m∈R,任意x>0,H(x)≥0恒成立,则a的最小值是
-
6、设离散型随机变量X的分布列如下表;
X
1
2
3
4
5
P
m
0.1
0.3
n
0.3
若离散型随机变量 , 且 , 则正确的是( )
A、 B、 C、 D、 -
7、在中, , 若一个椭圆经过A、B两点,它的一个焦点为点C,另一个焦点在边AB上,则这个椭圆的离心率为( )A、 B、 C、 D、
-
8、函数与的图象的交点个数为( )A、1 B、2 C、3 D、4
-
9、如图,在梯形中,在线段上,.若 , 则( )
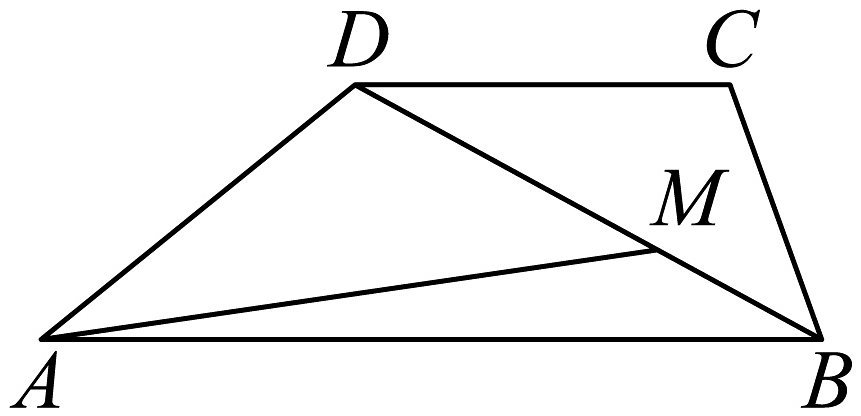 A、 B、 C、 D、
A、 B、 C、 D、 -
10、若函数的定义域为 , 值域为则实数的取值范围为( )A、 B、 C、 D、
-
11、复数的虚部是( )A、 B、 C、 D、
-
12、若复数满足 , 则下列命题正确的有( )A、的虚部是-1 B、 C、 D、是方程的一个根
-
13、某同学参加学校组织的数学知识竞赛,在5道四选一的单选题中有3道有思路,有2道完全没有思路,有思路的题目每道做对的概率为 , 没有思路的题目只好任意猜一个答案.若从这5道题目中任选2题,则该同学2道题目都做对的概率为( )A、 B、 C、 D、
-
14、抛物线有如下光学性质:平行于抛物线对称轴的光线,经过抛物线上的一点反射后,反射光线经过抛物线的焦点.过点且平行于轴的一条光线射向抛物线上的点,经过反射后的反射光线与相交于点 , 则( )A、 B、9 C、36 D、
-
15、若 , 则( )A、 B、 C、 D、
-
16、已知集合 , 集合 , 则如图中的阴影部分表示( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
17、已知函数.(1)、讨论的单调性;(2)、若关于的不等式无整数解,求的取值范围.
-
18、欧几里得生活的时期人们就发现了椭圆有如下的光学性质:由椭圆一焦点射出的光线经椭圆内壁反射后必经过另一焦点现有一椭圆 , 长轴长为 , 从一个焦点发出的一条光线经椭圆内壁上一点反射之后恰好与轴垂直,且 .(1)、求椭圆的标准方程;(2)、已知为该椭圆的左顶点,若斜率为且不经过点的直线与椭圆交于 , 两点,记直线 , 的斜率分别为 , 且满足 .
①证明:直线过定点;
②若 , 求的值.
-
19、如图,在三棱柱中, , , 四边形是菱形.
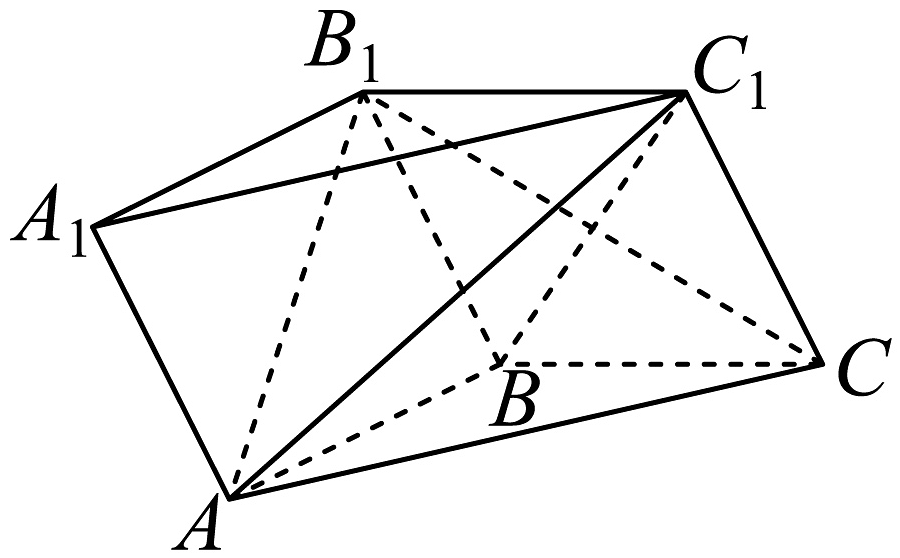 (1)、证明:;(2)、若 , 求二面角的正弦值.
(1)、证明:;(2)、若 , 求二面角的正弦值. -
20、某大型公司进行了新员工的招聘,共有10000人参与.招聘规则为:前两关中的每一关最多可参与两次测试,只要有一次通过,就自动进入下一关的测试,否则过关失败.若连续通过三关且第三关一次性通过,则成功竞聘,已知各关通过与否相互独立.(1)、若小李在第一关、第二关及第三关通过测试的概率分别为 , 求小李成功竞聘的概率;(2)、统计得10000名竞聘者的得分 , 试估计得分在442分以上的竞聘者有多少人.(四舍五人取整)
附:若随机变量 , 则