-
1、已知曲线 , 则该曲线在处的切线方程为
-
2、已知抛物线上一点到焦点 F 的距离为2,又过点 F 的直线交抛物线 C 于 A,B 两点,则下列说法正确的是( )A、抛物线C方程为: B、设 , 则周长的最小值为 C、若 , 则直线AB的倾斜角为 D、x 轴上存在一点N,使为定值
-
3、南宋数学家杨辉所著的《详解九章算法·商功》中出现了如图所示的形状,后人称为“三角垛”,“三角垛”的最上层有个球,第二层有个球,第三层有个球,…,设各层球数构成一个数列 , 且 , 数列的前项和为 , 则正确的选项是( ).
 A、 B、 C、 D、
A、 B、 C、 D、 -
4、某次数学考试后,为分析学生的学习情况,某校从某年级中随机抽取了100名学生的成绩,整理得到如图所示的频率分布直方图.则( )
 A、估计该年级学生成绩的众数为75 B、 C、估计该年级学生成绩的75百分位数约为85 D、估计该年级成绩在80分及以上的学生成绩的平均数为87.50
A、估计该年级学生成绩的众数为75 B、 C、估计该年级学生成绩的75百分位数约为85 D、估计该年级成绩在80分及以上的学生成绩的平均数为87.50 -
5、已知圆台下底面的正底面在半径为2的球面上,圆台的下底面过球心,上底面半径为1,则圆台的体积为( )A、 B、 C、 D、
-
6、已知是等差数列的前 n 项和,且 , , 则( )A、 B、的最小值为 C、数列为递减数列 D、
-
7、从集合中依次不放回的任取两个数,记事件 “第一次取出的数字是1”,事件”取出的两个数之和为7”,下列说法不正确的是( )A、 B、为不可能事件 C、事件 A,B 相互独立 D、
-
8、已知点 , , 为坐标原点,向量 , 则=( )A、 B、 C、 D、
-
9、若 , 且 , 则( )A、 B、 C、 D、
-
10、集合. 则( )A、 B、 C、 D、
-
11、已知数列的各项均为正数,其前n项的积为 , 记 , .
(1)若数列为等比数列,数列为等差数列,求数列的公比.
(2)若 , , 且
①求数列的通项公式.
②记 , 那么数列中是否存在两项 , (s,t均为正偶数,且),使得数列 , , , 成等差数列?若存在,求s,t的值;若不存在,请说明理由.
-
12、已知双曲线:的虚轴长为4,直线为双曲线的一条渐近线.
(1)求双曲线的标准方程;
(2)记双曲线的左、右顶点分别为 , , 斜率为正的直线过点 , 交双曲线于点 , (点在第一象限),直线交轴于点 , 直线交轴于点 , 记面积为 , 面积为 , 求证:为定值.
-
13、如图,已知四边形与均为直角梯形,平面平面EFAD, , , 为的中点,.
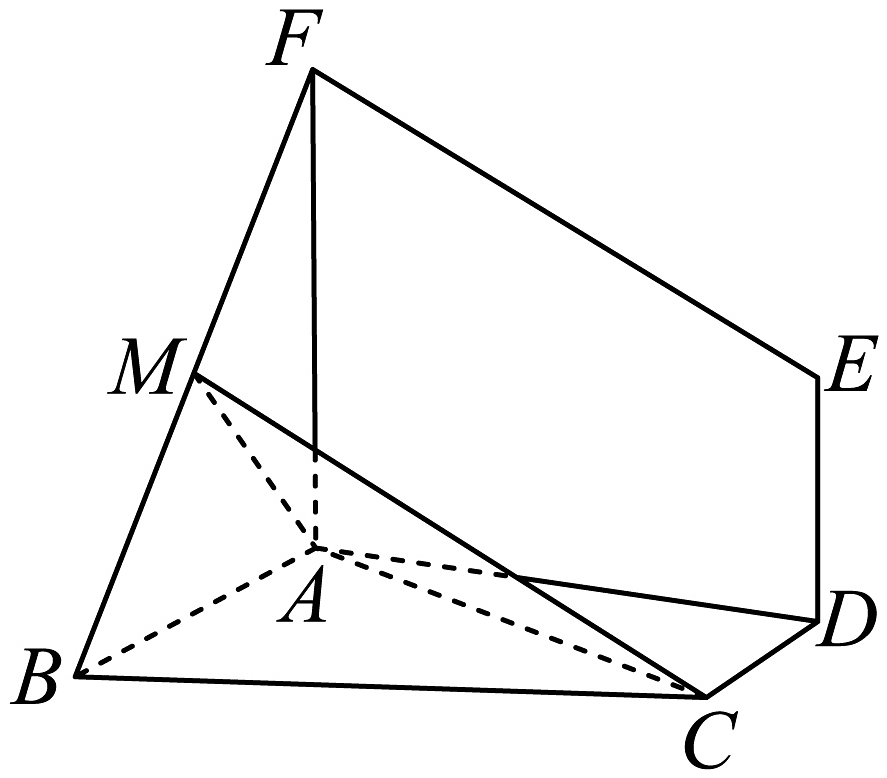 (1)、证明: , , , 四点共面;(2)、求平面与平面夹角的余弦值.
(1)、证明: , , , 四点共面;(2)、求平面与平面夹角的余弦值. -
14、设函数.(1)、当时,求曲线在处的切线方程;(2)、若为增函数,求的取值范围.
-
15、在平面直角坐标系xOy中,已知点 , , 是直线上任意一点,则 .
-
16、如图,四棱台的底面是正方形, , 底面.动点满足 , 则下列判断正确的是( )
 A、点可能在直线上 B、点可能在直线上 C、若点在底面内,则三棱锥的体积为定值 D、若点在棱上,则
A、点可能在直线上 B、点可能在直线上 C、若点在底面内,则三棱锥的体积为定值 D、若点在棱上,则 -
17、已知函数在时满足恒成立,且在区间内,仅存在三个数 , , , 使得 , 则( )A、 B、 C、 D、
-
18、设、分别是椭圆的左、右焦点,过的直线交椭圆于、两点,在轴上的截距为 , 若 , 且轴,则此椭圆的长轴长为( )A、 B、 C、 D、
-
19、在ABC中, , , , 与BE的交点为 , 若 , 则的长为( )A、 B、 C、2 D、
-
20、已知数列为等差数列,则“”是“”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件