-
1、已知集合 , 集合 , 则( )A、 B、 C、 D、
-
2、我们约定:若两个函数的极值点个数相同,并且图象从左到右看,极大值点和极小值点分布的顺序相同,则称这两个函数的图象“相似”.已知 , 则下列给出的函数其图象与的图象“相似”的是( )A、 B、 C、 D、
-
3、已知函数是其导函数.若存在且 , 满足 , 则( )A、 B、 C、 D、
-
4、已知函数(e为自然对数的底数,)(1)、讨论的单调性;(2)、证明:当时, .
-
5、已知函数在处取得极值1.
(1)求 , 的值;
(2)求在上的最大值和最小值.
-
6、混放在一起的6件不同的产品中,有2件次品,4件正品.现需通过检测将其区分,每次随机抽取一件进行检测,检测后不放回,直到检测出2件次品或者检测出4件正品时检测结束.(1)、一共抽取了4次检测结束,有多少种不同的抽法?(2)、若第一次抽到的是次品且第三次抽到的是正品,检测结束时有多少种不同的抽法?
(要求:解答过程要有必要的文字说明和步骤,结果以数字呈现)
-
7、已知函数的定义域为 , 为的导函数,且满足 , 则不等式的解集是.
-
8、已知曲线 , 过点作该曲线的两条切线,切点分别为 , , 则.
-
9、已知数列的首项为4,且满足 , 则( )A、为等差数列 B、为递增数列 C、的前项和 D、的前项和
-
10、用半径为1的圆形铁皮剪出一个扇形制成一个圆锥形容器,容器高为 , 当容器的容积最大时,( )A、 B、 C、 D、
-
11、已知函数与的图象如图所示,则函数
 A、在区间上是减函数 B、在区间上是减函数 C、在区间上减函数 D、在区间上是减函数
A、在区间上是减函数 B、在区间上是减函数 C、在区间上减函数 D、在区间上是减函数 -
12、等比数列的前n项和为 , 若 , , 则( )A、24 B、12 C、24或-12 D、-24或12
-
13、若 , 则( )A、0 B、2 C、-2 D、-4
-
14、若 , 则( )A、30 B、20 C、12 D、6
-
15、已知抛物线的焦点为F,在第一象限内的点和第二象限内的点都在抛物线C上,且直线过焦点F.按照如下方式依次构造点:过点作抛物线C的切线与x轴交于点 , 过点作x轴的垂线与抛物线C相交于点 , 设点的坐标为 . 用同样的方式构造点 , 设点的坐标为 .(1)、证明:数列都是等比数列;(2)、记 , 求数列的前n项和;(3)、证明:当时,直线都过定点.
-
16、在平行四边形中(如图1), , 为的中点,将等边沿折起,连接 , 且(如图2).
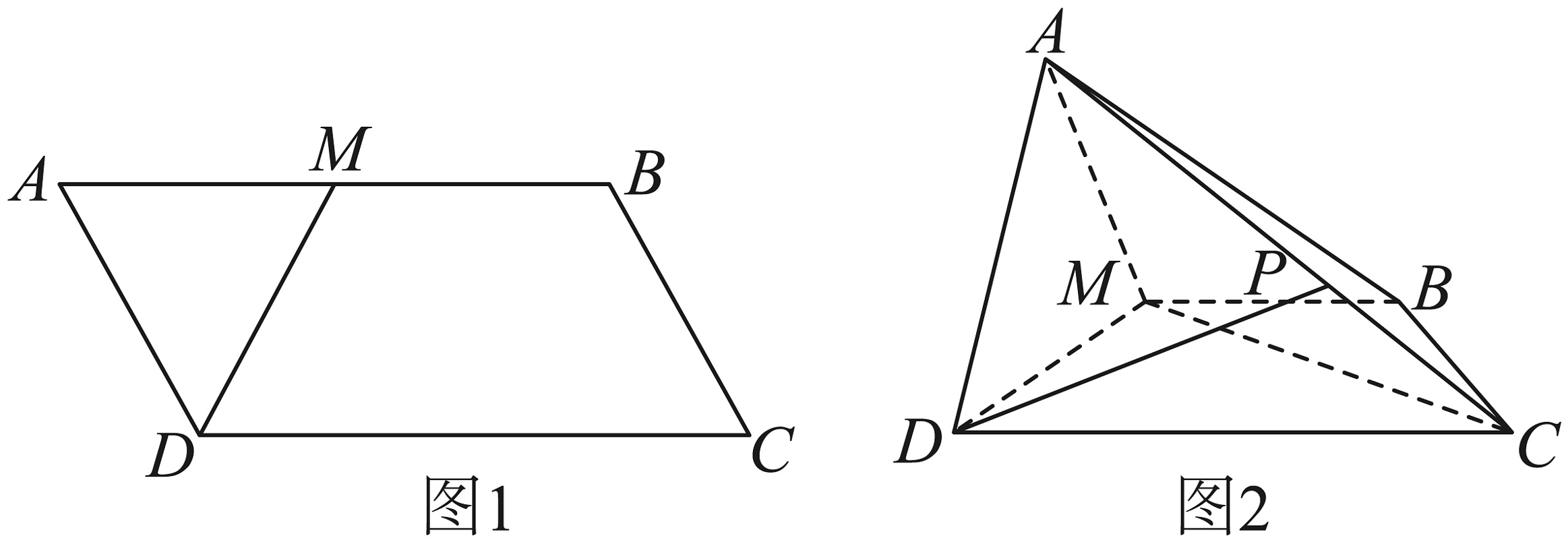 (1)、求证:平面;(2)、求直线与平面所成角的正弦值;(3)、点在线段上,且满足 , 求平面与平面所成角的余弦值.
(1)、求证:平面;(2)、求直线与平面所成角的正弦值;(3)、点在线段上,且满足 , 求平面与平面所成角的余弦值. -
17、现市场上治疗某种疾病的药品有两种,其治愈率与患者占比如表所示,为试验一种新药 , 在有关部门批准后,某医院把此药给100个病人服用.设药的治愈率为 , 且每位病人是否被治愈相互独立.
A
B
C(新药)
治愈率
患者占比
(1)、记100个病人中恰有80人被治愈的概率为 , 求的最大值点;(2)、设用新药的患者占比为(药品减少的患者占比,均为新药增加占比的一半, , 以(1)问中确定的作为的值,从已经用药的患者中随机抽取一名患者,求该患者痊愈的概率(结果用表示)(3)、按照市场预测,使用新药的患者占比能达到以上,不足的概率为 , 不低于且不超过的概率为 , 超过的概率为 , 某药企计划引入药品的生产线,但生产线运行的条数受患者占比的影响,关系如下表:患者占比
最多投入生产线条数
1
2
3
若某条生产线运行,年利润为1000万,若某条生产线未运行,年亏损300万,欲使该药企生产药品的年总利润均值最大,应引入几条生产线?
-
18、记的内角 , , 的对边分别 , , , 已知 .(1)、求;(2)、设是边中点,若 , 求 .
-
19、已知四棱柱中,底面是平行四边形, , 底面 , , 点是四棱柱表面上的一个动点,且直线与所成的角为 , 则点的轨迹长度为 .
-
20、已知集合 , 则 .