-
1、第十九届亚运会将于2023年9月23日至10月8在中国杭州举办,为了了解我市居民对杭州亚运会相关信息和知识的掌握情况,某学校组织学生开展社会实践活动,采用问卷的形式随机对我市100名居民进行了调查.为了方便统计分析,调查问卷满分20分,得分情况制成如下频率分布直方图.
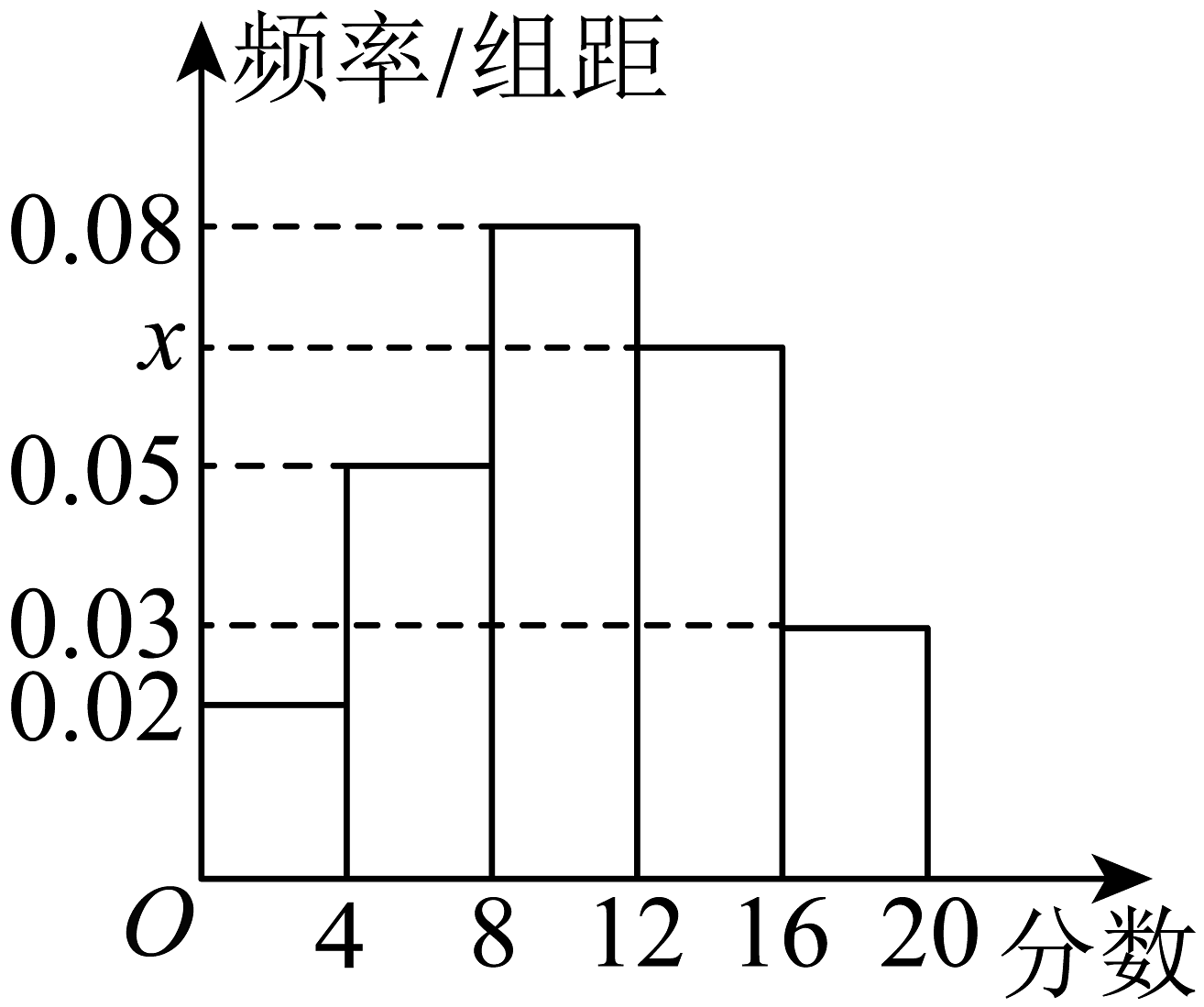 (1)、求的值;(2)、根据频率分布直方图,估计这100名居民调查问卷中得分的
(1)、求的值;(2)、根据频率分布直方图,估计这100名居民调查问卷中得分的(i)第70百分位数(结果用分数表示);
(ii)平均值(各组区间的数据以该组区间的中间值作代表).
-
2、如图,在正三棱柱中,已知 , , 是棱的中点.
 (1)、求证:平面;(2)、该正三棱柱被平面截去一个棱锥 , 求剩余部分的体积.
(1)、求证:平面;(2)、该正三棱柱被平面截去一个棱锥 , 求剩余部分的体积. -
3、已知向量、满足: ,(1)、求;(2)、求与夹角的余弦值;(3)、若向量与共线,求实数的值.
-
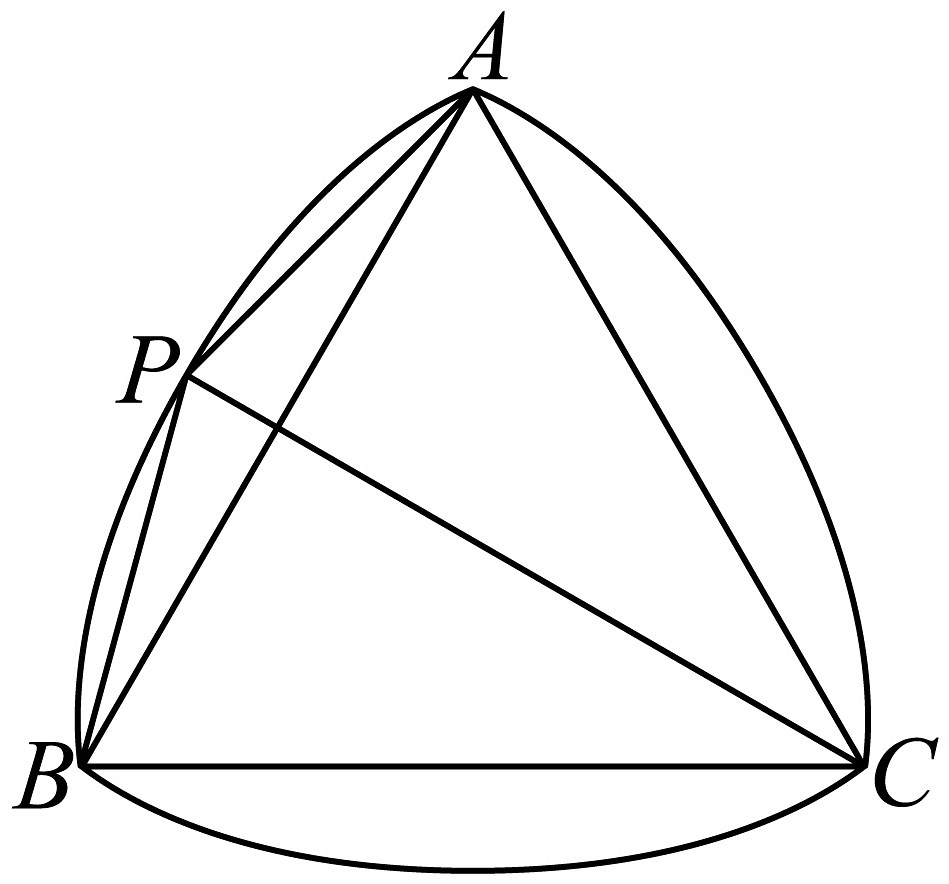
4、德国机械学家莱洛设计的莱洛三角形在工业领域应用广泛.如图,分别以等边三角形的顶点为圆心,以边长为半径作圆弧,由这三段圆弧组成的曲边三角形即为莱洛三角形.若该等边三角形的边长为4,为弧上的一个动点,则的最小值为.
-
5、若圆锥的母线长为 , 轴截面是等腰直角三角形,则该圆锥的体积是 .
-
6、已知复数(为虚数单位),则 .
-
7、如图,棱长为2的正方体中中,下列结论正确的是( )
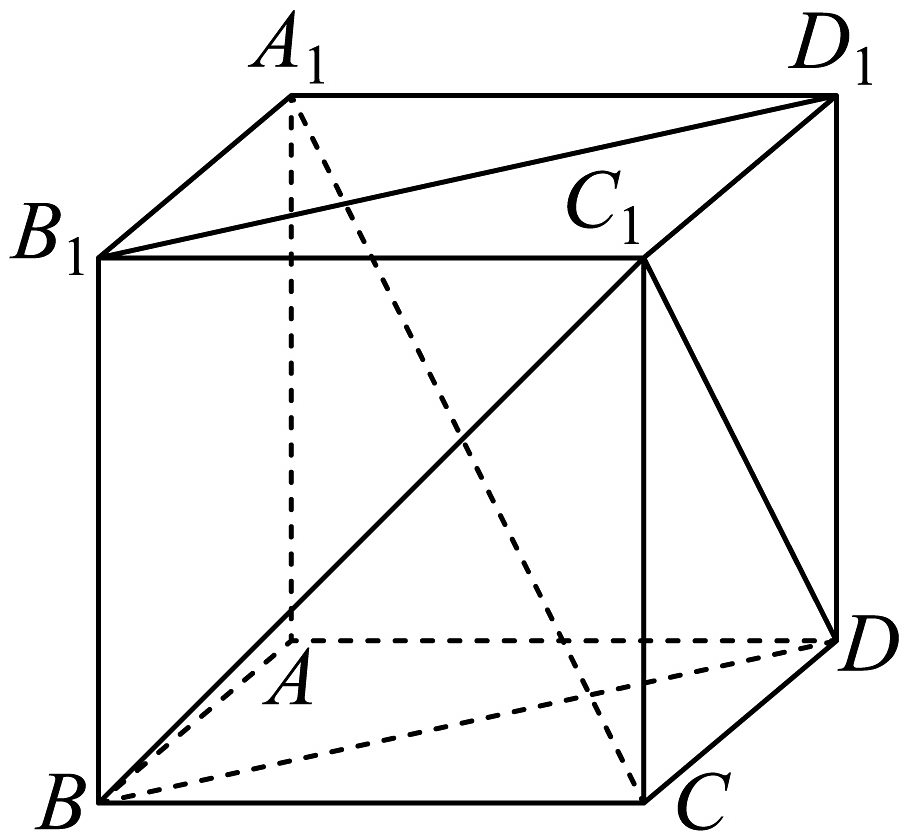 A、异面直线与所成的角为 B、直线与平面所成的角为 C、二面角平面角的正切值为 D、点到平面的距离为
A、异面直线与所成的角为 B、直线与平面所成的角为 C、二面角平面角的正切值为 D、点到平面的距离为 -
8、如图,是正六边形的中心,则( )
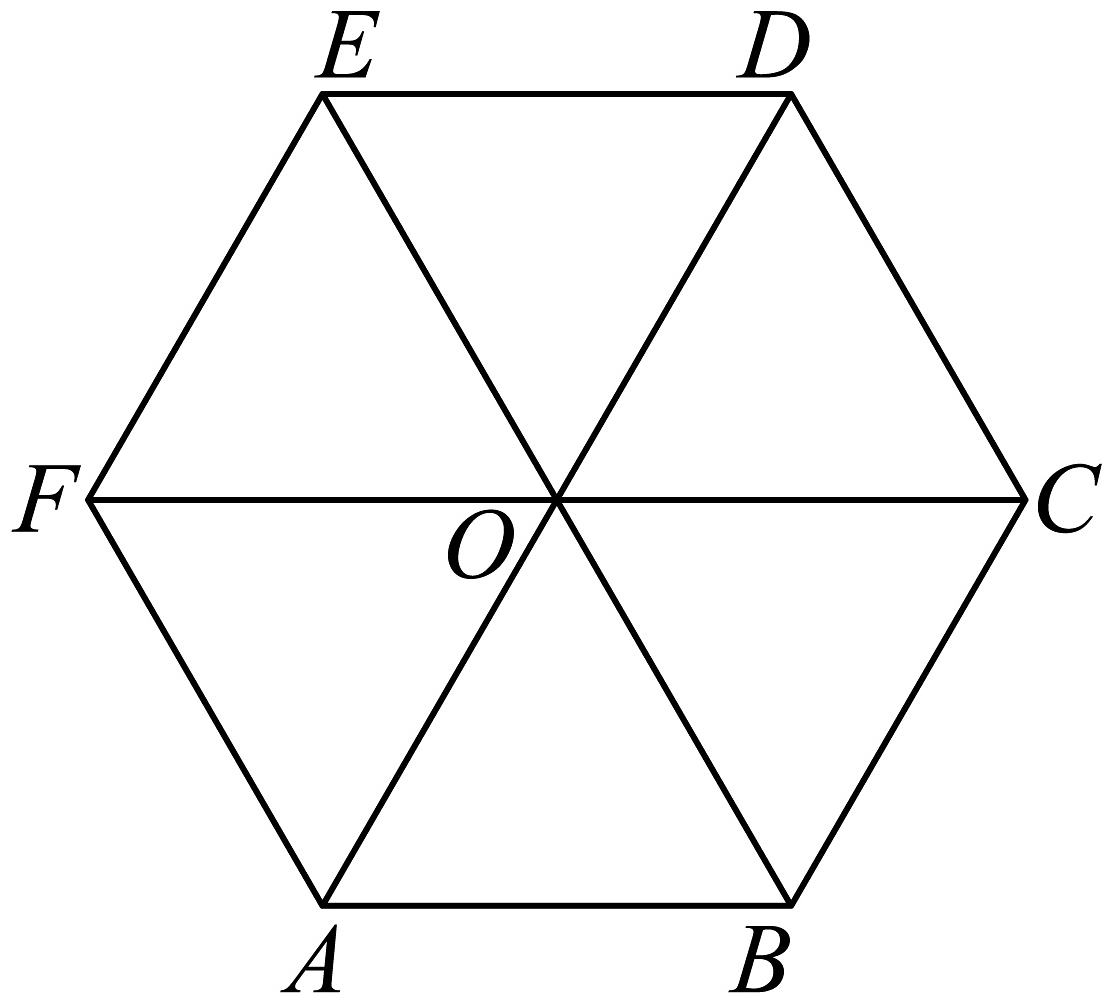 A、 B、 C、 D、在上的投影向量为
A、 B、 C、 D、在上的投影向量为 -
9、某新能源汽车4S店2024年6月到2025年3月连续10个月的销量依次为(单位:辆):16,19,24,25,25,27,32,37,35,40,则关于这组数据的结论正确的是( )A、极差为24 B、平均数为28 C、众数为25 D、中位数为25
-
10、已知圆台上下底面圆的半径分别为1,3,高为4,则该圆台的侧面积为( )A、 B、 C、 D、
-
11、若 , , 与的夹角为 , 则( )A、 B、 C、2 D、28
-
12、已知的方差为3,则的方差为( )A、6 B、7 C、12 D、18
-
13、已知 , 是两条不同的直线, , , 是三个不同的平面,则下列命题中正确的是( )A、若 , , 则 B、若 , , 则 C、若 , , 则 D、若 , , 则
-
14、现有一组数据12,13,15,14,12,20,18,19,则这组数据的第55百分位数为( )A、14 B、14.5 C、15 D、18
-
15、1班有学生45人,2班有学生27人,3班有学生36人,用分层抽样的方法从这三个班中抽出24人参加数学趣味活动,那么1班被抽取的人数是( )A、9 B、10 C、11 D、以上都不正确
-
16、已知是定义在上的单调递减函数,且对 , 均有 , 若不等式在恒成立,则实数的最大值是.
-
17、已知定义在R上的二次函数 , 且在上的最小值是7.(1)、求实数的值;(2)、设函数 , 方程在上是否存在两个不等实根?若存在,请说明与的大小关系,若不存在,请说明理由.
-
18、如图,在四棱锥中,底面为正方形,底面 , 为线段的中点,为线段上的动点.
 (1)、求四棱锥的体积;(2)、求证:平面平面;(3)、若点为中点,求二面角的平面角的余弦值.
(1)、求四棱锥的体积;(2)、求证:平面平面;(3)、若点为中点,求二面角的平面角的余弦值. -
19、已知函数 .(1)、求的值;(2)、把函数化成的形式,并求的最小正周期;(3)、求出满足方程的所有的取值集合.
-
20、已知为正实数,且 , 则的最小值为 .