-
1、某新能源汽车4S店2024年6月到2025年3月连续10个月的销量依次为(单位:辆):16,19,24,25,25,27,32,37,35,40,则关于这组数据的结论正确的是( )A、极差为24 B、平均数为28 C、众数为25 D、中位数为25
-
2、已知圆台上下底面圆的半径分别为1,3,高为4,则该圆台的侧面积为( )A、 B、 C、 D、
-
3、若 , , 与的夹角为 , 则( )A、 B、 C、2 D、28
-
4、已知的方差为3,则的方差为( )A、6 B、7 C、12 D、18
-
5、已知 , 是两条不同的直线, , , 是三个不同的平面,则下列命题中正确的是( )A、若 , , 则 B、若 , , 则 C、若 , , 则 D、若 , , 则
-
6、现有一组数据12,13,15,14,12,20,18,19,则这组数据的第55百分位数为( )A、14 B、14.5 C、15 D、18
-
7、1班有学生45人,2班有学生27人,3班有学生36人,用分层抽样的方法从这三个班中抽出24人参加数学趣味活动,那么1班被抽取的人数是( )A、9 B、10 C、11 D、以上都不正确
-
8、已知是定义在上的单调递减函数,且对 , 均有 , 若不等式在恒成立,则实数的最大值是.
-
9、已知定义在R上的二次函数 , 且在上的最小值是7.(1)、求实数的值;(2)、设函数 , 方程在上是否存在两个不等实根?若存在,请说明与的大小关系,若不存在,请说明理由.
-
10、如图,在四棱锥中,底面为正方形,底面 , 为线段的中点,为线段上的动点.
 (1)、求四棱锥的体积;(2)、求证:平面平面;(3)、若点为中点,求二面角的平面角的余弦值.
(1)、求四棱锥的体积;(2)、求证:平面平面;(3)、若点为中点,求二面角的平面角的余弦值. -
11、已知函数 .(1)、求的值;(2)、把函数化成的形式,并求的最小正周期;(3)、求出满足方程的所有的取值集合.
-
12、已知为正实数,且 , 则的最小值为 .
-
13、如图,是根据某家长某月的通话明细清单,按每次通话时间长短画出的频率分布直方图,估计这组数据的第50百分位数为.(保留小数点后面一位)
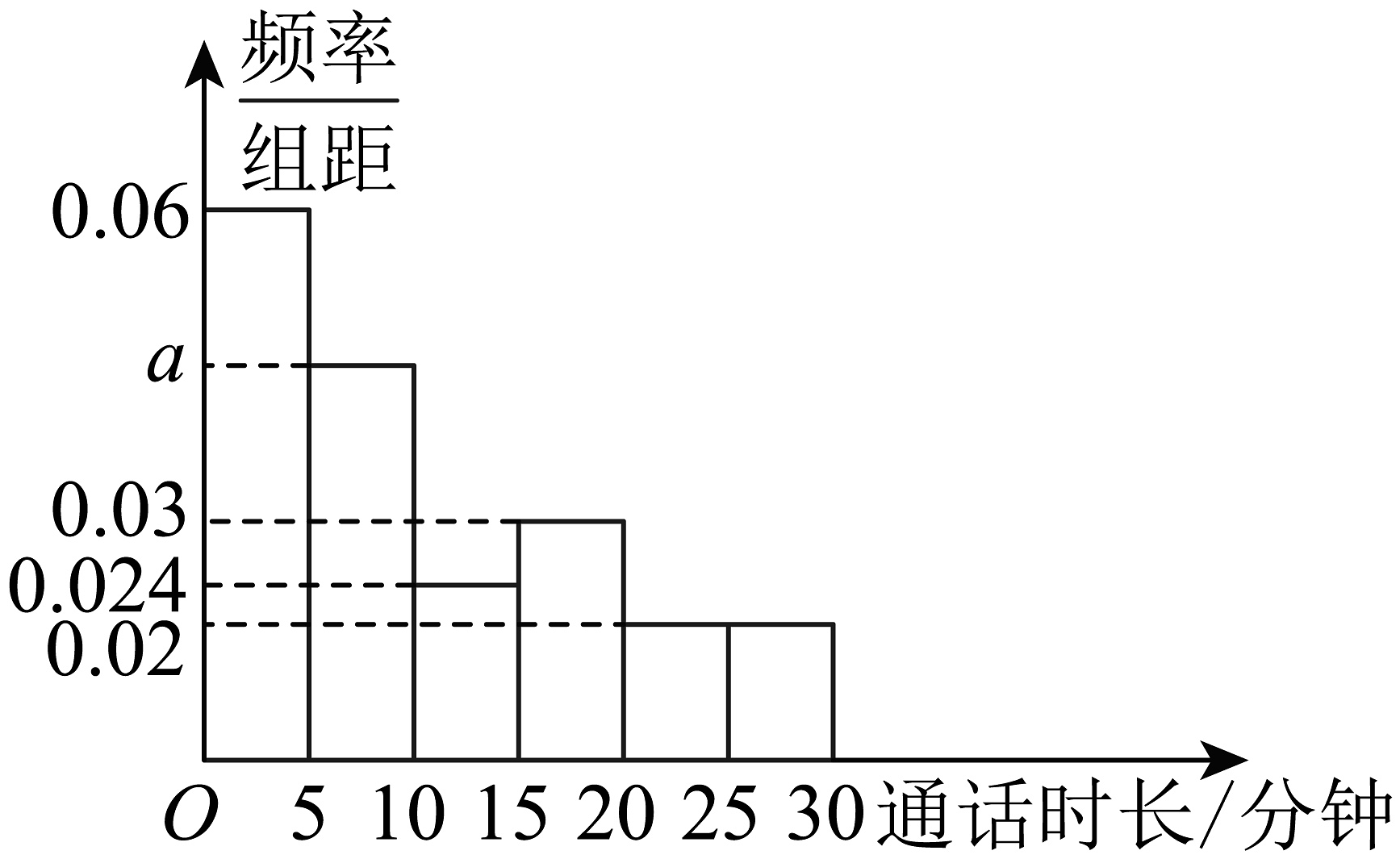
-
14、袋中装有3个除颜色外完全相同的球,其中2个白球,1个黑球,从中任取两个球,则取出的球颜色不相同的概率是 .
-
15、如图,在棱长为2的正方体中,为棱中点,为棱上的动点(不包括端点),则( )
 A、直线与直线相交 B、存在点 , 使得 C、当取最小值时,点为中点 D、过三点的截面为五边形
A、直线与直线相交 B、存在点 , 使得 C、当取最小值时,点为中点 D、过三点的截面为五边形 -
16、已知函数是定义域为的奇函数,当时, , 则下列选项正确的是( )A、图象过定点 B、值域为 C、在定义域上单调 D、函数一定存在单调增区间
-
17、下列各式一定成立的是( )A、 B、 C、 D、
-
18、定义分段函数 , 其中、为实数.已知函数在区间内恰好有个零点,则满足条件的组合可能是( )A、 B、 C、 D、
-
19、已知正边形的边长为 , 内切圆的半径为 , 外接圆的半径为 , 则的值为( )A、 B、 C、 D、
-
20、某商品当前价格为100元/件,预计下个月价格上涨或下跌(两种情况概率各).若需在当前和下个月各购买1件(共2件),有两种策略:
策略P:按需购买,当前买1件(100元),下个月按当时价格买1件;
策略Q:当前一次性购买2件,享受总价95折(即两件总价为元).
不考虑资金时间价值,预计哪种策略的平均总成本更低?( )
A、策略P B、策略Q C、平均总成本相同 D、需根据价格波动幅度判断