-
1、若 , , 且 , 则实数的值是
-
2、已知正方体的棱长为 , 点为中点,动点在正方形内(包括边界),则下列说法正确的是( )A、若 , 则的长度是 B、若平面 , 则的最小值是 C、若 , 则点的轨迹长度是 D、若平面 , 则点的位置唯一
-
3、已知等比数列的公比为q,前n项和 , 设 , 记的前n项和为 , 则下列判断正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则
-
4、已知圆 , , 则下列说法正确的是( )A、当时,圆与圆相离 B、当时,是圆与圆的一条公切线 C、当时,圆与圆相交 D、当时,圆与圆的公共弦所在直线方程是
-
5、已知双曲线的右焦点为 , 过的直线(为常数)与在第一象限交于点.若(为原点),则的离心率是( )A、 B、 C、 D、5
-
6、已知 , 若 , 则( )A、 B、 C、 D、
-
7、如图,八面体的每个面都是正三角形,若四边形是边长为4的正方形,则( )
 A、异面直线和所成的角为 B、平面和平面有相同的法向量 C、异面直线和的距离为 D、二面角的余弦值为
A、异面直线和所成的角为 B、平面和平面有相同的法向量 C、异面直线和的距离为 D、二面角的余弦值为 -
8、如图,直三棱柱中, , , , M是的中点,N是BC的中点,过点N作与平面平行的直线PN,交于点P.
 (1)、证明:平面AMN;(2)、求与平面PMN所成角的正弦值;(3)、求点P到平面AMN的距离.
(1)、证明:平面AMN;(2)、求与平面PMN所成角的正弦值;(3)、求点P到平面AMN的距离. -
9、2024年10月30日,我国神舟十九号载人飞船顺利升空,并与中国空间站成功对接.为弘扬航天精神,某大学举办了一次“逐梦星辰大海——航天杯”知识竞赛.竞赛分为初赛和决赛,初赛规则为:每位参赛者依次回答5道题,连续答错2道题或5道题都答完,则比赛结束.假定大学生张某答对这5道题的概率依次为 , 且各题是否答对互不影响.(1)、若至少连续答对4道题,可得到一张直升卡,直接进入决赛,求张某得到直升卡的概率;(2)、记张某初赛结束时已答题的个数为 , 求的分布列及数学期望.
-
10、已知的内角所对的边分别为 , 且 .(1)、求角;(2)、若的面积为 , 为的中点,求长度的最小值.
-
11、为了解某地农村经济情况,对该地农户家庭年收入进行抽样调查,将农户家庭年收入的调查数据整理得到如下频率分布直方图:

根据此频率分布直方图,下面结论中正确的是( )
A、估计该地农户家庭年收入的平均值不超过6.5万元 B、估计该地有一半以上的农户,其家庭年收入介于4.5万元至8.5万元之间 C、若用分层抽样的方法在该地农户家庭年收入在 , , 三组中共抽取48个家庭进行初步访谈,则年收入在的家庭应抽24个 D、从抽样的12组中的每组中抽出一个数据,得到共12个家庭的具体收入数据,若数据a与这12个家庭的收入数据的差的平方和最小,则数据a必为这12个家庭收入数据的平均数 -
12、函数的部分图象大致为( ).A、
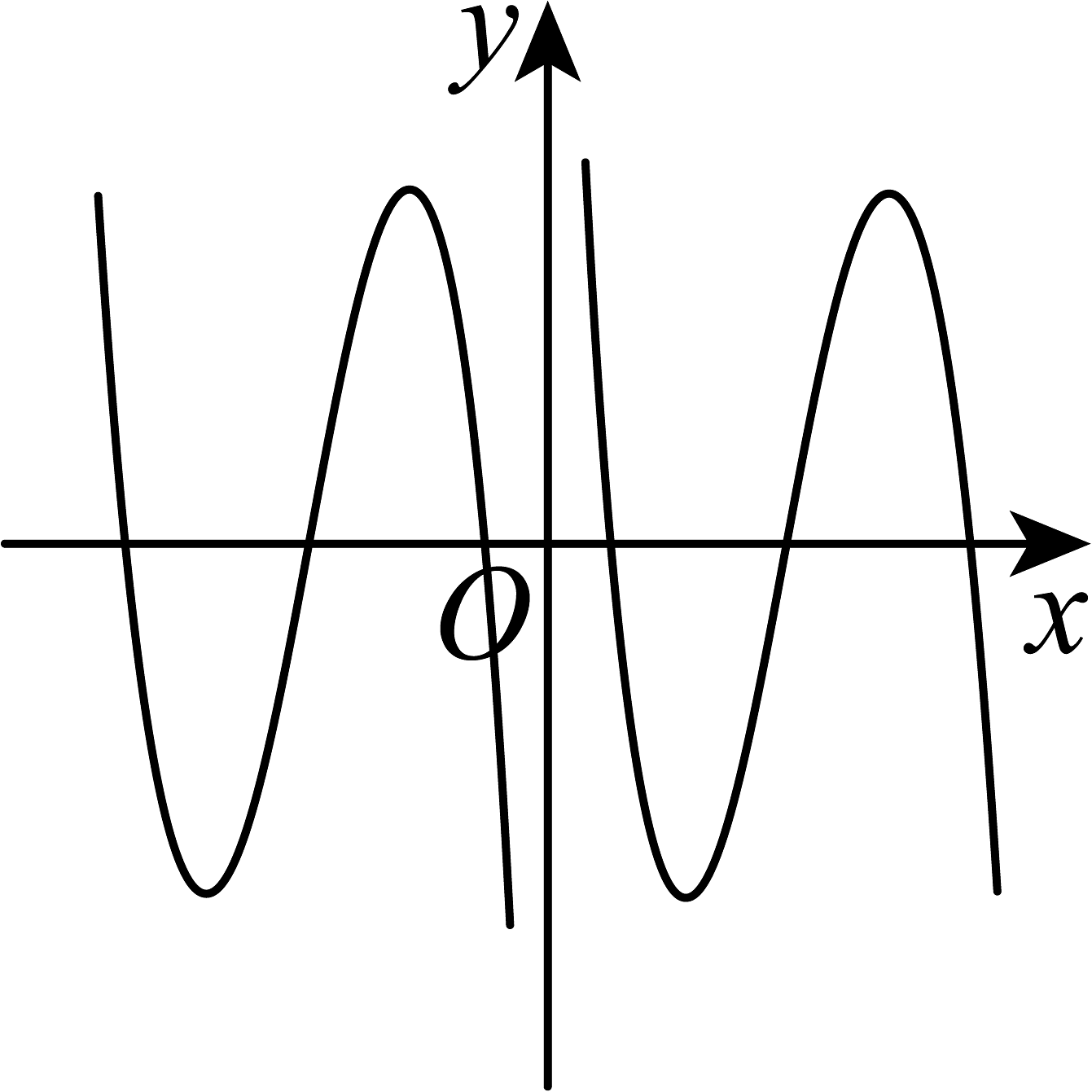 B、
B、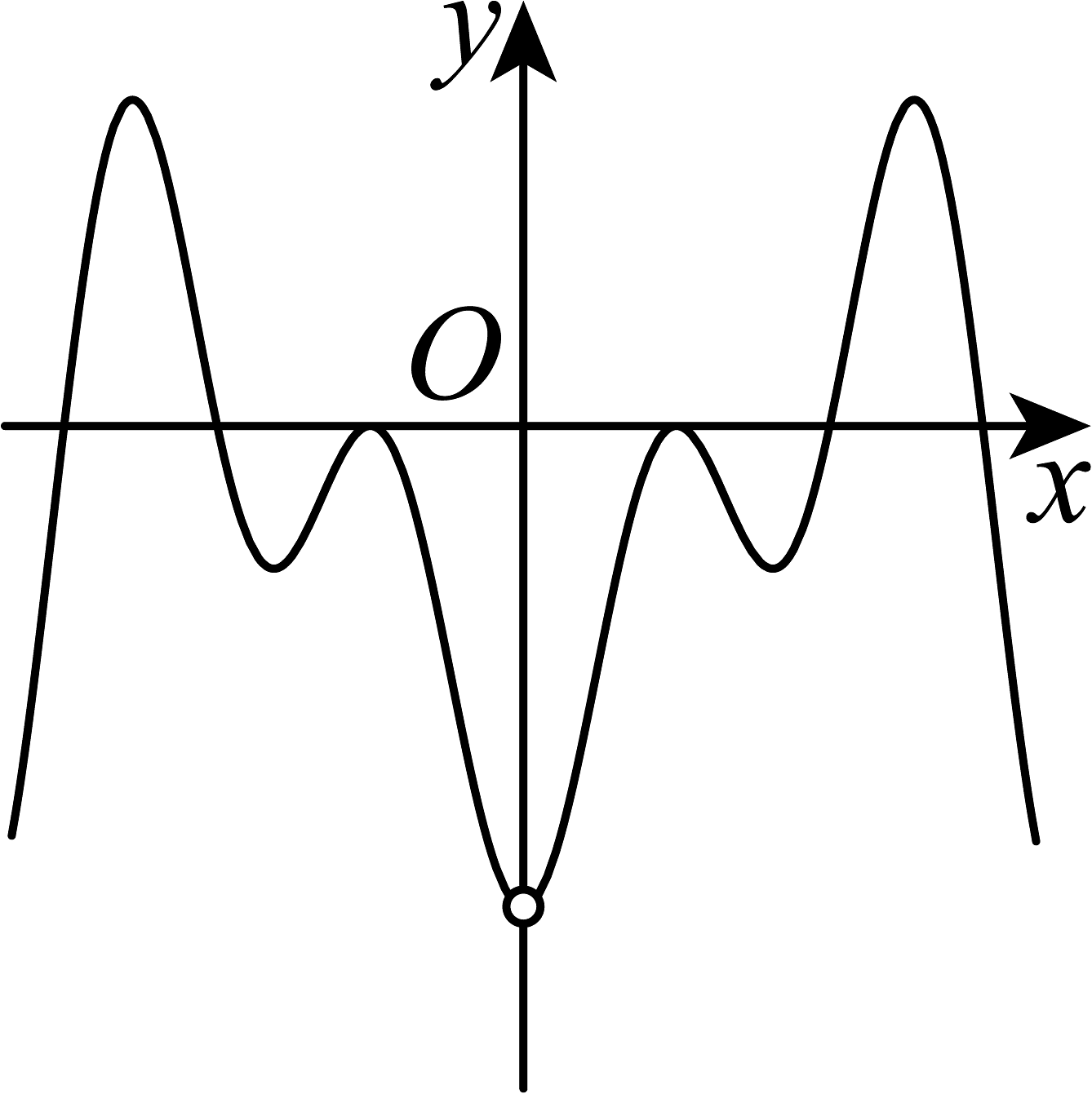 C、
C、 D、
D、
-
13、已知 , 则( )A、 B、 C、 D、
-
14、设集合 , , 则的元素个数为( )A、 B、3 C、2 D、1
-
15、设函数在处有极值,且 , 则称为函数的“F点”.(1)、判断函数是否存在F点;(2)、设函数 , 当存在F点,求k的值;(3)、设函数 , 存在两个不相等的“F点” , , 且 , 求a取值范围.
-
16、已知直三棱柱中,侧面为正方形, , E,F分别为和的中点,D为棱上的点. .
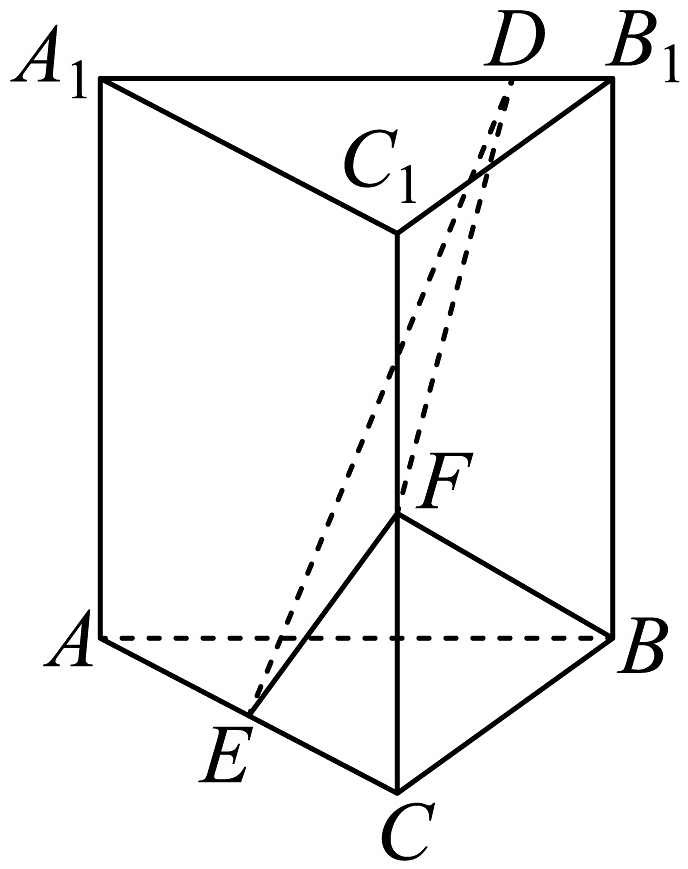 (1)、证明:平面(2)、证明:(3)、当为何值时,面与面DFE所成的二面角的正弦值最小,并求此最小值.
(1)、证明:平面(2)、证明:(3)、当为何值时,面与面DFE所成的二面角的正弦值最小,并求此最小值. -
17、某企业创新形式推进党史学习教育走深走实,举行两轮制的党史知识竞赛初赛,每部门派出两个小组参赛,两轮都通过的小组才具备参与决赛的资格,该企业某部门派出甲、乙两个小组,若第一轮比赛时两组通过的概率分别是 , , 第二轮比赛时两组通过的概率分别是 , , 两轮比赛过程相互独立.
(1)若将该部门获得决赛资格的小组数记为 , 求的分布列与数学期望;
(2)比赛规定:参与决赛的小组由4人组成,每人必须答题且只答题一次(与答题顺序无关),若4人全部答对就给予奖金,若没有全部答对但至少2人答对就被评为“优秀小组".该部门对通过初赛的某一小组进行党史知识培训,使得每个成员答对每题的概率均为()且相互独立,设该参赛小组被评为“优秀小组”的概率为 , 当时,最大,试求的值.
-
18、某校高二年级为研究学生数学成绩与语文成绩的关系,采取有放回的简单随机抽样,从高二学生中抽取样本容量为200的样本,将所得数学成绩与语文成绩的样本观测数据整理如下:
语文成绩
合计
优秀
不优秀
数学成绩
优秀
50
30
80
不优秀
40
80
120
合计
90
110
200
(1)、根据的独立性检验,能否认为数学成绩与语文成绩有关联?(2)、现从该校学生中任选一人,A表示“选到的学生语文成绩不优秀”,B表示“选到的学生数学成绩不优秀”.请利用样本数据,估计的值.附: .
0.05
0.01
0.001
3.841
6.635
10.828
-
19、已知函数在点处的切线方程为 .(1)、求实数a,b的值:(2)、求函数在上的最大值.
-
20、设集合A中的元素皆为无重复数字的三位正整数,且集合A中的元素任意两个之积皆为偶数,则集合A中元素为偶数的个数最大值为 , 集合A中元素个数的最大值为 .