-
1、已知数列满足 , 且是关于的方程的两个根.(1)、求;(2)、设 , 求数列的前21项和 .
-
2、有个大小外观一致、重量各不相同的小纸箱和一个天平,设为确保找到第二重的小纸箱时使用天平的最少次数.则; .
-
3、圆锥曲线在物理光学上都有各自光学性质.在双曲线中,从一个焦点发出的光线,经双曲线反射后,反射光线会散开,但反射光线的反向延长线经过双曲线的另一个焦点.已知双曲线的方程为 , 一束光线从的右焦点射出.经过反射后到达点 . 则光线从到所经过的路径长为 .
-
4、已知函数 , 则 .
-
5、已知函数及其导函数的定义域为 , 若为奇函数, , 且对任意 , , 则下列结论正确的是( )A、 B、 C、 D、
-
6、如图,已知棱长为2的正方体中心为 , 将四棱锥绕直线顺时针旋转之后,得到新的四棱锥 , 则( )
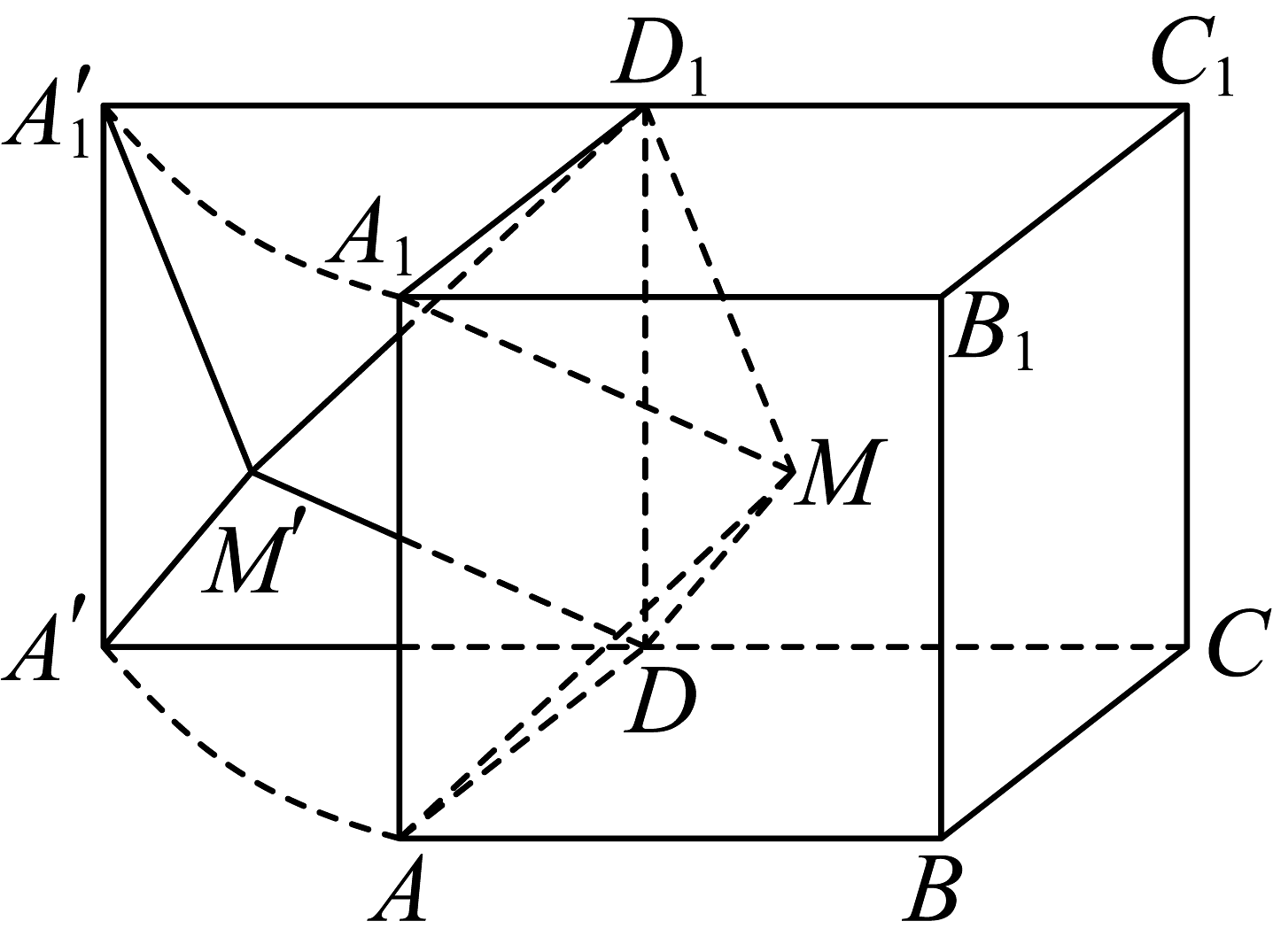 A、 B、当时,四棱锥顶点运动的轨迹长度为 C、当时,平面平面 D、存在旋转的角度 , 使得四点共面
A、 B、当时,四棱锥顶点运动的轨迹长度为 C、当时,平面平面 D、存在旋转的角度 , 使得四点共面 -
7、生活经验告诉我们,儿子的身高与父亲的身高不仅线性相关,而且还是正相关.有人调查了10名男大学生的身高(单位:)及其父亲身高(单位:)的数据 , 已知其中一组数据为 , 且 , 求得经验回归方程为 , 并绘制了如下残差图(残差观测值预测值),则
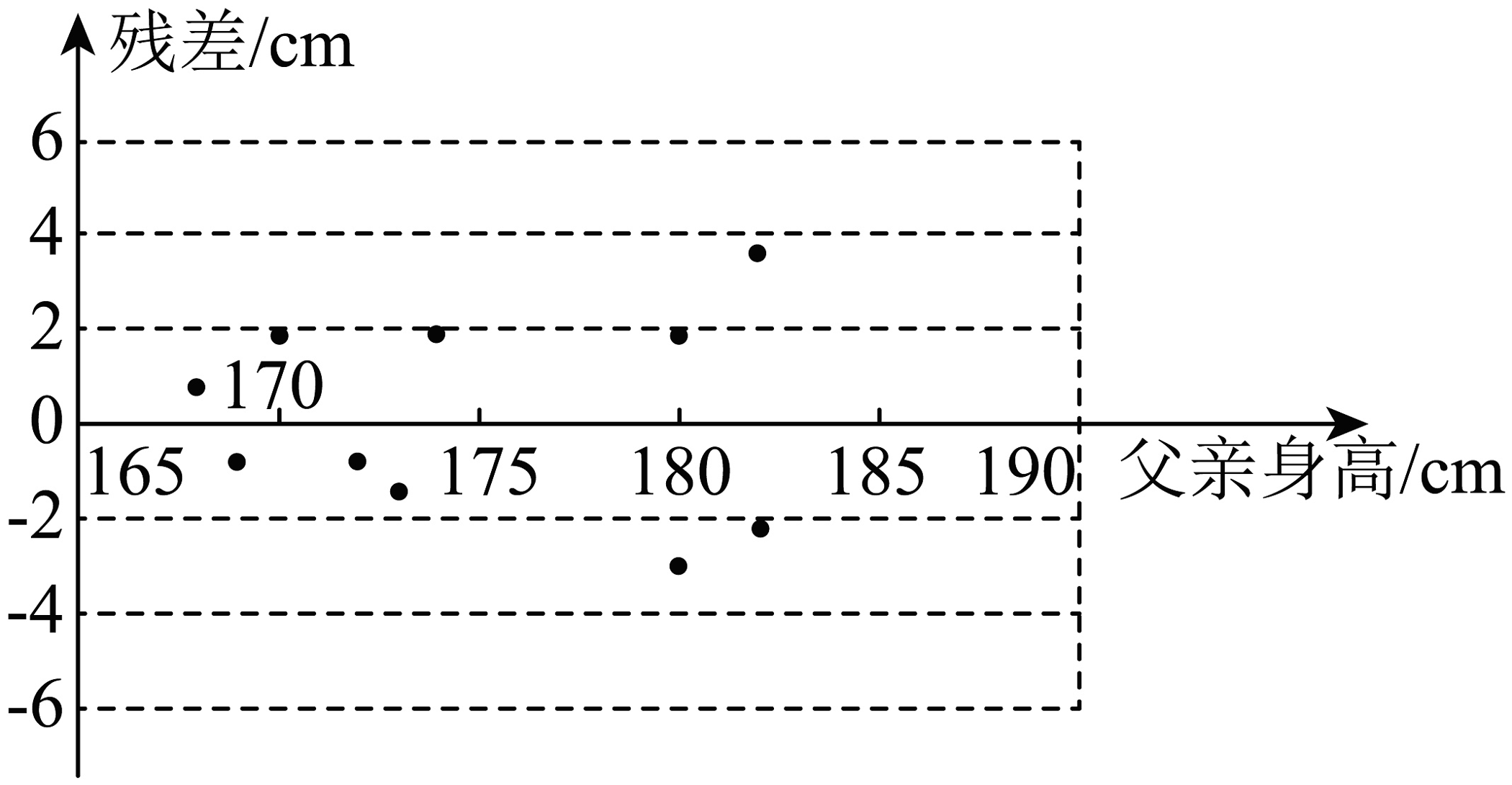 A、这10名男大学生的身高的平均值为176.75 B、由残差图可判定儿子身高与父亲身高的关系不符合上述回归模型 C、数据对应的残差为3.7 D、去掉数据后,重新求得的回归直线的决定系数变小
A、这10名男大学生的身高的平均值为176.75 B、由残差图可判定儿子身高与父亲身高的关系不符合上述回归模型 C、数据对应的残差为3.7 D、去掉数据后,重新求得的回归直线的决定系数变小 -
8、已知函数 , 若存在最小值,则实数的取值范围是( )A、 B、 C、 D、
-
9、在中,角的对边分别为 . 已知 , 且的内角平分线 , 则面积的最小值为( )A、2 B、 C、3 D、
-
10、如图,已知矩形的边长满足 , 以为圆心的圆与相切于 , 则( )
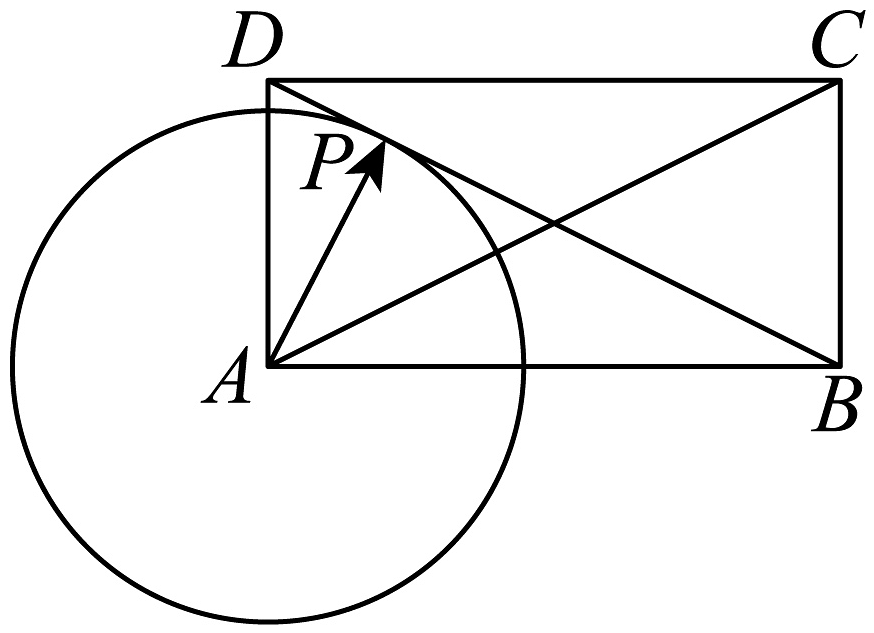 A、 B、 C、8 D、
A、 B、 C、8 D、 -
11、若的展开式中的常数项为31,则( )A、 B、0 C、1 D、2
-
12、将函数的图象向右平移个单位长度,得到函数的图象,则下列结论正确的是( )A、是奇函数 B、的图象关于直线对称 C、在上的值域为 D、在上单调递增
-
13、已知抛物线上的点的横坐标为4,抛物线的焦点为 . 若 , 则的值为( )A、18 B、9 C、4 D、2
-
14、设集合 , 则的元素个数为( )A、6 B、5 C、4 D、3
-
15、复平面上两点对应的复数分别是 , 向量对应的复数为 , 则( )A、17 B、 C、13 D、
-
16、已知数表 , 其中表示数表中第行第列的实数,互不相同,且满足下列条件:①;②.(1)、对于数表 , 若 , 写出所有满足条件的数表;(2)、对于数表 , 当取最小值时,求证:存在正整数 , 使得;(3)、对于数表 , 当n为偶数时,求的最大值.
-
17、已知椭圆的焦距为 , 其短轴的两个端点与长轴的一个端点构成正三角形.(1)、求椭圆的标准方程;(2)、设为的左焦点,为直线上任意一点,过作的垂线交于点 , .
(i)证明:平分线段(其中为坐标原点);
(ii)设线段的中点为 , 若与面积之积是 , 求点的纵坐标.
-
18、如图,在四棱锥中,平面 , , , .
 (1)、证明:平面平面;(2)、若与平面所成角的正弦值为 , 求二面角的余弦值.
(1)、证明:平面平面;(2)、若与平面所成角的正弦值为 , 求二面角的余弦值. -
19、已知公差不为零的等差数列的前项和为 , 若 , 且 , , 成等比数列.(1)、求数列的通项公式;(2)、若 , 求数列的前项和 .
-
20、如图是一座抛物线型拱桥,当水面在l时,拱顶离水面 , 水面宽 . 当水位下降,水面宽为时,拱顶到水面的距离是 .
