-
1、已知两个不同的平面α,β和两条不同的直线m,n满足 , 则是的( )A、充要条件 B、充分不必要条件 C、必要不充分条件 D、既不充分也不必要条件
-
2、已知的面积为 , , , 的内角平分线交边于点 , 则的值为( )A、 B、 C、 D、
-
3、设 , , , 则( )A、 B、 C、 D、
-
4、已知向量与的夹角为 , , , 若 , 则实数( )A、2 B、1 C、 D、
-
5、若复数满足 , 则( )A、 B、 C、 D、
-
6、已知集合 , , 则( )A、 B、 C、 D、
-
7、生物学上,J型增长是指在理想状态下,物种迅速爆发的一种增长方式,其表达式为 , 其中为初始个体数,为最终个体数.若某种群在该模型下,个体数由100增长至120消耗了10天,则个体数由120增长至160消耗的时间大约为( )(参考数据: , )A、14 B、15 C、16 D、17
-
8、在平面直角坐标系中,将双曲线绕着轴旋转一周构成双曲面 , 其中在旋转过程中的所有实轴落在平面内,设所在的平面为 , 平面满足 , 且与之间的距离为.(1)、若点在上,试用含的方程表示(不用说明理由).(2)、设分别是截得的截面.
(i)设分别为上的弦,求所在直线间的距离的取值范围;
(ii)已知截面的圆周上的点恰好构成正边形的顶点,为上一动点,若对任意恒成立,求的取值范围.
-
9、已知函数.(1)、求的图象在点处的切线方程;(2)、求的零点个数;(3)、证明:.
-
10、在中,角A,B,C的对边分别为a,b,c,且.(1)、求的值;(2)、若 , , , 求AD的长.
-
11、函数的极小值是.
-
12、设集合 , 且 , .定义运算:若满足① , 且当且仅当时, , ② , ③这三个条件,则称为上的范数.下列结论正确的是( )A、若为上的范数,且 , 则 B、若为上的范数,则 C、定义运算 , 则为上的范数 D、定义运算 , 则为上的范数
-
13、如图,在直三棱柱中,为的中点,则( )
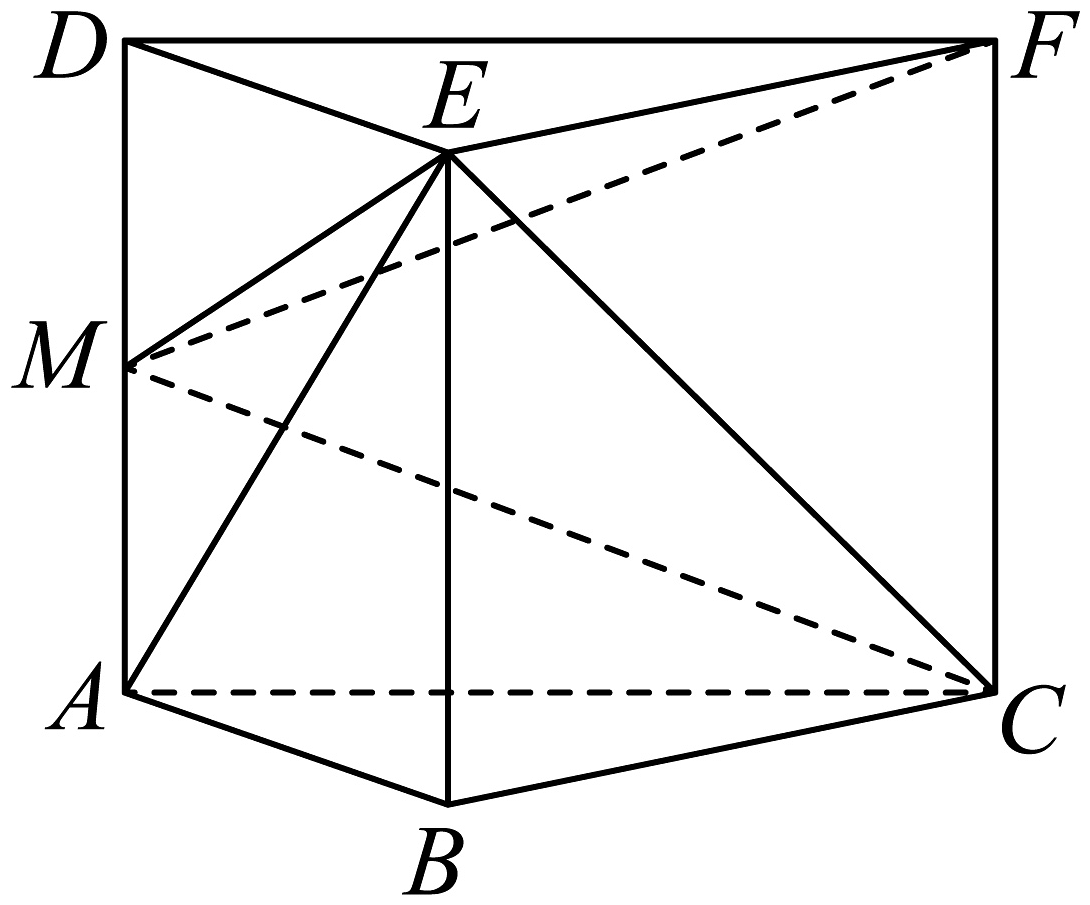 A、 B、三棱锥的体积为 C、直线与所成角的余弦值为 D、三棱锥的外接球的表面积为
A、 B、三棱锥的体积为 C、直线与所成角的余弦值为 D、三棱锥的外接球的表面积为 -
14、已知函数的定义域为 , 对于任意的 , 都有 . 若 , 且在时恒成立,则的取值范围为( )A、 B、 C、 D、
-
15、由阿基米德的著作《关于圆锥体和球体》可知,椭圆的面积等于圆周率与椭圆的长半轴长和短半轴长的乘积.已知椭圆的离心率为分别为的左、右焦点,上一点满足 , 且的面积为 , 则的面积为( )A、 B、 C、 D、
-
16、将函数图象上所有点的横坐标变为原来的 , 纵坐标不变,得到函数的图象,若在上单调,则的取值范围为( )A、 B、 C、 D、
-
17、已知圆上恰有两个点到直线的距离为2,则m的取值范围是( )A、 B、 C、 D、
-
18、已知 , ; , .下列结论正确的是( )A、p是真命题,q是真命题 B、p是真命题,是真命题 C、是真命题,q是真命题 D、是真命题,是真命题
-
19、函数是定义在R上的奇函数,且当时, , 则( )A、 B、 C、4 D、6
-
20、抛物线的焦点为F,是抛物线C上一点,则( )A、10 B、8 C、6 D、4