-
1、已知圆的面积被直线平分,圆 , 则圆与圆的位置关系是( )A、外离 B、相交 C、内切 D、外切
-
2、在三棱柱中,分别是的中点, , 则( )A、 B、 C、 D、
-
3、已知直线与垂直,则( )A、0 B、0或 C、 D、0或
-
4、已知集合 , 则( )A、 B、 C、 D、
-
5、已知函数(为常数,).(1)、讨论函数的奇偶性;(2)、若方程在上有实根,求实数的取值范围.
-
6、已知幂函数 , 且.(1)、求函数的解析式;(2)、若均为正数且 , 求的最小值.
-
7、(1)解不等式
(2)解不等式
-
8、已知关于x的不等式(ax﹣a2﹣4)(x﹣4)>0的解集为A,且A中共含有n个整数,则当n最小时实数a的值为 .
-
9、已知f(x+)=x2+ , 则函数f(x)= .
-
10、若函数(且)经过的定点是P,则P点的坐标是 .
-
11、已知函数的定义域为R, , 则( )A、 B、 C、是奇函数 D、是偶函数
-
12、(多选)以下关于数的大小的结论正确的是( )A、 B、 C、 D、
-
13、下列函数中,既是偶函数又在区间单调递增的是( )A、 B、 C、 D、
-
14、已知不等式的解集为 , 则实数( )A、 B、0 C、1 D、2
-
15、若函数的定义域是 , 则其值域为( ).A、 B、 C、 D、
-
16、已知函数 , 则( )A、 B、 C、0 D、1
-
17、已知椭圆的左、右焦点分别为 , 离心率为 , 经过点且倾斜角为的直线与椭圆交于两点(其中点在轴上方),的周长为8.
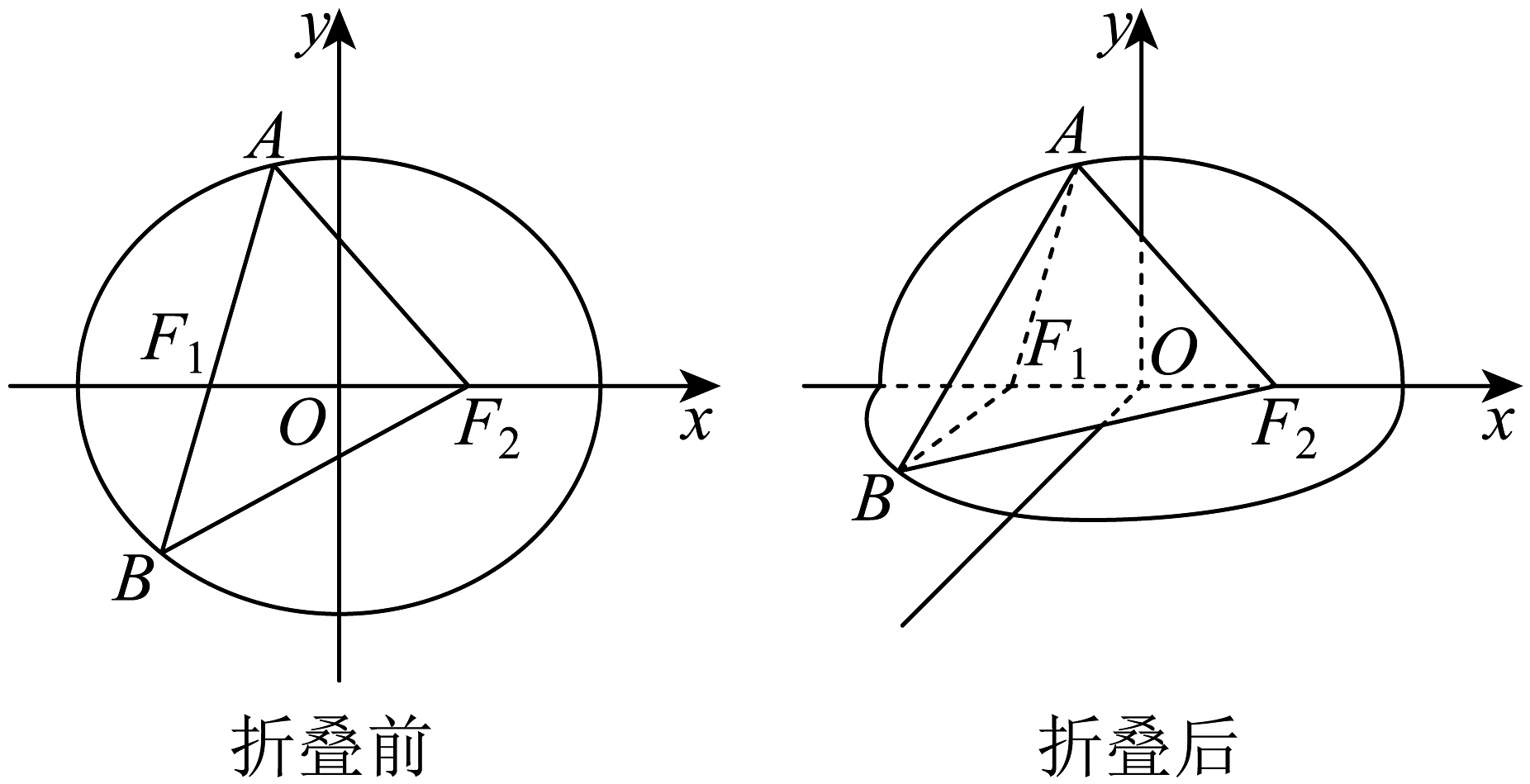 (1)、求椭圆的标准方程;(2)、如图,将平面沿轴折叠,使轴正半轴和轴所确定的半平面(平面)与轴负半轴和轴所确定的半平面(平面)互相垂直.
(1)、求椭圆的标准方程;(2)、如图,将平面沿轴折叠,使轴正半轴和轴所确定的半平面(平面)与轴负半轴和轴所确定的半平面(平面)互相垂直.①若 , 求三棱锥的体积;
②是否存在 , 使得折叠后的周长为与折叠前的周长之比为?若存在,求的值;若不存在,请说明理由.
-
18、如图,已知圆为坐标原点,过点作直线交圆于点 , 过点分别作圆的切线,两条切线相交于点 .
 (1)、若直线的斜率为1,求的值;(2)、求点的轨迹方程;(3)、若两条切线与轴分别交于点 , 求的最小值.
(1)、若直线的斜率为1,求的值;(2)、求点的轨迹方程;(3)、若两条切线与轴分别交于点 , 求的最小值. -
19、如图在四棱锥中, , , , , , 是的中点.
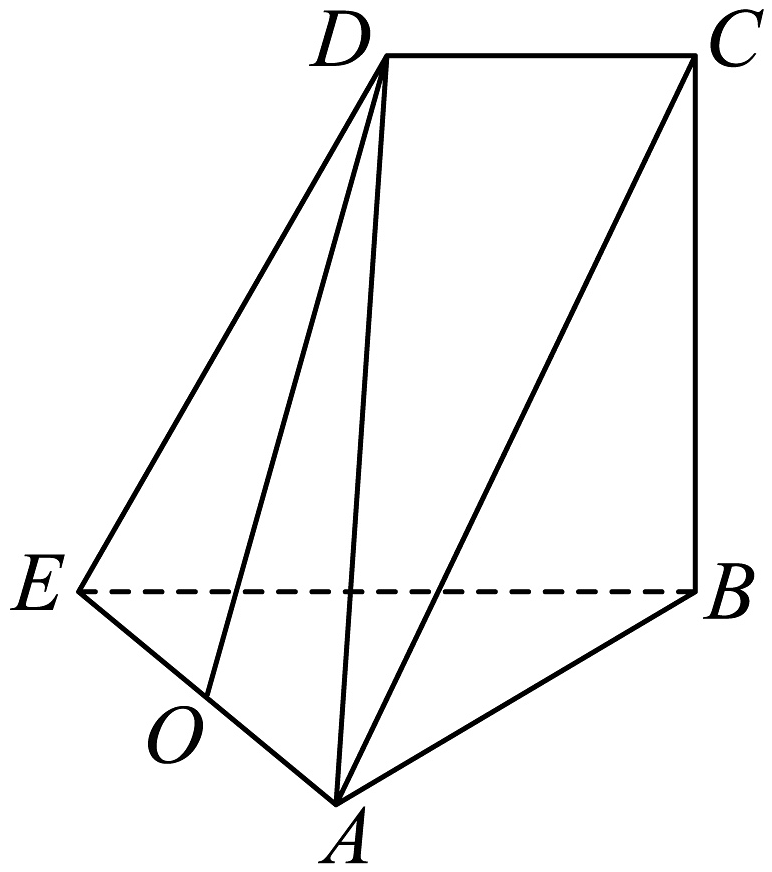 (1)、求证:平面;(2)、在棱上是否存在点 , 使得直线与平面所成角的正弦值为 , 若存在,求的值,若不存在,说明理由
(1)、求证:平面;(2)、在棱上是否存在点 , 使得直线与平面所成角的正弦值为 , 若存在,求的值,若不存在,说明理由 -
20、在中,角的对边分别为 , 且 .(1)、求角的大小;(2)、若 , 角的平分线交于点 , 求线段的长.