-
1、函数 , 无论取何值,函数图象恒过一个定点,则定点坐标为.
-
2、设 , , 则下列不等式一定成立的是( )A、 B、 C、 D、
-
3、下列各组函数中表示同一个函数的是( )A、 , B、 , C、 , D、 ,
-
4、函数的部分图像大致为( )A、
 B、
B、 C、
C、 D、
D、
-
5、设是定义在上的奇函数,且当时, , 则( )A、 B、 C、 D、
-
6、已知集合 , , 则( )A、 B、 C、 D、
-
7、已知函数过点.(1)、求的解析式;(2)、判断在区间上的单调性,并用定义证明.
-
8、已知集合 , ,(1)、若 , 求 , ;(2)、若 , 求实数的取值范围.
-
9、已知函数 , , 求函数的最大值和最小值.
-
10、已知函数 , 则 .
-
11、函数的图象如图所示(图中曲线与直线无限接近,但永不相交),则下列选项正确的有( )
 A、函数的值域为 B、函数的定义域为 C、对 , 都有两个不同的值与之对应 D、当函数(为常数)与函数的图象只有一个交点时,的取值范围为
A、函数的值域为 B、函数的定义域为 C、对 , 都有两个不同的值与之对应 D、当函数(为常数)与函数的图象只有一个交点时,的取值范围为 -
12、某汽车制造厂建造了一个高科技自动化生产车间,据市场分析这个车间产出的总利润(单位:千万元)与运行年数满足二次函数关系,其函数图象如图所示,则这个车间运行( )年时,其产出的年平均利润最大.
 A、 B、 C、 D、
A、 B、 C、 D、 -
13、已知集合 , , 则( )A、 B、 C、 D、
-
14、如图,在四棱锥中,平面 , 底面是边长为2的正方形, , 为棱的中点,
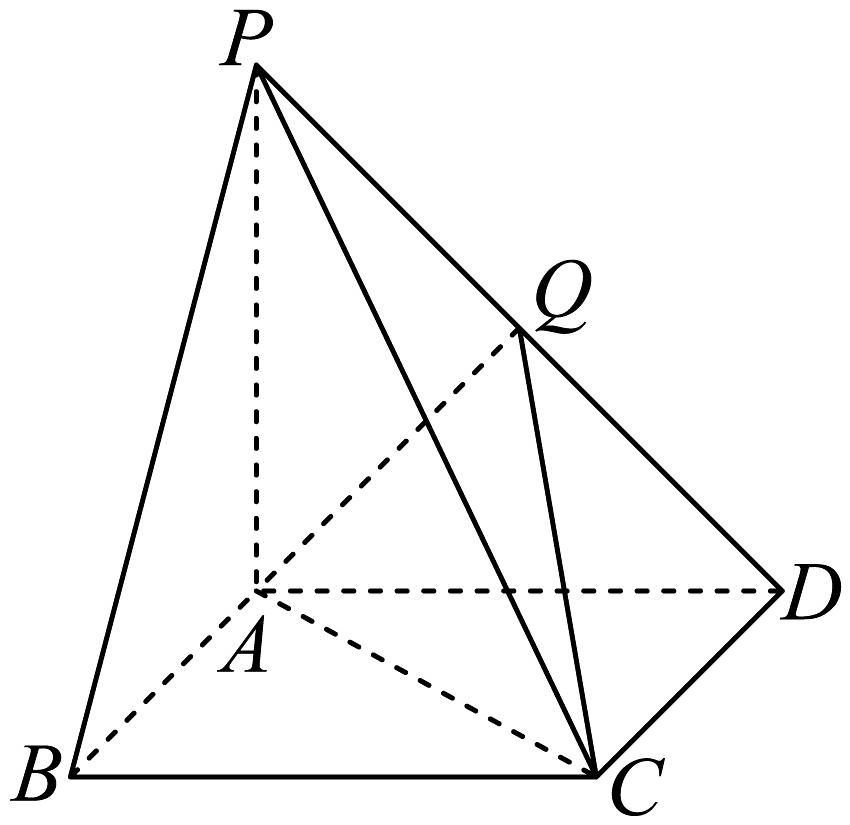 (1)、求证:平面;(2)、直线与平面所成角的正弦值;(3)、点到平面的距离.
(1)、求证:平面;(2)、直线与平面所成角的正弦值;(3)、点到平面的距离. -
15、如图在四面体中,分别是的中点,则( )
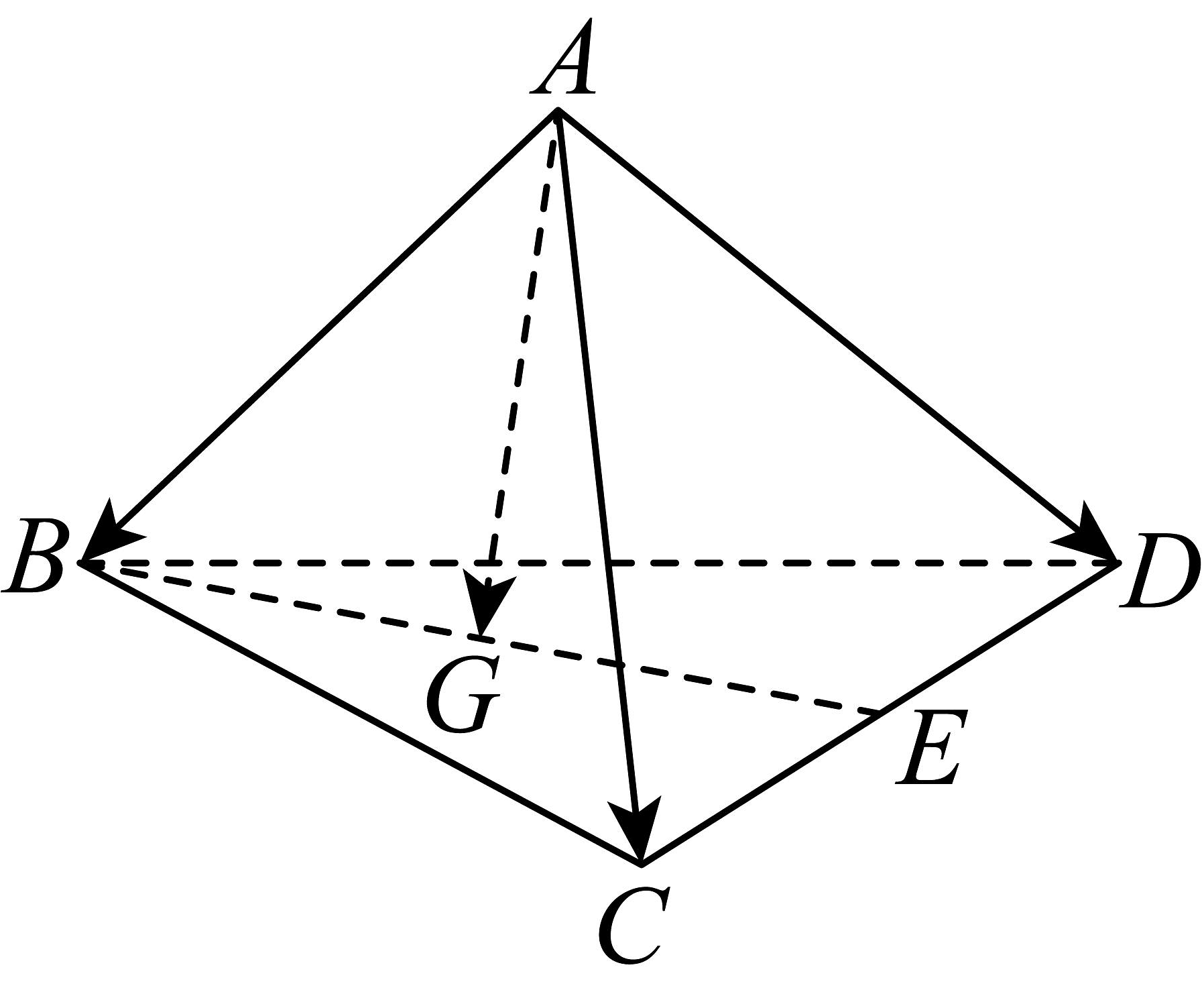 A、 B、 C、 D、
A、 B、 C、 D、 -
16、已知直线的一个方向向量为 , 直线的一个方向向量为 , 若 , 则( )A、 B、3 C、6 D、9
-
17、计算下列各式的值.(1)、;(2)、已知 , 求的值.
-
18、酒驾是严重危害交通安全的违法行为.为了保障交通安全,根据国家有关规定:血液中酒精含量达到的驾驶员即为酒后驾车,及以上认定为醉酒驾车.假设某驾驶员喝了一定量的酒后,其血液中的酒精含量上升到.如果在停止喝酒以后,他血液中酒精含量会以每小时的速度减少,那么他至少经过个(精确到整数)小时才能驾驶?(参考数据)
-
19、已知函数为奇函数.则.
-
20、定义在的函数满足 , 当时, , 则下列说法正确的是( )A、 B、若 , 则 C、函数在上是增函数 D、不等式的解集为