相关试卷
- 高中数学人教新课标A版必修3 第一章 算法初步 1.3算法案例
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.3循环语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.1输入语句、输出语句和赋值语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.1算法与程序框图(包括1.1.1算法的概念,1.1.2程序框图与算法的基本逻辑结构)
- 高中数学人教新课标A版必修3 第三章 概率 3.3几何概型
- 高中数学人教新课标A版必修3 第三章 概率 3.2古典概型
- 高中数学人教新课标A版 必修3 第三章 概率 3.1.3概率的基本性质
- 高中数学人教新课标A版必修3 第三章 概率 3.1.1随机事件的概率,3.1.2概率的意义
- 高中数学人教新课标A版必修3 第二章 统计 2.3变量间的相关关系(包括2.3.1变量间的相关关系,2.3.2两个变量的线性相关)
- 高中数学人教新课标A版必修3 第二章 统计 2.2.2用样本的数字特征估计总体的数字特征
-
1、在如图所示的试验装置中,两个正方形框架 , 的边长都是1,且它们所在平面互相垂直,活动弹子分别在正方形对角线和上移动,且和的长度保持相等,记 , 活动弹子在上移动.
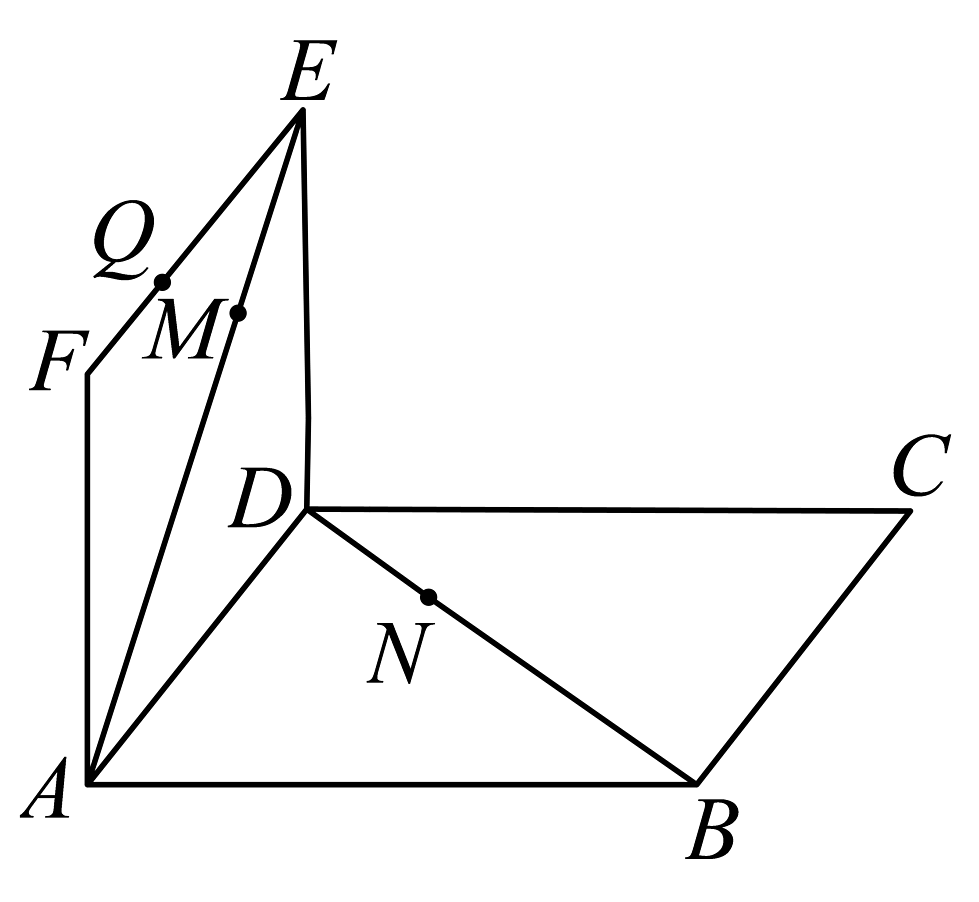 (1)、求证:直线平面;(2)、a为何值时,的长最小?(3)、为上的点,求与平面所成角的正弦值的最大值.
(1)、求证:直线平面;(2)、a为何值时,的长最小?(3)、为上的点,求与平面所成角的正弦值的最大值. -
2、记的内角的对边分别为 , 已知 , 外接圆的半径为R.(1)、求外接圆的面积;(2)、圆经过 , 且与圆关于直线对称,圆被直线截得弦长为8,求直线的方程.
-
3、设直线l的方程为(1)、求证:无论a为何值,直线l必过一定点P;(2)、若直线l分别与x轴正半轴,y轴正半轴交于A,B,当面积最小时,求的周长;(3)、当直线l在两坐标轴上的截距均为整数且斜率为正值时,求直线l的方程.
-
4、已知点 , 设 .(1)、求在方向上的投影向量(用坐标表示);(2)、求 .
-
5、已知P为上的点,过点P作圆O:的切线,切点为M、N,若使得的点P有8个,则m的取值范围是.
-
6、设直线经过点是它的一个方向向量,是直线上任意一点,则向量与共线,根据向量共线的充要条件,存在唯一的实数 , 使 , 即 , 所以 , 我们把上式称为直线的参数方程.若直线的参数方程为(为参数),则其倾斜角为 .
-
7、已知空间向量 , , 共面,则实数的值为 .
-
8、设是空间中两两夹角均为的三条数轴,分别是与轴正方向同向的单位向量,若 , 则把有序数对叫作向量在坐标系中的坐标,则下列结论正确的是( )A、若向量 , 向量 , 则 B、若向量 , 向量 , 则 C、若的最小值为 , 则 D、若向量 , 向量 , 向量 , 则二面角的余弦值为
-
9、古希腊数学家阿波罗尼斯与欧几里得、阿基米德齐名,他发现:“平面内到两个定点A,B的距离之比为定值m(且)的点的轨迹是圆”.人们将这个圆以他的名字命名为阿波罗尼斯圆,简称阿氏圆.在平面直角坐标系xOy中, , , 点P满足 . 设点P的轨迹为C,则下列结论正确的是( )A、轨迹C的方程为 B、轨迹C与圆M:有两条公切线 C、轨迹C与圆O:的公共弦所在直线方程为 D、当A,B,P三点不共线时,射线PO是∠APB的平分线
-
10、下面四个结论中正确的是( )A、若对空间中任一点 , 有 , 则四点共面 B、若 , 则向量的夹角是锐角 C、点关于平面对称的点的坐标是 D、已知向量满足 , 且 , 则
-
11、《九章算术》中,将四个面都为直角三角形的四面体称为鳖臑.在如图所示的鳖臑中,平面 , , , E是BC的中点,H是内的动点(含边界),且平面 , 则的取值范围是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
12、已知不同两点 , 在曲线上,且满足 , 则直线AB斜率的取值范围是( )A、 B、 C、 D、
-
13、如图,在棱长为3的正方体中,点是棱上的一点,且 , 则点到平面的距离为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
14、将一枚骰子先后抛掷两次,若先后出现的点数分别记为a,b,则直线到原点的距离不超过1的概率是( )A、 B、 C、 D、
-
15、如图,在正三棱锥中,点为的重心,点是线段上的一点,且 , 记 , 则( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
16、已知为平面α的法向量, A,B是直线上的两点,则·=0是直线b∥α的( )条件A、必要不充分 B、充分不必要 C、充要 D、既不充分又不必要
-
17、设 , 向量 , 且 , 则( )A、 B、 C、 D、
-
18、如图,在四棱锥中,是以为斜边的等腰直角三角形, , , , 为的中点.
 (1)、证明:平面;(2)、若 , 求平面与平面的夹角的余弦值.
(1)、证明:平面;(2)、若 , 求平面与平面的夹角的余弦值. -
19、某工厂引进了一条生产线,为了解产品的质量情况,现从生产线上随机抽取100件产品,测量其技术参数,得到如图所示的频率分布直方图.
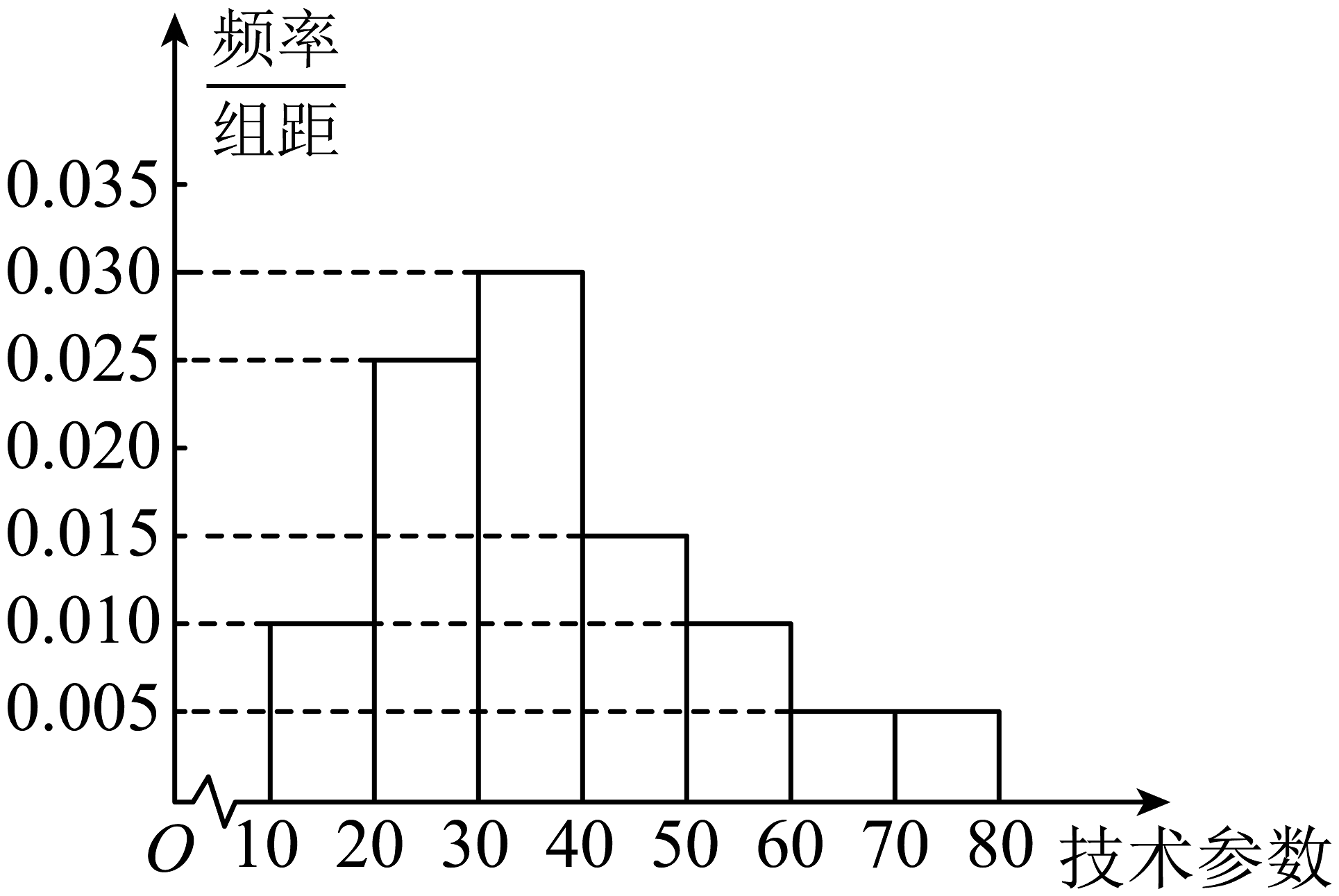 (1)、由频率分布直方图,估计样本技术参数的平均数和75%分位数(精确到0.1);(2)、现从技术参数位于区间 , , 的三组中,采用分层抽样的方法抽取6件产品,再从这6件产品中任选3件产品,记事件“这3件产品中技术参数位于区间内的产品至多1件”,事件“这3件产品中技术参数位于区间内的产品至少1件”,求事件的概率.
(1)、由频率分布直方图,估计样本技术参数的平均数和75%分位数(精确到0.1);(2)、现从技术参数位于区间 , , 的三组中,采用分层抽样的方法抽取6件产品,再从这6件产品中任选3件产品,记事件“这3件产品中技术参数位于区间内的产品至多1件”,事件“这3件产品中技术参数位于区间内的产品至少1件”,求事件的概率. -
20、如图,在几何体中,平面平面.四边形为矩形.在四边形中,.
 (1)、点在线段上,且 , 是否存在实数 , 使得?若存在,求出的值;若不存在,请说明理由.(2)、若为线段的中点,求直线与平面所成角的正弦值.
(1)、点在线段上,且 , 是否存在实数 , 使得?若存在,求出的值;若不存在,请说明理由.(2)、若为线段的中点,求直线与平面所成角的正弦值.