相关试卷
- 高中数学人教新课标A版必修3 第一章 算法初步 1.3算法案例
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.3循环语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.1输入语句、输出语句和赋值语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.1算法与程序框图(包括1.1.1算法的概念,1.1.2程序框图与算法的基本逻辑结构)
- 高中数学人教新课标A版必修3 第三章 概率 3.3几何概型
- 高中数学人教新课标A版必修3 第三章 概率 3.2古典概型
- 高中数学人教新课标A版 必修3 第三章 概率 3.1.3概率的基本性质
- 高中数学人教新课标A版必修3 第三章 概率 3.1.1随机事件的概率,3.1.2概率的意义
- 高中数学人教新课标A版必修3 第二章 统计 2.3变量间的相关关系(包括2.3.1变量间的相关关系,2.3.2两个变量的线性相关)
- 高中数学人教新课标A版必修3 第二章 统计 2.2.2用样本的数字特征估计总体的数字特征
-
1、已知等差数列的前四项和为10,且成等比数列
(1)求数列通项公式
(2)设 , 求数列的前项和
-
2、设函数.(1)、求函数的最小正周期和对称轴;(2)、 , , 分别为内角 , , 的对边,已知 , , 的面积为 , 求的周长.
-
3、若 , 则.
-
4、在中, , , , 为边上一动点,则( )A、 B、当为角的角平分线时, C、当为边中点时, D、若点为内任一点,的最小值为
-
5、已知函数的部分图象如图所示,则( )
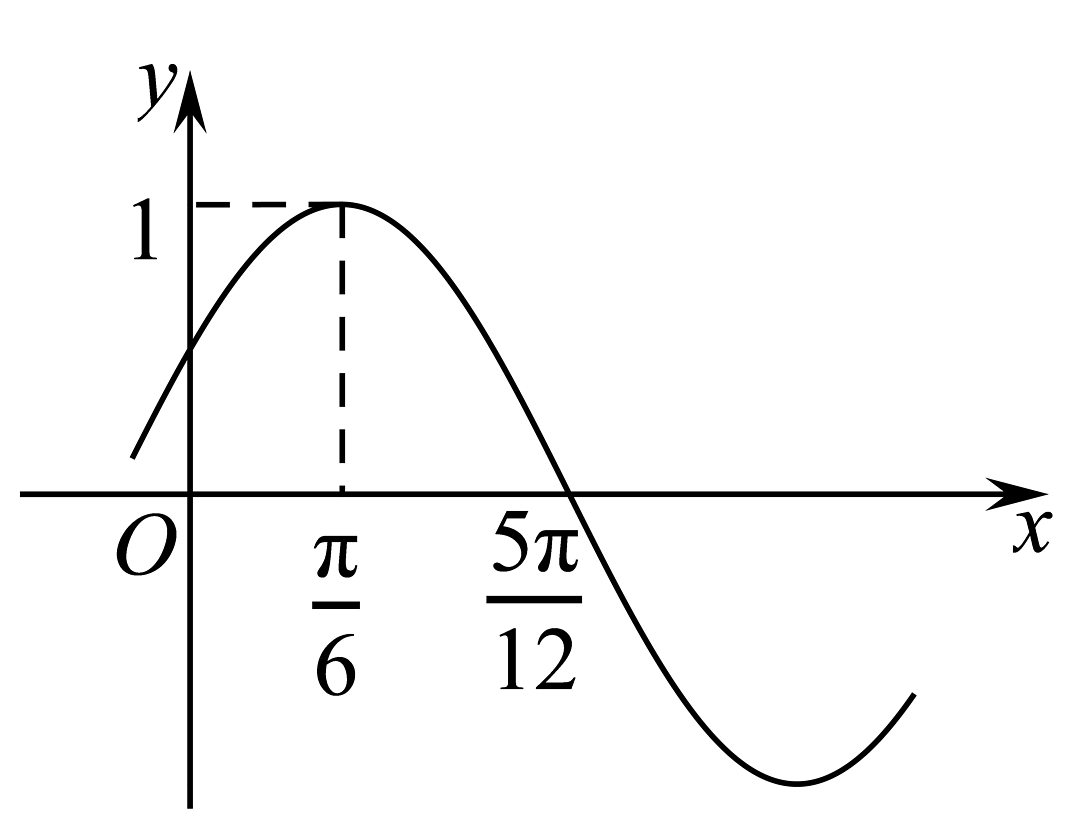 A、的最小正周期为 B、当时,的值域为 C、将函数的图象向右平移个单位长度可得函数的图象 D、将函数的图象上所有点的横坐标伸长为原来的2倍,纵坐标不变,得到的函数图象关于点对称
A、的最小正周期为 B、当时,的值域为 C、将函数的图象向右平移个单位长度可得函数的图象 D、将函数的图象上所有点的横坐标伸长为原来的2倍,纵坐标不变,得到的函数图象关于点对称 -
6、已知 , 则( )A、的虚部为 B、是纯虚数 C、在复平面内所对应的点位于第一象限 D、
-
7、当时,不等式 恒成立,则实数的取值范围为( )A、 B、 C、 D、
-
8、已知 , 则 ( )A、 B、 C、 D、
-
9、若一个圆台的高为 , 母线与底面所成角为 , 上底面半径为 , 则该圆台的侧面积为( )A、 B、 C、 D、
-
10、已知向量 , , 其中 , 若 , 则( )A、40 B、48 C、51 D、62
-
11、已知 , , 则是的( )条件A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分又不必要条件
-
12、若复数满足 , 则( ).A、 B、 C、 D、
-
13、已知集合 , , 则( )A、 B、 C、 D、
-
14、已知抛物线 , 直线交抛物线于两点,(1)、若线段中点的纵坐标为2,求直线的方程;(2)、若抛物线上存在两点关于直线轴对称,求的取值范围.(3)、若存在定点 , 使以为直径的圆上的任意点 , 都满足(为原点),求定点的坐标和的值.
-
15、设 , 则“”是“”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件
-
16、已知动点到直线的距离比它到定点的距离多1(1)、求的方程;(2)、若过点的直线与相交于A,B两点,且 , 求直线的方程.
-
17、已知函数 , 且在上的最小值为0.(1)、求实数的取值范围;(2)、设函数在区间上的导函数为 , 若对任意实数恒成立,则称函数在区间上具有性质.
(i)求证:函数在上具有性质;
(ii)记 , 其中 , 求证:.
-
18、如图,广东省某机器人比赛设计了一个矩形场地ABCD(含边界和内部,A为坐标原点),AD长10米,在AB边上距离A点4米的F处放一只电子狗,在距A点2米的E处放一个机器人,机器人行走速度为v,电子狗行走速度为2v,若电子狗和机器人在场地内沿直线方向同时到达场地内某点M,那么电子狗将被机器人捕获,点M叫“成功点”.
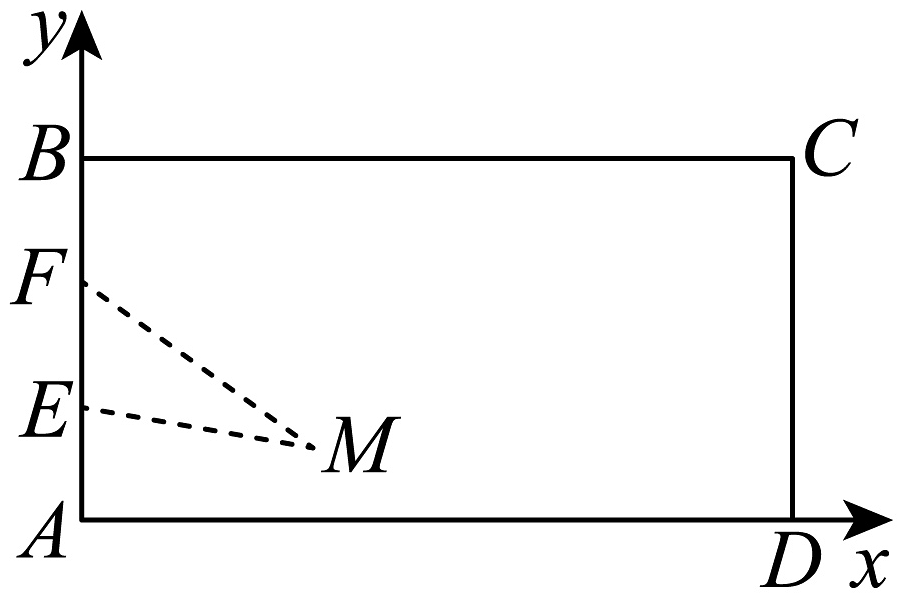 (1)、求在这个矩形场地内“成功点”M的轨迹方程;(2)、若P为矩形场地AD边上的一点,电子狗在线段FP上总能逃脱,求|AP|的取值范围.
(1)、求在这个矩形场地内“成功点”M的轨迹方程;(2)、若P为矩形场地AD边上的一点,电子狗在线段FP上总能逃脱,求|AP|的取值范围. -
19、已知直三棱柱中, , 分别为和的中点,为棱上的动点,.
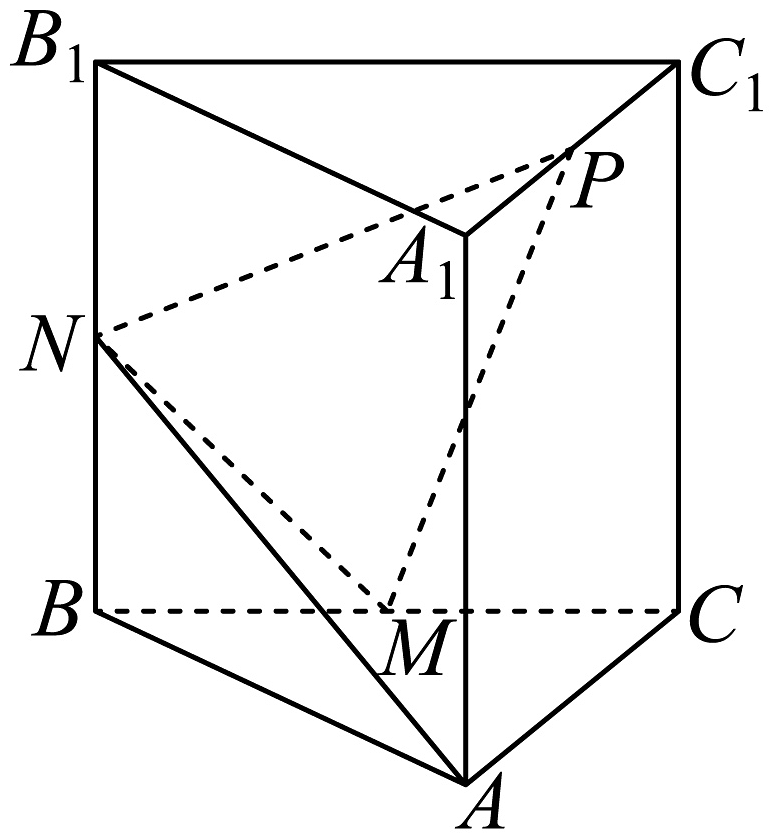 (1)、证明:平面平面;(2)、设 , 是否存在实数 , 使得平面与平面所成的角的余弦值为?
(1)、证明:平面平面;(2)、设 , 是否存在实数 , 使得平面与平面所成的角的余弦值为? -
20、已知数列中 , ,(1)、证明数列 是等比数列;(2)、若数列 的通项公式为 , 求数列 的前n项和.