相关试卷
- 高中数学人教新课标A版必修3 第一章 算法初步 1.3算法案例
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.3循环语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.1输入语句、输出语句和赋值语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.1算法与程序框图(包括1.1.1算法的概念,1.1.2程序框图与算法的基本逻辑结构)
- 高中数学人教新课标A版必修3 第三章 概率 3.3几何概型
- 高中数学人教新课标A版必修3 第三章 概率 3.2古典概型
- 高中数学人教新课标A版 必修3 第三章 概率 3.1.3概率的基本性质
- 高中数学人教新课标A版必修3 第三章 概率 3.1.1随机事件的概率,3.1.2概率的意义
- 高中数学人教新课标A版必修3 第二章 统计 2.3变量间的相关关系(包括2.3.1变量间的相关关系,2.3.2两个变量的线性相关)
- 高中数学人教新课标A版必修3 第二章 统计 2.2.2用样本的数字特征估计总体的数字特征
-
1、已知是曲线上的一点,则下列选项中正确的是( )A、曲线的图象关于原点对称 B、对任意 , 直线与曲线有唯一交点 C、对任意 , 恒有 D、曲线在的部分与轴围成图形的面积小于
-
2、已知抛物线 , 过的焦点作直线 , 若与交于两点, , 则下列结论正确的有( )A、 B、 C、或 D、线段中点的横坐标为
-
3、已知函数的图象关于直线轴对称,且在上没有最小值,则的值为( )A、 B、1 C、 D、2
-
4、已知集合 , 则( )A、 B、 C、 D、
-
5、已知函数的部分图象如图所示,则下列说法正确的是( )
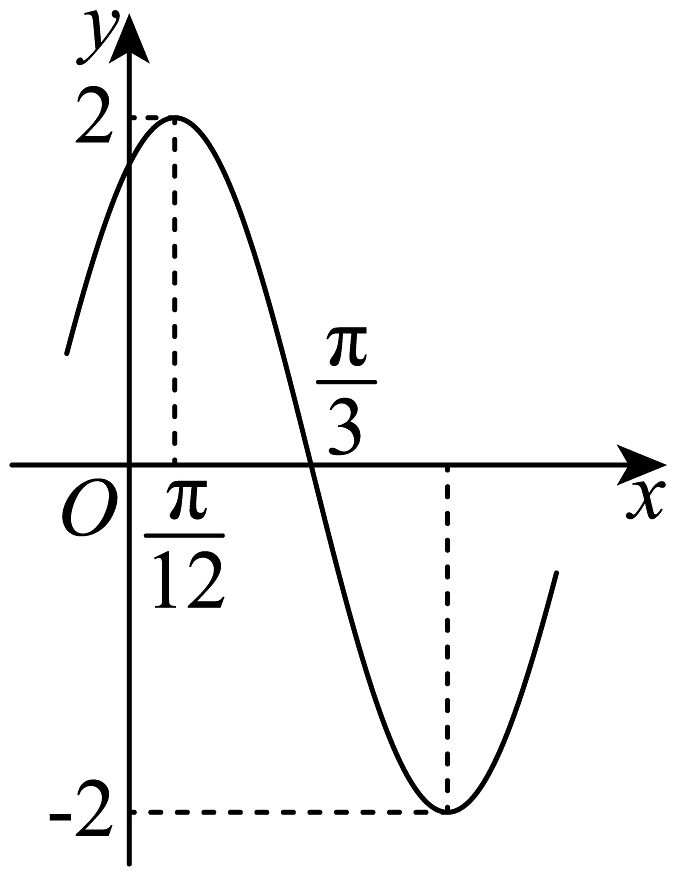 A、 B、函数的图象关于直线对称 C、函数是偶函数 D、将函数图象上所有点的横坐标变为原来的2倍,得到函数的图象
A、 B、函数的图象关于直线对称 C、函数是偶函数 D、将函数图象上所有点的横坐标变为原来的2倍,得到函数的图象 -
6、从出游方式看,春节期间是家庭旅游好时机.某地区消费者协会调查了部分2024年春节以家庭为单位出游支出情况,统计得到家庭旅游总支出(单位:百元)频率分布直方图,如图所示.(同一组中的数据用该组区间的中点值为代表)
 (1)、求的值;(2)、估计家庭消费总支出的第75百分位数.(3)、从和两组中用分层抽样的方法共抽取了6人,再从这6人中随机抽取2人,求所抽取的2人来自同一组的概率.
(1)、求的值;(2)、估计家庭消费总支出的第75百分位数.(3)、从和两组中用分层抽样的方法共抽取了6人,再从这6人中随机抽取2人,求所抽取的2人来自同一组的概率. -
7、如图,正方体的棱长为2,则下列说法正确的是( )
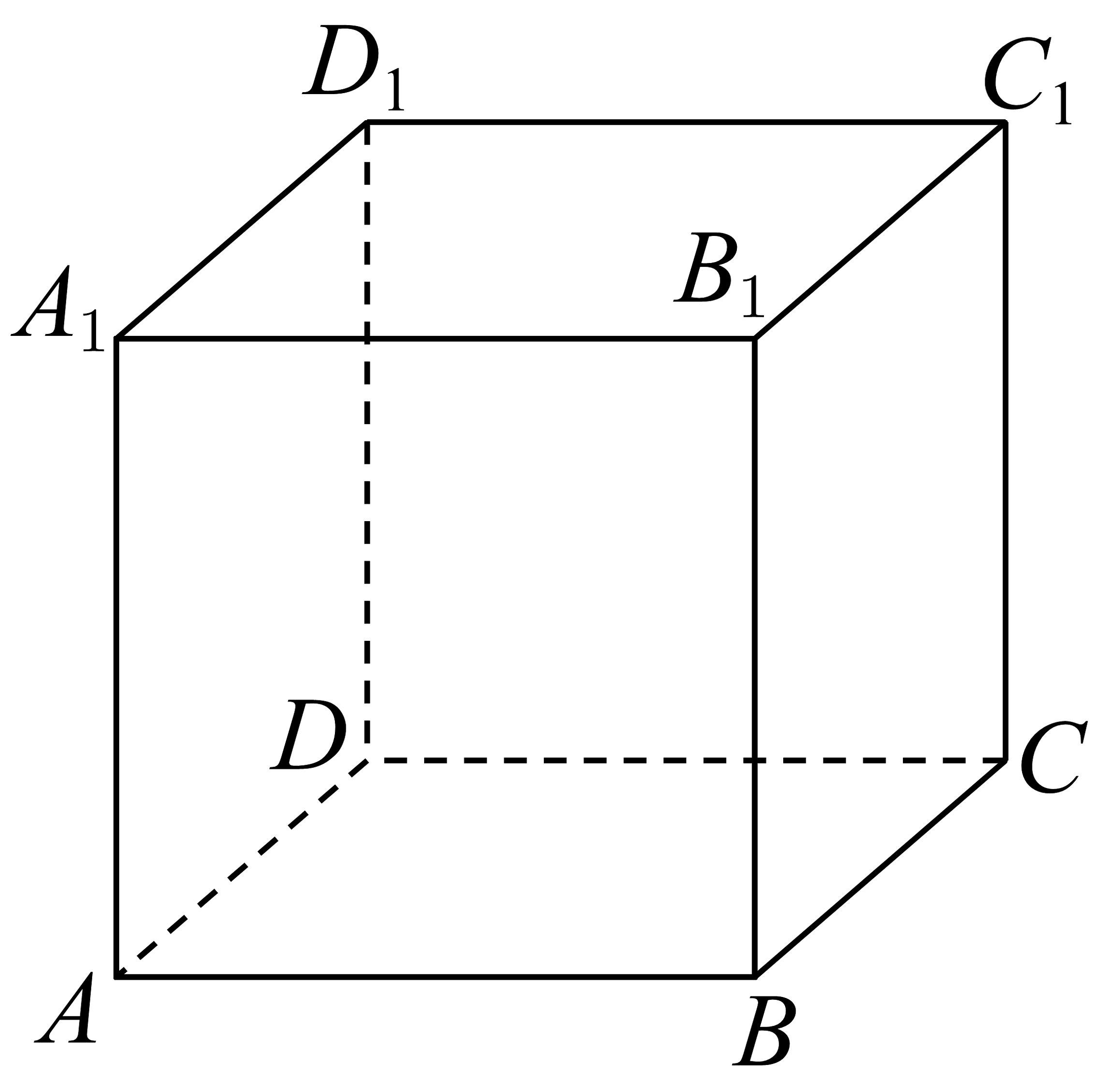 A、直线和所成的角为 B、四面体的体积是 C、点到平面的距离为 D、平面与平面夹角的正弦值为
A、直线和所成的角为 B、四面体的体积是 C、点到平面的距离为 D、平面与平面夹角的正弦值为 -
8、已知非零向量 , , 则“”是“向量”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件
-
9、已知矩形的长为2,宽为1.(如图所示)
 (1)、若E为DC的中点,将矩形沿BE折起,使得平面平面 , 分别求到AB和AD的距离.(2)、在矩形ABCD中,点M是AD的中点、点N是AB的三等分点(靠近A点).沿折痕MN将翻折成 , 使平面平面.又点G,H分别在线段NB,CD上,若沿折痕GH将四边形向上翻折,使C与重合,求线段NG的长.
(1)、若E为DC的中点,将矩形沿BE折起,使得平面平面 , 分别求到AB和AD的距离.(2)、在矩形ABCD中,点M是AD的中点、点N是AB的三等分点(靠近A点).沿折痕MN将翻折成 , 使平面平面.又点G,H分别在线段NB,CD上,若沿折痕GH将四边形向上翻折,使C与重合,求线段NG的长. -
10、若函数满足:对任意正数 , 都有 , 则称函数为“H函数”.(1)、试判断函数与是否为“H函数”,并说明理由;(2)、若函数是“H函数”,求实数a的取值范围;(3)、若函数为“H函数”, , 对任意正数s、t,都有 , , 证明:对任意 , 都有 .
-
11、象棋是中国棋文化之一,也是中华民族的文化瑰宝,源远流长,雅俗共赏.某地举办象棋比赛,规定:每一局比赛中胜方得1分,负方得0分,没有平局.(1)、若甲、乙两名选手进行象棋比赛冠亚军的激烈角逐,每局比赛甲获胜的概率是 , 乙获胜的概率是 , 先得3分者夺冠,比赛结束.
(i)求比赛结束时,恰好进行了3局的概率;
(ii)若前两局甲、乙各胜一局,记表示到比赛结束还需要进行的局数,求的分布列及数学期望;
(2)、统计发现,本赛季参赛选手总得分近似地服从正态分布.若 , 则参赛选手可获得“参赛纪念证书”;若 , 则参赛选手可获得“优秀参赛选手证书”.若共有200名选手参加本次比赛,试估计获得“参赛纪念证书”的选手人数.(结果保留整数)附:若 , 则 , .
-
12、已知数列满足: , .(1)、求数列的通项公式;(2)、对任意 . 将数列中落入区间内的项的个数记为 , 求数列的前m项和 .
-
13、已知函数.
(1)若函数在区间上单调递增,求的取值范围;
(2)设函数 , 若存在 , 使不等式成立,求实数的取值范围.
-
14、如图,四边形为平行四边形, , 若 , 则的值为 .

-
15、如图,点是棱长为2的正方体的表面上一个动点,是线段的中点,则( )
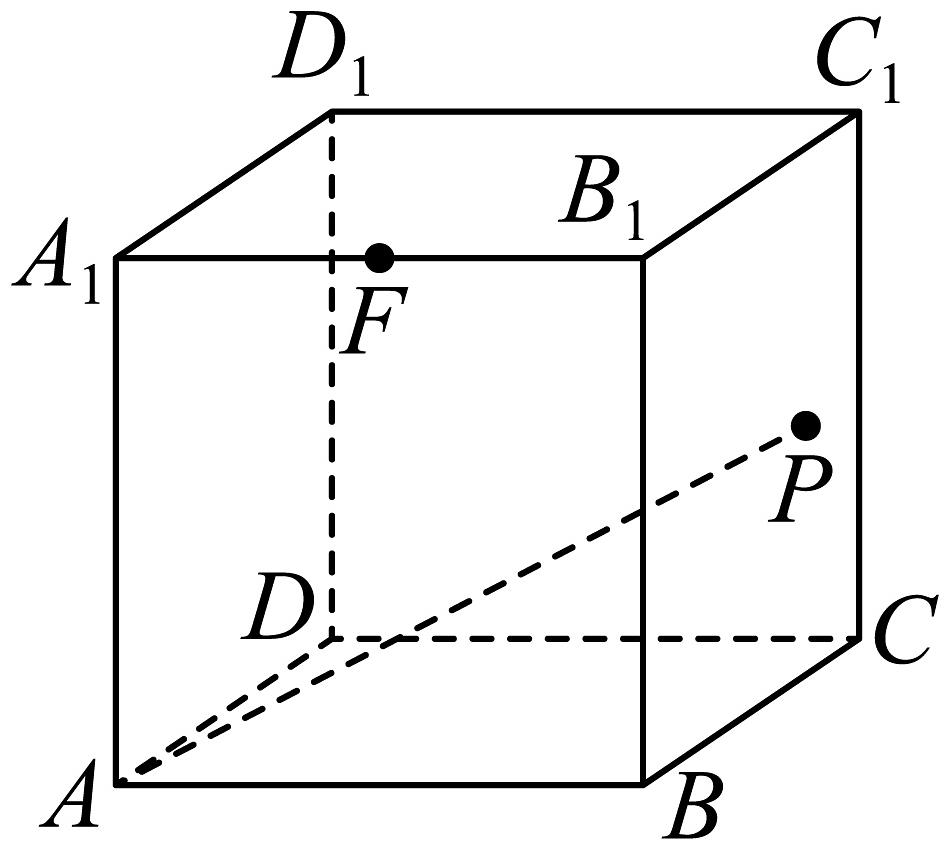 A、若点满足 , 则动点的轨迹长度为 B、三棱锥体积的最大值为 C、当直线与所成的角为时,点的轨迹长度为 D、当在底面上运动,且满足平面时,线段长度最大值为
A、若点满足 , 则动点的轨迹长度为 B、三棱锥体积的最大值为 C、当直线与所成的角为时,点的轨迹长度为 D、当在底面上运动,且满足平面时,线段长度最大值为 -
16、已知函数的定义域为R,且 , , 则( )A、 B、有最小值 C、 D、是奇函数
-
17、定义运算 . 在中,角A,B,C的对边分别为a,b,c,若a,b,c满足 , 则下列结论正确的是( )A、 B、 C、角B的最大值为 D、若 , 则为钝角三角形
-
18、已知函数 , 若当时,恒成立,则实数的取值范围是( )A、 B、 C、 D、
-
19、设椭圆的左,右焦点分别为 , 直线过点 , 若点关于的对称点恰好在椭圆上,且 , 则的离心率为( )A、 B、 C、 D、
-
20、党的二十大报告提出:“深化全民阅读活动.”今天,我们思索读书的意义、发掘知识的价值、强调阅读的作用,正是为了更好地满足人民群众精神文化生活新期待.某市把图书馆、博物馆、美术馆、文化馆四个公共文化场馆面向社会免费开放,开放期间需要志愿者参与协助管理.现有、、、、共5名志愿者,每名志愿者均参与本次志愿者服务工作,每个场馆至少需要一名志愿者,每名志愿者到各个场馆的可能性相同,则、两名志愿者不在同一个场馆的概率为( )A、 B、 C、 D、