相关试卷
- 高中数学人教新课标A版必修3 第一章 算法初步 1.3算法案例
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.3循环语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.1输入语句、输出语句和赋值语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.1算法与程序框图(包括1.1.1算法的概念,1.1.2程序框图与算法的基本逻辑结构)
- 高中数学人教新课标A版必修3 第三章 概率 3.3几何概型
- 高中数学人教新课标A版必修3 第三章 概率 3.2古典概型
- 高中数学人教新课标A版 必修3 第三章 概率 3.1.3概率的基本性质
- 高中数学人教新课标A版必修3 第三章 概率 3.1.1随机事件的概率,3.1.2概率的意义
- 高中数学人教新课标A版必修3 第二章 统计 2.3变量间的相关关系(包括2.3.1变量间的相关关系,2.3.2两个变量的线性相关)
- 高中数学人教新课标A版必修3 第二章 统计 2.2.2用样本的数字特征估计总体的数字特征
-
1、函数在一个周期内的图象如图所示,则( ).
 A、该函数的解析式为 B、该函数图象的对称轴方程为 , C、该函数的单调递增区间是 , D、把函数的图象上所有点的横坐标伸长为原来的倍,纵坐标不变,可得到该函数图象
A、该函数的解析式为 B、该函数图象的对称轴方程为 , C、该函数的单调递增区间是 , D、把函数的图象上所有点的横坐标伸长为原来的倍,纵坐标不变,可得到该函数图象 -
2、“虚数”这个词是世纪著名数学家、哲学家笛卡尔创制的,当时的观念认为这是不存在的数.人们发现即使使用全部的有理数和无理数,也不能解决代数方程的求解问题,像这样最简单的二次方程,在实数范围内没有解.引进虚数概念以后,代数方程的求解问题才得以解决.设是方程的根,则( )A、 B、 C、是该方程的根 D、是该方程的根
-
3、已知“水滴”的表面是一个由圆锥的侧面和部分球面(常称为“球冠”)所围成的几何体.如图所示,将“水滴”的轴截面看成由线段和优弧所围成的平面图形,其中点所在直线与水平面平行,和与圆弧相切.已知“水滴”的“竖直高度”与“水平宽度”(“水平宽度”指的是平行于水平面的直线截轴截面所得线段的长度的最大值)的比值为 , 则( )
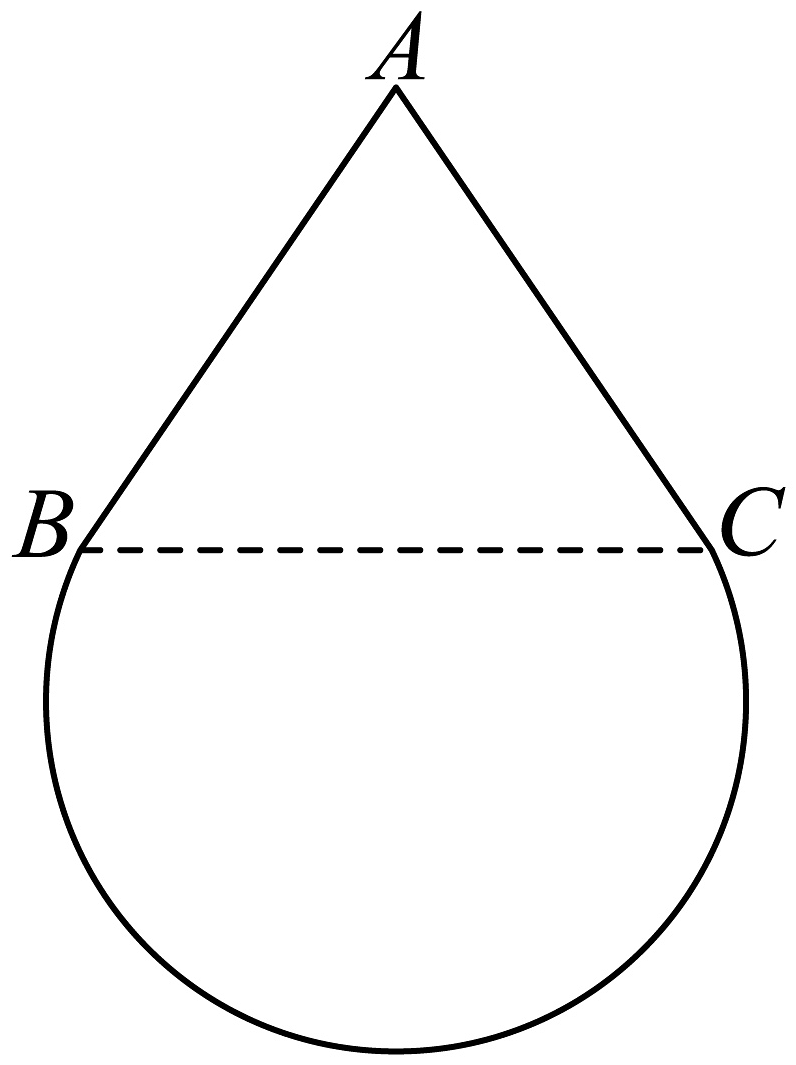 A、 B、 C、 D、
A、 B、 C、 D、 -
4、圆台的上底面半径为1,下底面半径为2,母线长为4.已知P为该圆台某条母线的中点,若一质点从点P出发,绕着该圆台的侧面运动一圈后又回到点P,则该质点运动的最短路径长为( )
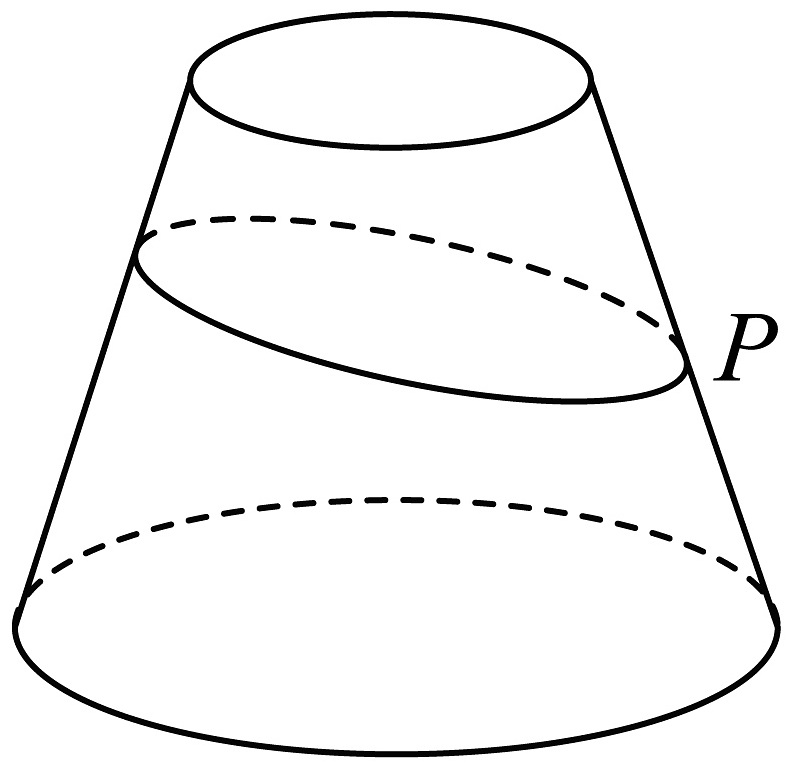 A、 B、6 C、 D、
A、 B、6 C、 D、 -
5、如图,是水平放置的斜二测画法的直观图,的边 , , 则原中角A的角平分线长度是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
6、已知角 , 满足 , , 则的值为( )A、 B、 C、 D、
-
7、已知复数满足 , 则在复平面内对应的点位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限
-
8、若函数的图象上存在个不同点、、、处的切线重合,则称该切线为函数的一条点切线,该函数具有点切线性质.(1)、判断函数 , 的奇偶性并写出它的一条点切线方程(无需理由);(2)、设 , 判断函数是否具有点切线性质,并说明理由;(3)、设 , 证明:对任意的 , , 函数具有点切线性质,并求出所有相应的切线方程.
-
9、椭圆的左右焦点分别为 , 设是第一象限内椭圆上的一点,的延长线交椭圆于点 .
 (1)、若椭圆的离心率 , 求的值;(2)、若 , 求;(3)、若 , 过点的直线与椭圆交于两点,且 , 则当时,判断符合要求的直线有几条,说明理由?
(1)、若椭圆的离心率 , 求的值;(2)、若 , 求;(3)、若 , 过点的直线与椭圆交于两点,且 , 则当时,判断符合要求的直线有几条,说明理由? -
10、如图为正四棱锥为底面的中心.
 (1)、求证:平面 , 平面平面;(2)、设为上的一点, .
(1)、求证:平面 , 平面平面;(2)、设为上的一点, .在下面两问中选一个,
①若 , 求直线与平面所成角的大小.
②已知平面与平面所成锐二面角的大小为 , 若 , 求的长.
-
11、某芯片代工厂生产甲、乙两种型号的芯片,为了解芯片的某项指标,从这两种芯片中各抽取100件进行检测,获得该项指标的频率分布直方图,如图所示:

假设数据在组内均匀分布,以样本估计总体,以事件发生的频率作为相应事件发生的概率.
(1)、求频率分布直方图中x的值并估计乙型芯片该项指标的平均值(同一组中的数据用该组区间的中点值为代表);(2)、已知甲型芯片指标在为航天级芯片,乙型芯片指标在为航天为航天级芯片.现分别采用分层抽样的方式,从甲型芯片指标在内取2件,乙型芯片指标在内取4件,再从这6件中任取2件,求至少有一件为航天级芯片的概率. -
12、已知函数 , 其中(常数且).(1)、若函数的图象过点 , 求关于的不等式的解集;(2)、若存在 , 使得数列是等比数列,求实数的取值范围.
-
13、已知数列不是常数列,前项和为 , . 若对任意正整数 , 存在正整数 , 使得 , 则称是“可控数列”.现给出两个命题:
①若各项均为正整数的等差数列满足公差 , 则是“可控数列”;
②若等比数列是“可控数列”,则其公比 .
则下列判断正确的是( )
A、①与②均为真命题 B、①与②均为假命题 C、①为假命题,②为真命题 D、①为真命题,②为假命题 -
14、在四棱锥中,若 , 则实数组可能是( )A、 B、 C、 D、
-
15、函数 , 则下列命题正确的是( )A、函数是偶函数 B、函数定义域是 C、函数最大值 D、函数的最小正周期为
-
16、在中,“”是“”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件
-
17、已知集合是由函数的图象上两两不相同的点构成的点集,集合 , 其中、 . 若集合中的元素按照从小到大的顺序排列能构成公差为的等差数列,当时,则符合条件的点集的个数为 .
-
18、上海市奉贤区奉城镇的古建筑万佛阁(图1)的屋檐下常系挂风铃(图2),风吹铃动,悦耳清脆,亦称惊鸟铃,一般一个惊鸟铃由铜铸造而成,由铃身和铃舌组成,为了知道一个惊鸟铃的质量,可以通过计算该惊鸟铃的体积,然后由物理学知识计算出该惊鸟铃的质量,因此我们需要作出一些合理的假设:
假设1:铃身且可近似看作由一个较大的圆锥挖去一个较小的圆锥;
假设2:两圆锥的轴在同一条直线上;
假设3:铃身内部有一个挂铃舌的部位的体积忽略不计.
截面图如下(图3),其中 , , , 则制作个这样的惊鸟铃的铃身至少需要千克铜.(铜的密度为)(结果精确到个位)

-
19、申辉中学高一(8)班设计了一个“水滴状”班徽的平面图(如图),徽章由等腰三角形及以弦和劣弧所围成的弓形所组成,其中 , 劣弧所在的圆为三角形的外接圆,圆心为 .

已知 , 外接圆的半径是2,则该图形的面积为 . (用含的表达式表示)
-
20、甲乙两人下棋,每局两人获胜的可能性一样,某一天两人要进行一场三局两胜的比赛,最终胜者赢得100元奖金,第一局比赛甲获胜,后因为有其他事情而中止比赛,则甲应该分元奖金才公平?