相关试卷
- 高中数学人教新课标A版必修3 第一章 算法初步 1.3算法案例
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.3循环语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.1输入语句、输出语句和赋值语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.1算法与程序框图(包括1.1.1算法的概念,1.1.2程序框图与算法的基本逻辑结构)
- 高中数学人教新课标A版必修3 第三章 概率 3.3几何概型
- 高中数学人教新课标A版必修3 第三章 概率 3.2古典概型
- 高中数学人教新课标A版 必修3 第三章 概率 3.1.3概率的基本性质
- 高中数学人教新课标A版必修3 第三章 概率 3.1.1随机事件的概率,3.1.2概率的意义
- 高中数学人教新课标A版必修3 第二章 统计 2.3变量间的相关关系(包括2.3.1变量间的相关关系,2.3.2两个变量的线性相关)
- 高中数学人教新课标A版必修3 第二章 统计 2.2.2用样本的数字特征估计总体的数字特征
-
1、设函数.(1)、当时,求方程的实数解;(2)、当时,
(ⅰ)存在 , 使不等式成立,求k的范围;
(ⅱ)设函数 , 若对任意的 , 总存在 , 使 , 求实数b的取值范围.
-
2、已知函数 , , .(1)、当 , 且时,解关于x的不等式;(2)、若 , , , 求的最小值.
-
3、已知 , 为锐角, , .(1)、求的值;(2)、求的值.
-
4、已知函数和的图象相邻的两个交点为A,B,若 , 则的取值范围为.
-
5、已知函数且在区间上单调递减,则实数的取值范围是.
-
6、若命题“ , 使得”为真命题,则实数a的取值范围是.
-
7、已知函数则下列说法正确的是( )A、函数有3个零点 B、关于x的方程有个不同的解 C、对于实数 , 不等式恒成立 D、在区间内,函数的图象与x轴围成的图形的面积为
-
8、若实数a,b满足 , , 则下列说法正确的为( )A、当时,的最大值为18 B、当时,的最小值为 C、当时,ab的最小值为 D、当时,的最小值为
-
9、若集合 , , 均有恒成立,则t的最大值为( )A、2 B、4 C、8 D、16
-
10、在直角坐标系中,绕原点将x轴的正半轴逆时针旋转角()交单位圆于点A、顺时针旋转角()交单位圆于点B,若点A的纵坐标为 , 且的面积为 , 则点B的纵坐标为( )A、 B、 C、 D、
-
11、若关于x的不等式在区间上有解,则实数m的最小值为( )A、9 B、6 C、 D、5
-
12、已知是定义在上的奇函数,且在上单调递减,设 , 则( )A、 B、 C、 D、
-
13、已知集合 , , 则( )A、 B、 C、 D、
-
14、如图,空间四边形中, , , , 点在上, , 点为中点,则等于( )
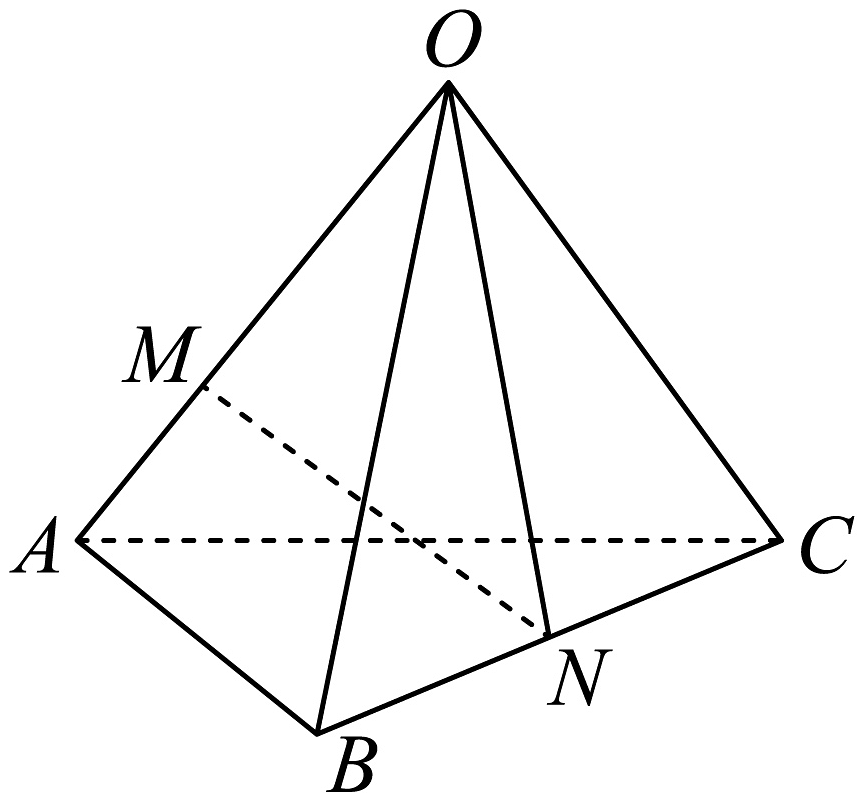 A、 B、 C、 D、
A、 B、 C、 D、 -
15、如图,在平行四边形中, , , , 为中点,且 , .设 , .
 (1)、当时,用 , 表示 , ;(2)、若 , 求实数的值;(3)、求的取值范围.
(1)、当时,用 , 表示 , ;(2)、若 , 求实数的值;(3)、求的取值范围. -
16、已知函数.(1)、求的值域;(2)、求在上所有实数根的和.
-
17、如图,设E、F、G分别是正方体的共点的三条棱、、的中点,过这三个点的平面截正方体得到的一个“角”是四面体. 设正方体的棱长为1.
 (1)、在四面体中,求顶点到底面的距离;(2)、如果将正方体按照题设的方法截去八个“角”,那么剩余的多面体有几个顶点、几条棱、几个面?并求这个剩余多面体的表面积与体积.
(1)、在四面体中,求顶点到底面的距离;(2)、如果将正方体按照题设的方法截去八个“角”,那么剩余的多面体有几个顶点、几条棱、几个面?并求这个剩余多面体的表面积与体积. -
18、已知的内角的对应边分别为 , 且 .(1)、求角A;(2)、若的面积为 , 周长为15,求 .
-
19、若 , 则.
-
20、已知复数满足: , 则.