相关试卷
- 高中数学人教新课标A版必修3 第一章 算法初步 1.3算法案例
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.3循环语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.1输入语句、输出语句和赋值语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.1算法与程序框图(包括1.1.1算法的概念,1.1.2程序框图与算法的基本逻辑结构)
- 高中数学人教新课标A版必修3 第三章 概率 3.3几何概型
- 高中数学人教新课标A版必修3 第三章 概率 3.2古典概型
- 高中数学人教新课标A版 必修3 第三章 概率 3.1.3概率的基本性质
- 高中数学人教新课标A版必修3 第三章 概率 3.1.1随机事件的概率,3.1.2概率的意义
- 高中数学人教新课标A版必修3 第二章 统计 2.3变量间的相关关系(包括2.3.1变量间的相关关系,2.3.2两个变量的线性相关)
- 高中数学人教新课标A版必修3 第二章 统计 2.2.2用样本的数字特征估计总体的数字特征
-
1、(1)已知是一次函数,且满足 , 求;
(2)已知 , 求;
(3)已知函数 , 求;
-
2、已知集合.(1)、若 , 求 , ;(2)、若 , 求的取值范围.
-
3、数学学习过程中,要时刻记得这些注意点:遇到集合注意空集,遇到函数注意定义域,遇到含参方程要找定点,遇到向量要注意零向量,函数(且)的图象必过定点.
-
4、2024年10月21日,第52个梅森素数被发现,这也是迄今为止发现的最大素数.集合以这52个梅森素数为元素,其非空真子集有个.
-
5、已知函数 , 恒成立,则的取值可以为( )A、 B、2 C、5 D、8
-
6、已知函数图象经过点 , 则下列命题正确的有( )A、函数为增函数 B、函数为偶函数 C、若 , 则 D、若 , 则
-
7、已知实数a,b,c满足 , 则下列说法正确的是( )A、 B、 C、 D、
-
8、已知定义在上函数的图象是连续不断的,且满足以下条件:①;② , 当时,都有;③.则下列选项不成立的是( )A、 B、若 , 则 C、若 , 则 D、 , 使得
-
9、某食品的保鲜时间(单位:小时)与储藏温度(单位:℃)满足函数关系(…为自然对数的底数, , 为常数).若该食品在30℃的保鲜时间是18小时,在20℃的保鲜时间是36小时,则该食品在0℃的保鲜时间是( )A、54小时 B、72小时 C、108小时 D、144小时
-
10、已知函数 , 且的最大值为 , 则实数的取值范围是( )A、 B、 C、 D、
-
11、函数的图象大致是( )A、
 B、
B、 C、
C、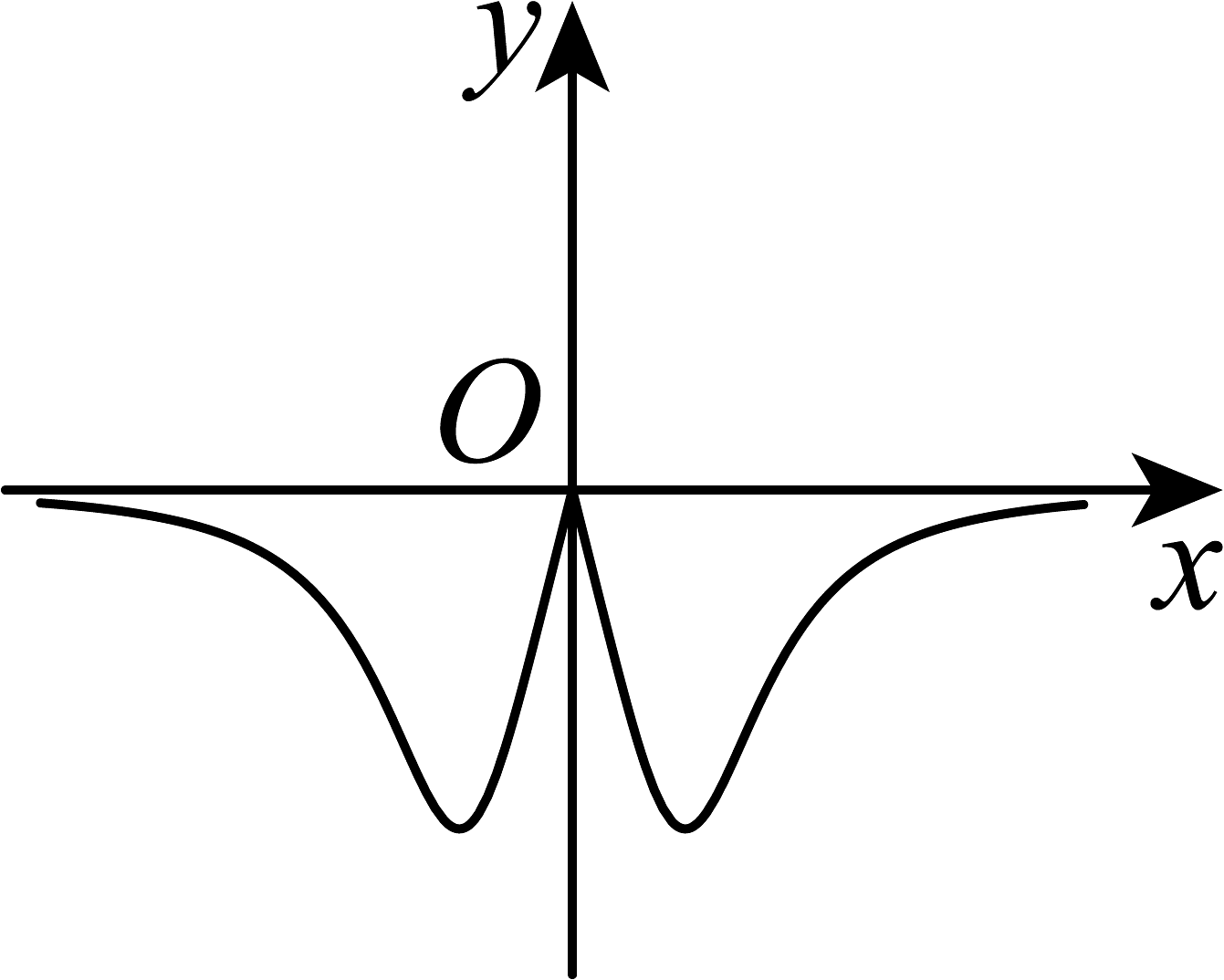 D、
D、
-
12、下列函数中,在上是增函数的是( )A、 B、 C、 D、
-
13、已知函数 , 则的定义域是( )A、 B、 C、 D、
-
14、命题“”的否定是( )A、 B、 C、 D、
-
15、已知集合 , 则( )A、 B、 C、 D、
-
16、在复数范围内方程的一个根为 , 则.
-
17、已知一组数据6,13,14,15,18,13,则特征量为13的是( )A、极差 B、众数 C、中位数 D、第40百分位数
-
18、设为椭圆的左,右焦点,已知点在椭圆上,点为椭圆上的动点,且面积的最大值为2.(1)、求椭圆的方程;(2)、过作斜率为1的直线与椭圆交于两点,求的面积.(3)、黄金分割的比例被认为是最能引起美感的比例,在艺术和设计中广泛应用.若椭圆上一动点到其焦点距离的最小值与最大值之比为黄金分割比的平方,即 , 则称此椭圆为“完美椭圆”.现有一簇椭圆均是“完美椭圆”,其中便是(1)中的椭圆.另一方面,若在椭圆上任取一点 , 以为切点作椭圆的切线与直线且交于点 , 以为直径作圆,设此圆恒过椭圆的右顶点 , 求证:.
-
19、已知双曲线的中心为坐标原点,右焦点为 , 且过点 .(1)、求双曲线的标准方程;(2)、已知点 , 过点的直线与双曲线的左、右两支分别交于点 , 直线与双曲线交于另一点 , 设直线的斜率分别为 .
(i)求证:为定值;
(ii)求证:直线过定点,并求出该定点的坐标.
-
20、如图,在四棱锥中,底面满足 , 底面 , 且.
 (1)、求证:平面;(2)、求平面与平面的夹角的余弦值.
(1)、求证:平面;(2)、求平面与平面的夹角的余弦值.