相关试卷
- 高中数学人教新课标A版必修3 第一章 算法初步 1.3算法案例
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.3循环语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.1输入语句、输出语句和赋值语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.1算法与程序框图(包括1.1.1算法的概念,1.1.2程序框图与算法的基本逻辑结构)
- 高中数学人教新课标A版必修3 第三章 概率 3.3几何概型
- 高中数学人教新课标A版必修3 第三章 概率 3.2古典概型
- 高中数学人教新课标A版 必修3 第三章 概率 3.1.3概率的基本性质
- 高中数学人教新课标A版必修3 第三章 概率 3.1.1随机事件的概率,3.1.2概率的意义
- 高中数学人教新课标A版必修3 第二章 统计 2.3变量间的相关关系(包括2.3.1变量间的相关关系,2.3.2两个变量的线性相关)
- 高中数学人教新课标A版必修3 第二章 统计 2.2.2用样本的数字特征估计总体的数字特征
-
1、已知函数 , 则( )A、函数的图象关于点对称 B、函数的最小正周期为 C、函数在区间上有且仅有一个零点 D、将函数的图象向左平移个单位长度后,得到函数的图象
-
2、如图,从一个半径为的圆形纸板中剪出一块最大的正三角形纸板,并将此正三角形纸板折叠成一个正四面体,则该正四面体外接球的表面积为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
3、已知线段的长度为4,动点与点的距离是它与点的距离的倍,则面积的最大值为( )A、 B、8 C、 D、
-
4、关于的方程对应的曲线不可能是( )A、
 B、
B、 C、
C、 D、
D、
-
5、已知为锐角,若 , 则( )A、 B、 C、 D、
-
6、甲、乙两位学生的5次化学考试成绩如下表:
学生
第一次
第二次
第三次
第四次
第五次
甲
87
91
90
89
99
乙
89
90
91
88
92
下列结论正确的是( )
A、甲的极差小于乙的极差 B、乙的平均数大于甲的平均数 C、乙的成绩比甲的成绩更稳定 D、甲的中位数小于乙的中位数 -
7、记等差数列的前项和为 , 若 , 则( )A、13 B、45 C、65 D、130
-
8、若复数 , 则( )A、 B、 C、 D、4
-
9、已知集合 , 则( )A、 B、 C、 D、
-
10、如图,三棱锥中, , 平面平面 , , , 为棱的中点,为棱上的点.
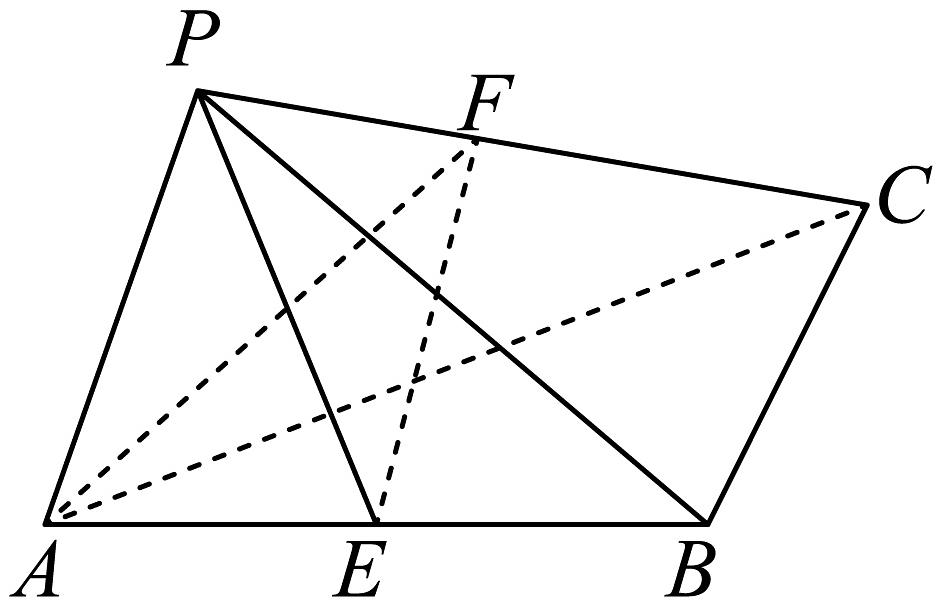 (1)、证明:平面;(2)、若二面角的正弦值为 , 求点到平面的距离.
(1)、证明:平面;(2)、若二面角的正弦值为 , 求点到平面的距离. -
11、已知函数在上单调,且 , 则的最大值为 .
-
12、已知等比数列的前项和为 , 若 , 则.
-
13、如图,圆柱的底面直径为3,母线长为4, , 分别为该圆柱的上、下底面的直径,且 , 则三棱锥的体积是( )
 A、24 B、18 C、12 D、6
A、24 B、18 C、12 D、6 -
14、药房里有若干味药.药剂师用这些药配成22副药方,每副药方中恰有5味药,从中任选的三味药都恰好只包含在某一副药方中.(1)、药房中共有几味药?(2)、药物分为烈性药和非烈性药,要求每副药方中至少有一味是烈性药.
(i)假设药房中有7味烈性药,证明:全部药方中一定有一副药方至少含有4味烈性药;
(ii)证明:全部药方中一定有一副药方至少含有4味烈性药.
-
15、已知数列 , 满足 , 记 .(1)、求数列的通项公式;(2)、求证:;(3)、设数列的前n项和为 , 证明: .
-
16、小明参加一个抽纸牌游戏,规则如下:有九张质地完全相同的纸牌,其中有一张大王牌,其余四种花色为:红桃、黑桃、方块、梅花各2张.逐次从9张牌中不放回地随机抽取一张纸牌,每次抽牌后,都往牌堆中加入一张新的大王牌.(1)、求小明在前两次抽牌中只抽到一张大王牌的情况下,第三次抽牌抽到红桃牌的概率.(2)、抽牌过程中,若抽到大王牌,则宣告游戏结束:若累计抽到两张花色相同的纸牌,也宣告游戏结束;否则游戏继续.用X表示小明在游戏中一共抽到的纸牌数,求X的分布列.
-
17、已知正项等比数列的前n项和为 , 且 .(1)、求数列的通项公式;(2)、若数列满足 , 求数列的前n项和 .
-
18、已知函数(为自然对数的底数).(1)、当时,求曲线在处的切线方程;(2)、若在区间上单调递增,求a的取值范围.
-
19、已知实数 , 且函数 , 则函数的最小值为 .
-
20、将1,2,3,4,5,6这6个数填入图所示的格子中,要求每个数字都要填入,且每个格子只能填一个数,其中1与2相邻(有公共边的两格子称为相邻)的不同的填法有种(结果用数字作答).
