版本：

全部人教A版（2019）人教B版（2019）北师大版（2019）苏教版（2019）上教版（2020）人教新课标A版人教新课标B版苏教版北师大版湘教版沪教版人教版（旧版）

相关试卷

1、2022年夏天，重庆遭遇了极端高温天气，某空调厂家加大力度促进生产.生产某款空调的固定成本是1000万元，每生产 $x$ 千台，需另投入成本 $R (x)$ （单位：万元）， $R (x) = \{\begin{cases} \frac{1}{2} x^{2} + 450 x (1 \leq \leq 60) \\ 510 x + \frac{36000}{x - 10} - 3000 (60 < x \leq 100) \end{cases}$ ，生产的空调能全部销售完，每台空调平均售价5千元．

(1)、写出年利润 $P (x)$ （单位：万元）关于年产量x（单位：千台）的关系式；

(2)、当年产量为多少千台时，这款空调的年利润最大？最大为多少？

查看解析
2、若函数 $f (x) = (x^{2} - 2 x) (x^{2} + a x + b)$ 的图象关于 $x = - 2$ 对称，则 $f (x)$ 的最小值为.

查看解析
3、设函数 $f (x) = x^{2024} - \frac{1}{|x|} + 5$ ，则不等式 $f (x - 1) < 5$ 的解集为.

查看解析
4、已知函数 $y = f (x)$ 是定义在 $[- 1, 1]$ 上的奇函数，当 $x > 0$ 时， $f (x) = x (x - 1)$ ，则下列说法正确的是（）

A、函数 $y = f (x)$ 与x轴有2个交点 B、当 $x < 0$ 时， $f (x) = - x (x + 1)$ C、不等式 $f (x) < 0$ 的解集是 $(0, 1)$ D、 $\forall x_{1}, x_{2} \in [- 1, 1]$ ，都有 $|f (x_{1}) - f (x_{2})| \leq \frac{1}{2}$

查看解析
5、已知关于x的不等式 $a x^{2} + b x + c \geq 0$ 的解集为 $\{x |x \leq - 3$ 或 $x \geq 4\}$ ，则下列说法正确的是（）

A、 $a > 0$ B、不等式 $b x + c < 0$ 的解集为 $\{x| x > - 12\}$ C、不等式 $c x^{2} - b x + a < 0$ 的解集为 $\{x |x < - \frac{1}{4}$ 或 $x > \frac{1}{3}\}$ D、 $a + b + c > 0$

查看解析
6、若函数 $f (x) {= a x}^{2} + b x + c (a \neq 0)$ 在区间 $(2, + \infty)$ 上是单调函数，则实数 $\frac{b}{a}$ 的取值范围是（）

A、 $(- 4 ， + \infty)$ B、 $[- 4 ， + \infty)$ C、 $(- \infty ， - 4]$ D、 $(- \infty ， - 4)$

查看解析
7、已知函数 $f (x)$ 的定义域是 $(0, + \infty)$ ，满足 $f (2) = 1$ 且对于定义域内任意x，y都有 $f (x y) = f (x) + f (y)$ 成立，那么 $f (2) + f (4)$ 的值为（）

A、1 B、2 C、3 D、4

查看解析
8、已知函数f（x）是定义域为R的奇函数，且f（x）＝f（4﹣x），当﹣2≤x＜0时，f（x） $= \frac{1}{x}$ ，则f（ $\frac{7}{2}$ ）＝（）

A、﹣2 B、 $- \frac{2}{7}$ C、 $\frac{2}{7}$ D、2

查看解析
9、已知函数 $f (x) = \{\begin{cases} x^{2}, x \geq 0 \\ - x, x < 0 \end{cases}$ ，则 $f [f (- 2)] =$ （）

A、 $2$ B、 $- 4$ C、 $4$ D、 $16$

查看解析
10、设 $a$ 为实数，则“ $a \geq \frac{1}{a^{2}}$ ”是“ $a^{2} \geq \frac{1}{a}$ ”的（）

A、充分不必要条件 B、必要不充分条件 C、充分必要条件 D、既不充分也不必要条件

查看解析
11、已知集合 $A = {x | y = 2 x - 1}$ ，集合 $B = {y | y = x^{2}}$ ，则集合 $A \cap B =$ （）

A、 $(1, 1)$ B、 $[0, + \infty)$ C、 ${(1, 1)}$ D、 $(0, + \infty)$

查看解析
12、已知函数 $f (x) = | x - 1 |$ ．
$(1)$ 解不等式 $f (2 x) + f (x + 4) \geq 6$ ；
$(2)$ 若a、 $b \in R$ ， $| a | < 1$ ， $| b | < 1$ ，证明： $f (a b) > f (a - b + 1)$ ．

查看解析
13、选修4-4：坐标系与参数方程
在平面直角坐标系 $x O y$ 中，直线 $l$ 的参数方程为 $\{\begin{array}{l} x = - 2 + \frac{1}{2} t \\ y = \frac{\sqrt{3}}{2} t \end{array}$ (t为参数) ，以坐标原点为极点， $x$ 轴正半轴为极轴，建立极坐标系，曲线 $C_{1}$ 的极坐标方程为 $ρ = \sqrt{6}$ .

(1)、写出直线 $l$ 的普通方程和曲线 $C_{1}$ 的参数方程；

(2)、若将曲线 $C_{1}$ 上各点的横坐标缩短为原来的 $\frac{\sqrt{6}}{6}$ 倍，纵坐标缩短为原来的 $\frac{\sqrt{2}}{2}$ 倍，得到曲线 $C_{2}$ ，设点 $P$ 是曲线 $C_{2}$ 上任意一点，求点 $P$ 到直线 $l$ 距离的最小值.

查看解析
14、已知椭圆 $C : \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的离心率为 $\frac{\sqrt{5}}{5}$ ，以椭圆的顶点为顶点的四边形面积为 $4 \sqrt{5}$ .

(1)、求椭圆 $C$ 的标准方程；

(2)、我们称圆心在椭圆 $C$ 上运动且半径为 $\frac{\sqrt{a^{2} + b^{2}}}{3}$ 的圆是椭圆 $C$ 的“环绕圆”.过原点 $O$ 作椭圆 $C$ 的“环绕圆”的两条切线，分别交椭圆 $C$ 于 $A, B$ 两点，若直线 $O A, O B$ 的斜率存在，并记为 $k_{1}, k_{2}$ ，求 $k_{1} k_{2}$ 的取值范围.

查看解析
15、已知平面 $α$ 与平面 $β$ 是空间中距离为1的两平行平面， $A B \subset α$ ， $C D \subset β$ ，且 $A B = C D = 2$ ， $A B$ 和 $C D$ 的夹角为 $60 °$ .

(1)、证明：四面体 $A B C D$ 的体积为定值；

(2)、已知异于 $C$ 、 $D$ 两点的动点 $P \in β$ ，且 $P$ 、 $A$ 、 $B$ 、 $C$ 、 $D$ 均在半径为 $\frac{\sqrt{5}}{2}$ 的球面上.求点 $P$ 到直线 $A B$ 的距离的取值范围.

查看解析
16、已知函数 $f (x) = a x^{2} - ln x, a \in R$ .

(1)、讨论函数 $f (x)$ 的单调性；

(2)、设 $a > 0, g (x) = f (x) + b x$ ，且 $x = 1$ 是 $g (x)$ 的极值点，证明： $2 b +ln a \leq 1 - 2 \ln 2$ .

查看解析
17、如图，在四边形 $A B C D$ 中，已知点C关于直线BD的对称点 $C'$ 在直线AD上， $∠ C B D = ∠ C D B = 30 °$ ， $∠ A C D = 75 °$ ．

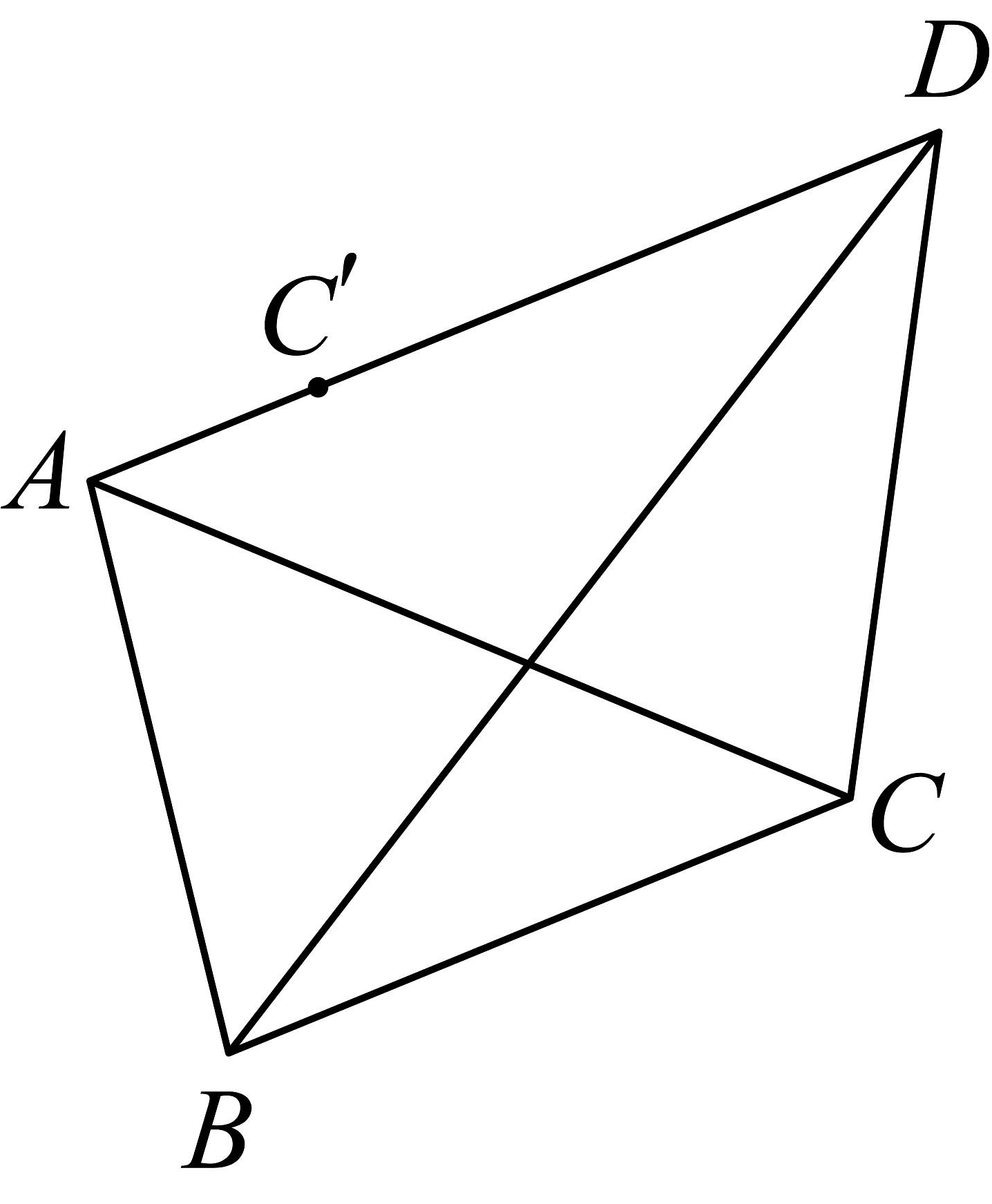(1)、求 $\frac{\sin ∠ B A C}{\sin ∠ A B C}$ 的值；

(2)、设AC=3，求 $A B^{2}$ ．

查看解析
18、成都石室中学生物基地里种植了一种观赏花卉，这种观赏花卉的高度（单位：cm）介于 $[15, 25]$ 之间，现对生物基地里部分该种观赏花卉的高度进行测量，所得数据统计如下图所示.

(1)、求 $a$ 的值；

(2)、若从高度在 $[15, 17)$ 和 $[17, 19)$ 中分层抽样抽取5株，再在这5株中随机抽取2株，求抽取的2株高度均在 $[17, 19)$ 内的概率.

查看解析
19、已知函数 $f (x)$ 的定义域为 $R$ ，对于任意实数 $x, y$ 均满足 $f (\frac{x + 2 y}{3}) = \frac{f (x) + 2 f (y)}{3}$ ，若 $f (2) = 1$ ， $f (5) = 10$ ，则 $f (724) =$ .

查看解析
20、若复数 $z = \frac{1}{2} + \frac{\sqrt{3}}{2} i$ （ $i$ 为虚数单位），则 $\bar{z} \cdot z^{2} =$ .

查看解析

上一页 636 637 638 639 640 下一页跳转