相关试卷
- 高中数学人教新课标A版必修3 第一章 算法初步 1.3算法案例
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.3循环语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.1输入语句、输出语句和赋值语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.1算法与程序框图(包括1.1.1算法的概念,1.1.2程序框图与算法的基本逻辑结构)
- 高中数学人教新课标A版必修3 第三章 概率 3.3几何概型
- 高中数学人教新课标A版必修3 第三章 概率 3.2古典概型
- 高中数学人教新课标A版 必修3 第三章 概率 3.1.3概率的基本性质
- 高中数学人教新课标A版必修3 第三章 概率 3.1.1随机事件的概率,3.1.2概率的意义
- 高中数学人教新课标A版必修3 第二章 统计 2.3变量间的相关关系(包括2.3.1变量间的相关关系,2.3.2两个变量的线性相关)
- 高中数学人教新课标A版必修3 第二章 统计 2.2.2用样本的数字特征估计总体的数字特征
-
1、已知 , , , 则.
-
2、已知函数为奇函数,则实数的值为.
-
3、已知函数 , 则下列结论正确的是( )A、的图象关于轴对称 B、的图象关于点对称 C、的图象关于直线对称 D、是的极大值点
-
4、已知 , 则下列说法正确的是( )A、若 , 则 B、若 , 则 C、若 , , 则的最大值为 D、 , , 使得
-
5、如果关于的不等式的解集为 , 那么下列数值中,可取到的数为( )A、 B、0 C、1 D、2
-
6、已知直线是函数图象的任意两条对称轴,且的最小值为 , 则的单调递增区间是( )A、 B、 C、 D、
-
7、已知(且)是上的奇函数,且(1)、求的解析式;(2)、把区间等分成份,记等分点的横坐标依次为 , , 记 , 是否存在正整数n,使不等式有解?若存在,求出所有n的值,若不存在,说明理由;(3)、函数在区间上的值域是 , 求的取值范围.
-
8、如图,在四棱锥中,底面是正方形,侧棱底面 , , 是的中点,作交于点 .
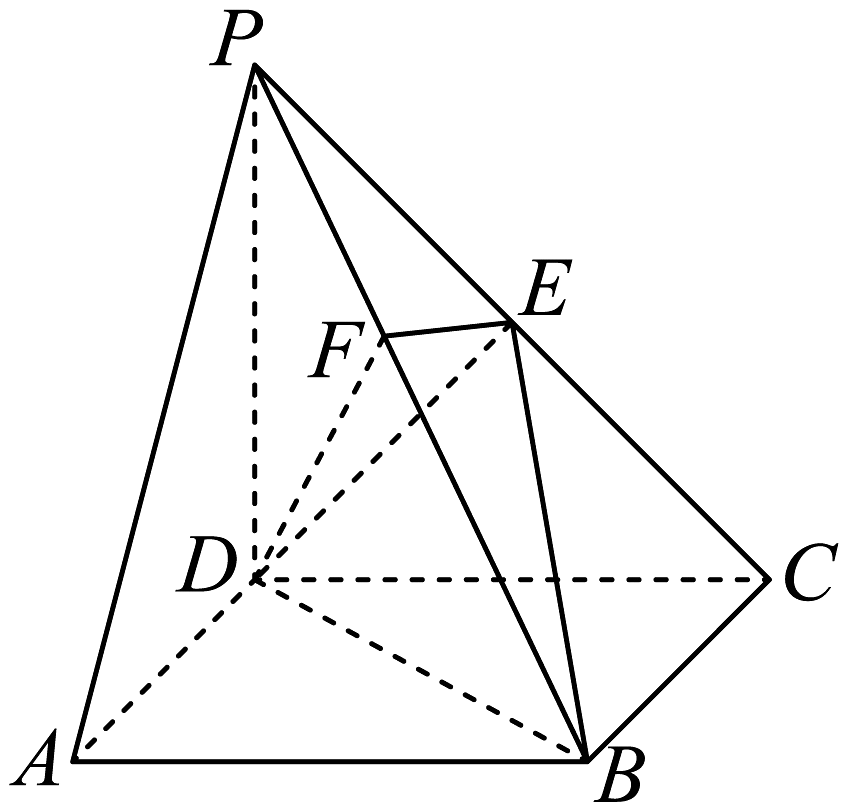 (1)、求证:面;(2)、求平面与平面的夹角的大小;(3)、求点到平面的距离.
(1)、求证:面;(2)、求平面与平面的夹角的大小;(3)、求点到平面的距离. -
9、若 , , , 则以下不等式正确的是( )A、 B、 C、 D、
-
10、已知函数 , .若的零点恰为的零点,则a的最大值是.
-
11、已知抛物线的焦点为F,斜率为1的直线l过F与C交于A,B两点,AB的中点到抛物线准线的距离为8,则 .
-
12、已知平面向量 , , 则( )A、当时, B、若 , 则 C、若 , 则 D、若与的夹角为钝角,则
-
13、在斜三角形中,角的对边分别为 , 点满足 , 且 , 则的面积为( )A、 B、 C、 D、
-
14、已知实数 , 设函数
(1)当时,求函数的单调区间;
(2)对任意均有 求的取值范围.
注:为自然对数的底数.
-
15、已知数列的前n项和满足 .(1)、写出数列的前三项;(2)、求数列的通项公式;(3)、证明:对任意的整数 , 有 .
-
16、已知椭圆:的两个焦点与短轴的一个端点是直角三角形的三个顶点,直线:与椭圆有且只有一个公共点T.
(Ⅰ)求椭圆的方程及点的坐标;
(Ⅱ)设是坐标原点,直线平行于 , 与椭圆交于不同的两点、 , 且与直线交于点 , 证明:存在常数 , 使得 , 并求的值.
-
17、水稻苗经过一个培育周期的生长株高达到8cm左右时最适宜播种,过高或过低都会影响后期的生产管理.根据长期的试验观察,在正常的培育环境下水稻苗经过一个培育周期生长的株高服从正态分布 , 并且符合原则.为了监控水稻苗的生长状况,检验员会从经过了一个培育周期的水稻苗中随机抽取20株,并测量其株高(单位:cm).(1)、把株高在之外的水稻苗称作异常苗,记表示异常苗的数量,求可能取值的个数、及.(2)、监控部门要求,如果在抽取的水稻苗中出现了异常苗,就认定这个培育周期的培育环境出现了异常情况,需要对培育环境进行检查和修正.
(ⅰ)监控部门的要求合理吗?请说明理由.
(ⅱ)下面是检验员从经过了一个培育周期的水稻苗中随机抽取的20株水稻苗的株高:
编号
1
2
3
4
5
6
7
8
9
10
株高/cm
7.98
8.01
8.00
8.03
7.99
7.83
7.99
8.28
7.05
7.69
编号
11
12
13
14
15
16
17
18
19
20
株商/cm
8.00
8.41
7.75
8.38
7.72
7.69
8.04
8.29
7.82
8.05
其中, 为抽取的第株水稻苗的株高,.请判断是否需对这个培育周期的培育环境进行检查和修正?若要修正,剔除异常苗的株高,求余下的数据估计和(精确到0.01).
附:若随机变量X服从正态分布 , 则 ,
-
18、如图,平面平面 , , 直线AM与直线PC所成的角为 , 又 .
 (1)、求证:;(2)、求二面角的大小;(3)、求多面体的体积.
(1)、求证:;(2)、求二面角的大小;(3)、求多面体的体积. -
19、已知 , 函数 , 若存在 , 使得 , 则实数的最大值是.
-
20、已知的展开式中各项系数的和是128,则展开式中的系数是 . (以数字作答)