相关试卷
- 高中数学人教新课标A版必修3 第一章 算法初步 1.3算法案例
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.3循环语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.1输入语句、输出语句和赋值语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.1算法与程序框图(包括1.1.1算法的概念,1.1.2程序框图与算法的基本逻辑结构)
- 高中数学人教新课标A版必修3 第三章 概率 3.3几何概型
- 高中数学人教新课标A版必修3 第三章 概率 3.2古典概型
- 高中数学人教新课标A版 必修3 第三章 概率 3.1.3概率的基本性质
- 高中数学人教新课标A版必修3 第三章 概率 3.1.1随机事件的概率,3.1.2概率的意义
- 高中数学人教新课标A版必修3 第二章 统计 2.3变量间的相关关系(包括2.3.1变量间的相关关系,2.3.2两个变量的线性相关)
- 高中数学人教新课标A版必修3 第二章 统计 2.2.2用样本的数字特征估计总体的数字特征
-
1、已知 , 分别为随机事件A,B的对立事件, , , 则( )A、 B、 C、若A,B独立,则 D、若A,B互斥,则
-
2、已知向量 , 若 , 则( )A、2 B、3 C、 D、
-
3、已知指数函数 .(1)、求的值;(2)、若 , 求的值;(3)、若 , 求的取值范围.
-
4、在平面直角坐标系中,已知直线与椭圆交于点A,B(A在x轴上方),且 . 设点A在x轴上的射影为N,三角形ABN的面积为2(如图1).
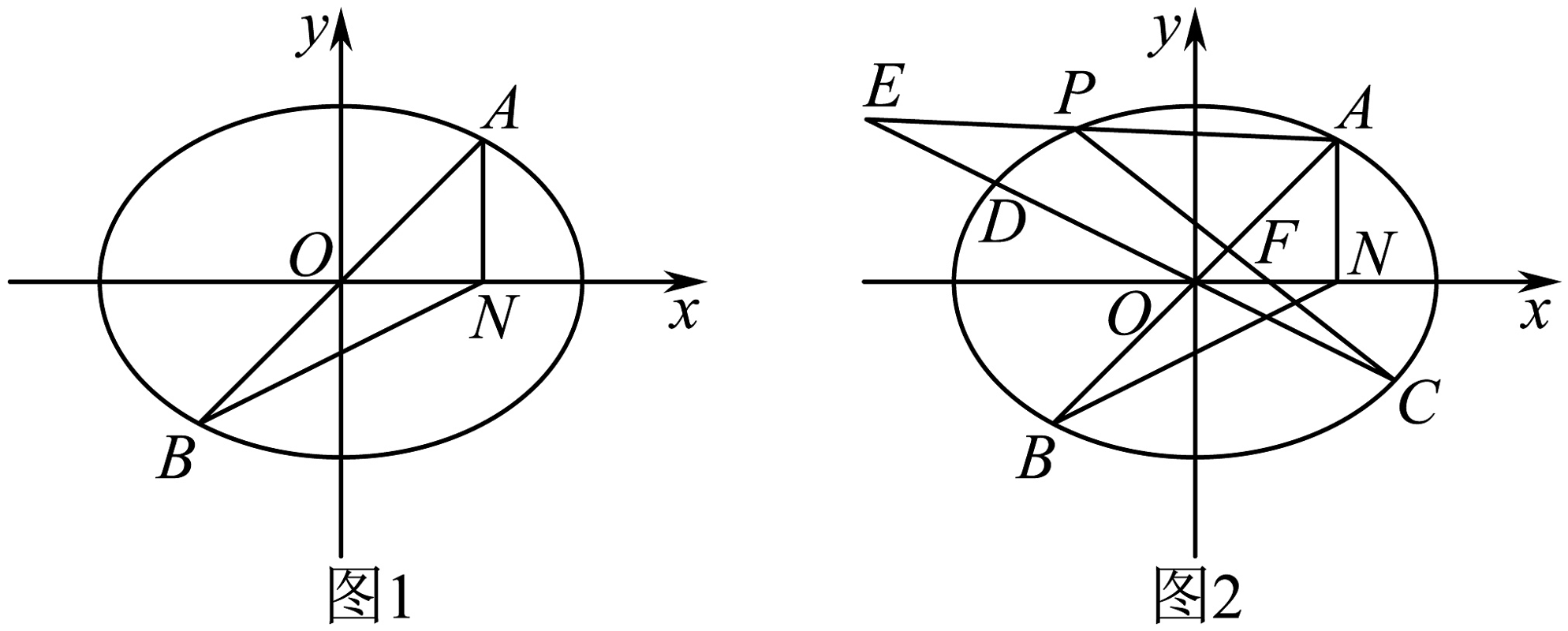
(1)求椭圆的方程;
(2)设平行于AB的直线与椭圆相交,其弦的中点为Q.
①求证:直线OQ的斜率为定值;
②设直线OQ与椭圆相交于两点C,D(D在x轴的上方),点P为椭圆上异于A,B,C,D一点,直线PA交CD于点E,PC交AB于点F,如图2,求证:为定值.
-
5、如图,在四棱锥中, , 四边形是菱形,是棱上的动点,且 .
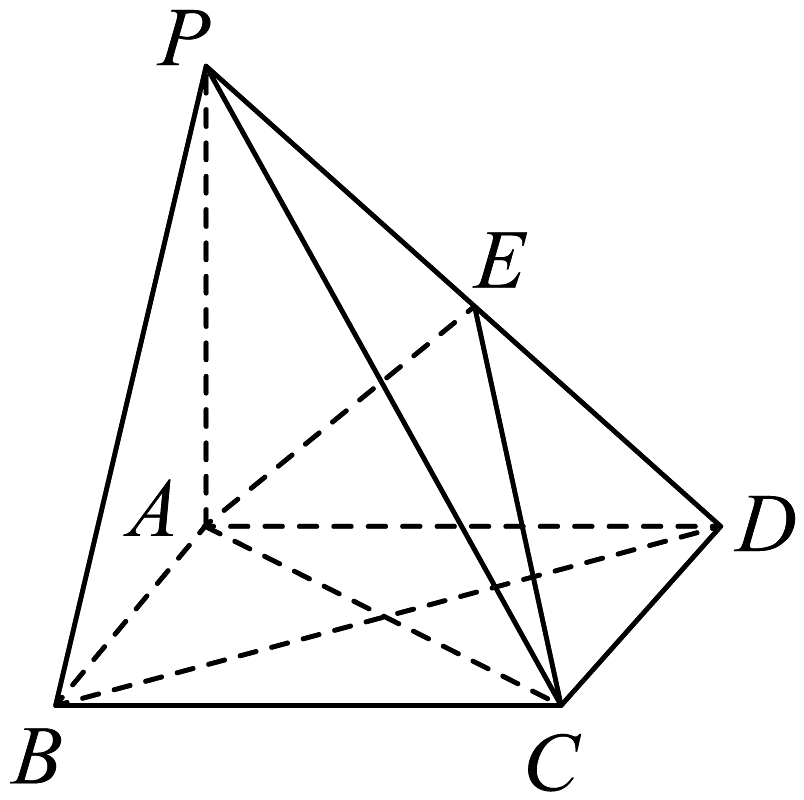 (1)、证明:平面 .(2)、是否存在实数 , 使得平面与平面所成锐二面角的余弦值是?若存在,求出的值;若不存在,请说明理由.
(1)、证明:平面 .(2)、是否存在实数 , 使得平面与平面所成锐二面角的余弦值是?若存在,求出的值;若不存在,请说明理由. -
6、会员足够多的某知名咖啡店,男会员占60%,女会员占40%.现对会员进行服务质量满意度调查.根据调查结果得知,男会员对服务质量满意的概率为 , 女会员对服务质量满意的概率为 .(1)、随机选取一名会员,求其对服务质量满意的概率;(2)、从会员中随机抽取3人,记抽取的3人中,对服务质量满意的人数为 , 求的分布列和数学期望.
-
7、若数列满足( , 为常数),则称数列为“调和数列”.已知数列为“调和数列”,下列说法正确的是( )A、若 , 则 B、若 , 且 , , 则 C、若中各项均为正数,则 D、若 , , 则
-
8、记表示 , 二者中较大的一个,函数 , , 若 , , 使得成立,则的取值范围是( )A、 B、 C、 D、
-
9、已知函数为偶函数,则不等式的解集为( )A、 B、 C、 D、
-
10、已知球的半径为1,其内接圆锥的高为 , 则该圆锥的侧面积为( )A、 B、 C、 D、
-
11、已知 , 则( )A、 B、 C、 D、
-
12、已知为虚数单位,若复数z满足 , 则( )A、1 B、 C、2 D、
-
13、若集合 , , 则( )A、 B、 C、 D、
-
14、已知函数.(1)、若时,求的单调区间;(2)、设函数在区间上的最小值为 , 求的表达式.
-
15、某汽车公司的研发部研制出一款新型的能源汽车并通过各项测试准备投入量产.生产该新能源汽车需年固定成本为50万元,每生产1辆汽车需投入16万元,该公司一年内共生产汽车辆,并全部销售完.每辆汽车的销售收入为(万元).(1)、求利润(万元)关于年产量(辆)的函数解析式.(2)、当年产量为多少辆时,该汽车公司所获得的利润最大?并求出最大利润.
-
16、已知函数 , 且满足 , .(1)、求和的值;(2)、判断在上的单调性,并用定义证明.
-
17、(1)计算;
(2)解不等式;
(3)已知 , 求的值.
-
18、已知函数 , 若存在 , 使得 , 则的取值范围是.
-
19、若 , , 则的取值范围.
-
20、对于定义域为R的函数 , 若存在非零实数 , 使得函数在和上与轴都有交点,则称为函数的一个“界点”,则下列函数中,存在界点的是( )A、 B、 C、 D、