相关试卷
- 高中数学人教新课标A版必修3 第一章 算法初步 1.3算法案例
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.3循环语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.1输入语句、输出语句和赋值语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.1算法与程序框图(包括1.1.1算法的概念,1.1.2程序框图与算法的基本逻辑结构)
- 高中数学人教新课标A版必修3 第三章 概率 3.3几何概型
- 高中数学人教新课标A版必修3 第三章 概率 3.2古典概型
- 高中数学人教新课标A版 必修3 第三章 概率 3.1.3概率的基本性质
- 高中数学人教新课标A版必修3 第三章 概率 3.1.1随机事件的概率,3.1.2概率的意义
- 高中数学人教新课标A版必修3 第二章 统计 2.3变量间的相关关系(包括2.3.1变量间的相关关系,2.3.2两个变量的线性相关)
- 高中数学人教新课标A版必修3 第二章 统计 2.2.2用样本的数字特征估计总体的数字特征
-
1、设集合 , , 则( )A、 B、 C、 D、
-
2、函数的定义域为 , 若存在正实数 , 对任意的 , 总有 , 则称函数具有性质.(1)、判断下列函数是否具有性质 , 并说明理由.
①;②;
(2)、已知为二次函数,若存在正实数 , 使得函数具有性质.用反证法证明:是偶函数;(3)、已知 , 为给定的正实数,若函数具有性质 , 求的取值范围.(用表示) -
3、已知函数 , 满足 .(1)、求函数图象的对称中心;(2)、当时,求的最小值;(3)、若对任意实数 , 恒成立,求实数的取值范围.
-
4、已知函数 .(1)、判断并证明的奇偶性;(2)、判断并证明的单调性;(3)、若对任意的 , 都有不等式恒成立,求实数的取值范围.
-
5、已知全集 , 不等式的解集是 , , .(1)、计算;(2)、若不等式的解集为 , 且“”是“”的充分不必要条件,求实数的取值范围.
-
6、(1);
(2)求的值.
-
7、已知函数 ,满足对任意的实数且 , 都有 , 则实数的取值范围是 .
-
8、幂函数在上单调递减,则m的值为 .
-
9、已知函数 , 若函数有四个零点,从小到大依次为 , , , , 则下列说法正确的是( )A、 B、的最小值为4 C、 D、方程最多有10个不同的实根
-
10、下列说法正确的有( )A、当时,的最大值是5 B、当时, C、已知正实数满足 , 则的最小值是2 D、的最小值为
-
11、下列函数中,既是偶函数,又在上单调递增的是( )A、 B、 C、 D、
-
12、已知函数的最小值为0,则( )A、 B、 C、 D、
-
13、中国茶文化源远流传,博大精深,茶水的口感与茶叶的类型和水的温度有关,某种绿茶用的水泡制,再等到茶水温度降至时饮用,可以产生最佳口感.为了控制水温,某研究小组联想到牛顿提出的物体在常温下的温度变化冷却规律:设物体的初始温度是 , 经过后的温度是 , 则 , 其中表示环境温度,表示半衰期.该研究小组经过测量得到,刚泡好的绿茶水温度是 , 放在的室温中,以后茶水的温度是 , 在上述条件下,大约需要放置多长时间能达到最佳饮用口感?(结果精确到0.1,参考数据 , )( )A、 B、 C、 D、
-
14、已知奇函数的定义域为 , 对任意的满足 , 且在区间上单调递增,若 , , , 则的大小关系为( )A、 B、 C、 D、
-
15、函数的图象大致为( )A、
 B、
B、 C、
C、 D、
D、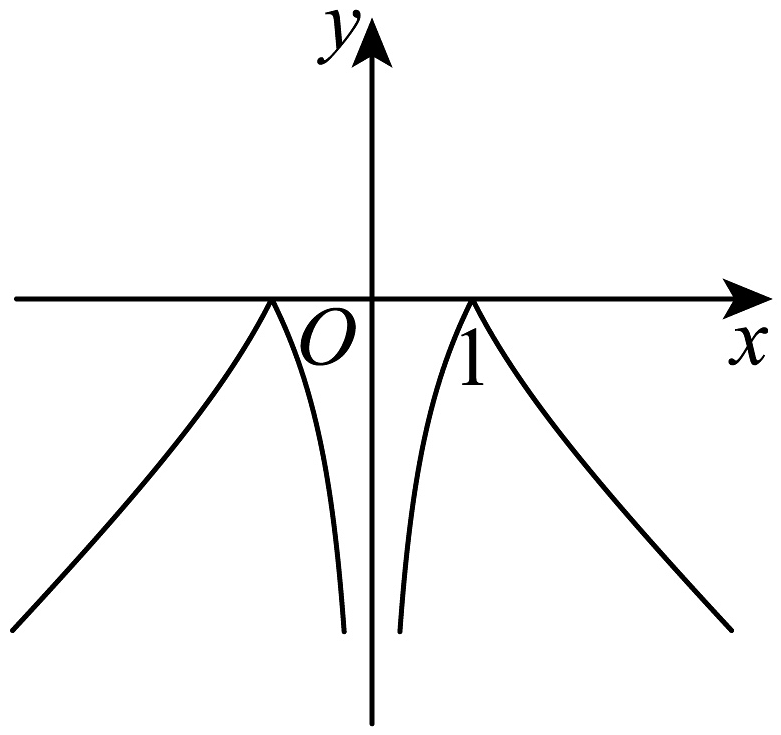
-
16、已知实数 ,则下列不等式一定成立的是( )A、 B、 C、 D、
-
17、已知命题 , , 则( ).A、 , B、 , C、 , D、 ,
-
18、已知 , 则( )A、 B、 C、 D、
-
19、已知 , 则 .
-
20、(1)若 , 求的值;
(2)化简求值:.