相关试卷
- 高中数学人教新课标A版必修3 第一章 算法初步 1.3算法案例
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.3循环语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.1输入语句、输出语句和赋值语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.1算法与程序框图(包括1.1.1算法的概念,1.1.2程序框图与算法的基本逻辑结构)
- 高中数学人教新课标A版必修3 第三章 概率 3.3几何概型
- 高中数学人教新课标A版必修3 第三章 概率 3.2古典概型
- 高中数学人教新课标A版 必修3 第三章 概率 3.1.3概率的基本性质
- 高中数学人教新课标A版必修3 第三章 概率 3.1.1随机事件的概率,3.1.2概率的意义
- 高中数学人教新课标A版必修3 第二章 统计 2.3变量间的相关关系(包括2.3.1变量间的相关关系,2.3.2两个变量的线性相关)
- 高中数学人教新课标A版必修3 第二章 统计 2.2.2用样本的数字特征估计总体的数字特征
-
1、函数的定义域是( )A、 B、 C、 D、
-
2、已知复数的实部和虚部分别为5和 , 则实数和的值分别是( )A、2, B、2,1 C、 , 2 D、1,
-
3、阅读下列材料,回答问题:
如图,在空间直角坐标系中,过原点与轴成角的直线绕轴一周,生成以为顶点轴为对称轴的两个圆锥形的几何体 , 不经过原点与轴成角的平面截几何体的表面得到的截口曲线称为圆锥曲线.

当时,平面截几何体的表面得到的截口曲线在一个圆锥上,以下证明它是椭圆:如图,在该圆锥内放置两球和 , 使它们都与圆锥相切(即与圆锥的每条母线相切,切点分别形成圆和圆)且与平面相切(位于平面上下两侧),切点分别为和 , 在截口曲线上任取一点P,作直线交圆于点 , 连接和 , 因为和都是大球的切线段,所以 , 同理 , 所以 , 因为两球外离,和分别是两球的内外公切线段,都为定值且 , 所以此时平面截圆锥得到的圆锥曲线满足椭圆定义,应为椭圆.依据上述材料所述,请回答:
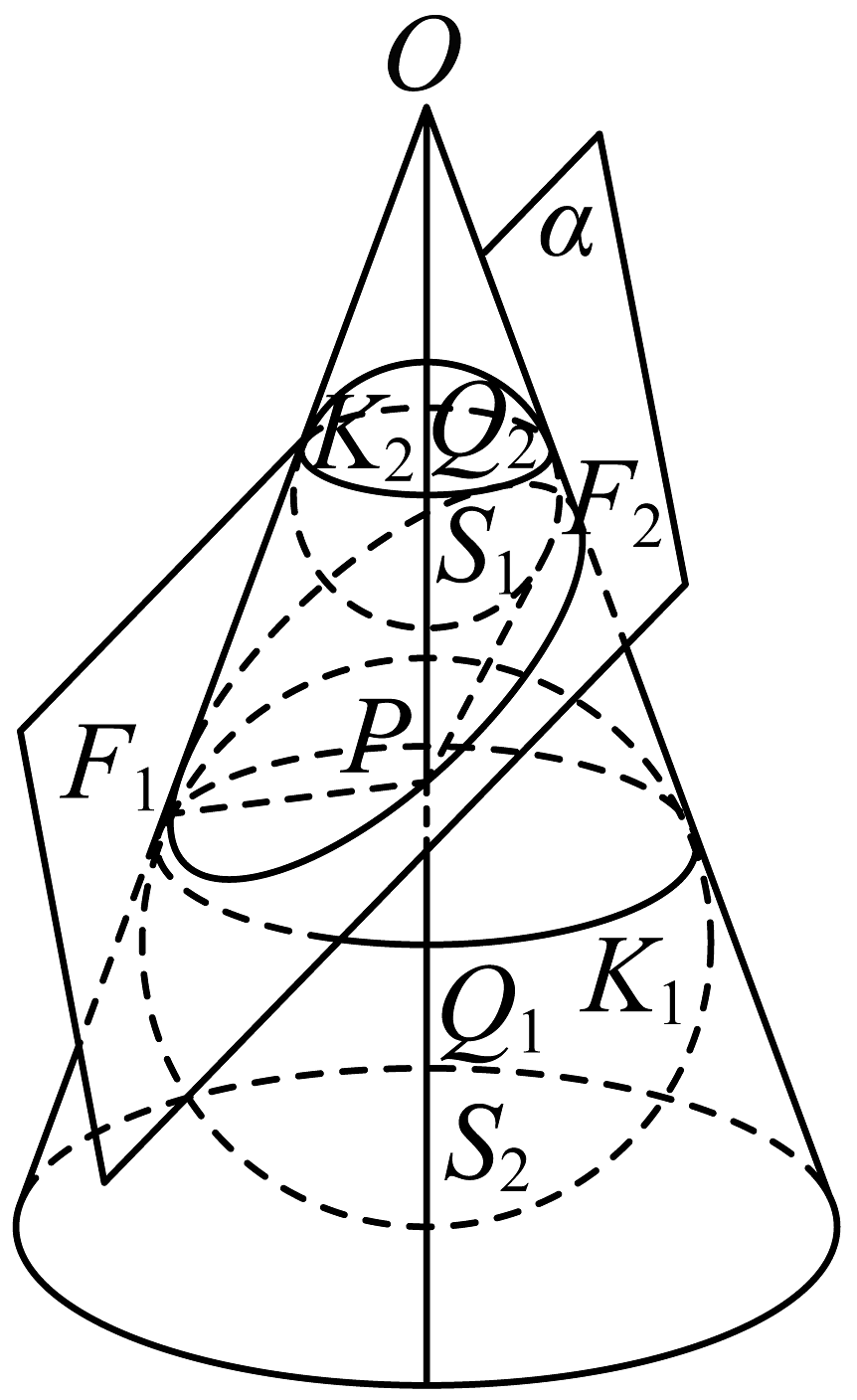 (1)、当时,对应的圆锥曲线是什么曲线?(直接回答不必证明)(2)、当 , 对应的圆锥曲线是什么曲线?并根据所给图形利用材料所提供的思路进行证明;
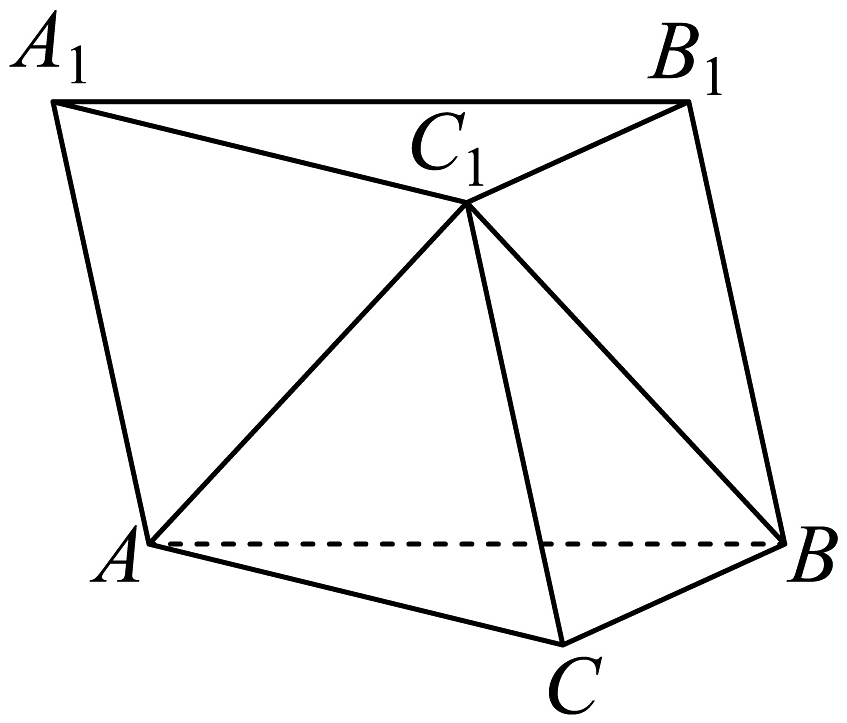
(1)、当时,对应的圆锥曲线是什么曲线?(直接回答不必证明)(2)、当 , 对应的圆锥曲线是什么曲线?并根据所给图形利用材料所提供的思路进行证明; (3)、如图,将等边绕边旋转至 , 并且使二面角为直二面角,动点在平面上并且 , 判断动点的轨迹,并求其离心率.
(3)、如图,将等边绕边旋转至 , 并且使二面角为直二面角,动点在平面上并且 , 判断动点的轨迹,并求其离心率.
-
4、已知椭圆 , 过点 , 离心率为 , 过点的直线交椭圆于两点,若直线的斜率都存在且分别为 ,(1)、求椭圆的方程(2)、求的值
-
5、如图,为圆柱的轴截面,为底面半圆周上一点,为中点,
 (1)、若 , 求的长(2)、若 , 求平面与平面所成夹角的余弦值
(1)、若 , 求的长(2)、若 , 求平面与平面所成夹角的余弦值 -
6、已知圆C: .(1)、若直线l过点且被圆C截得的弦长为2,求直线l的方程;(2)、从圆C外一点P向圆C引一条切线,切点为M,O为坐标原点,且 , 求的最小值.
-
7、如图,已知是相互垂直的两条异面直线,直线与相交且垂直,垂足为 , 且线段 , 动点分别位于直线上,若直线与所成的角 , 线段的中点为 , 则以下结论:

①的长度为定值4.
②三棱锥的体积为定值.
③点的轨迹是圆;
其中正确的有(填写编号)
-
8、在平面直角坐标系中,已知某直线沿轴正方向平移3个单位,再沿轴负方向平移2个单位直线回到原来位置,则此直线的斜率.
-
9、已知四边形的四个顶点都在椭圆上,对角线过原点 , 且 , 则( )A、是定值 B、是定值 C、四边形的面积是定值 D、四边形的周长是定值
-
10、在空间直角坐标系中,已知点 , 为的重心,则( )A、点的坐标是 B、是平面的法向量 C、平面过原点 D、为锐角三角形
-
11、已知抛物线 , 焦点为 , 准线为 , 弦过点,则下列说法正确的是( )A、焦点的坐标为 B、准线的方程为 C、若 , 则 D、弦的长度
-
12、已知动直线 , 圆 , 则直线与圆的位置关系是( )A、相交 B、相切 C、相离 D、与值有关,无法确定
-
13、已知直线在轴上的截距是 , 在轴上的截距是3,则直线的方程是( )A、 B、 C、 D、
-
14、已知函数.(1)、若函数在定义域上单调递增,求的取值范围;(2)、若;求证:;(3)、设 , 是函数的两个极值点,求证:.
-
15、已知集合.(1)、集合 , 且中的任意三个不同的元素 , , 都有.
(i)当时,写出一个满足条件的恰有四个元素的集合;
(ii)对于任意给定的 , 求集合中的元素个数的最大值.
(2)、已知集合P={C|CA}, , 且同时满足以下条件:① , , 都有(其中 , , );② , , 使得(其中).求集合中的元素个数. -
16、如图,在三棱柱中,平面平面 , 平面.
 (1)、求证:;(2)、若二面角的正弦值为 , 且 , 求.
(1)、求证:;(2)、若二面角的正弦值为 , 且 , 求. -
17、如图所示的五面体为《九章算术》中记载的羡除,它指的是墓道或隧道.其中 , 四边形 , , 均为等腰梯形,平面平面 , , , , 和间的距离为2,和间的距离为4,则该羡除的体积为.

-
18、已知椭圆和双曲线的焦点相同,则.
-
19、已知函数 , 则( )A、 B、当时, C、当时, D、当时,
-
20、已知 , , , , 其中 , 点为平面内一点,记点到 , 的距离分别为 , , 则下列条件中能使点的轨迹为椭圆的是( )A、 B、 C、 D、