相关试卷
- 高中数学人教新课标A版必修3 第一章 算法初步 1.3算法案例
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.3循环语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.1输入语句、输出语句和赋值语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.1算法与程序框图(包括1.1.1算法的概念,1.1.2程序框图与算法的基本逻辑结构)
- 高中数学人教新课标A版必修3 第三章 概率 3.3几何概型
- 高中数学人教新课标A版必修3 第三章 概率 3.2古典概型
- 高中数学人教新课标A版 必修3 第三章 概率 3.1.3概率的基本性质
- 高中数学人教新课标A版必修3 第三章 概率 3.1.1随机事件的概率,3.1.2概率的意义
- 高中数学人教新课标A版必修3 第二章 统计 2.3变量间的相关关系(包括2.3.1变量间的相关关系,2.3.2两个变量的线性相关)
- 高中数学人教新课标A版必修3 第二章 统计 2.2.2用样本的数字特征估计总体的数字特征
-
1、下列说法中正确的是( )A、若复数 , 则复数在复平面内对应的点位于第一象限 B、已知复数z满足 , 则 C、是关于x的方程(m,n为实数)在复数集内的一个根,则实数n的值为26 D、若复数z满足若 , 且 , 则的最小值为4
-
2、将个互不相等的数排成下表:

记 , , 则下列判断中,一定不成立的是( )
(注:分别表示集合最大值和最小值.)
A、 B、 C、 D、 -
3、分形几何学是数学家伯努瓦·曼德尔布罗特在世纪年代创立的一门新的数学学科,它的创立为解决众多传统科学领域的难题提供了全新的思路.按照如图1所示的分形规律可得如图2所示的一个树形图.若记图2中第行黑圈的个数为 , 则( )
 A、4 B、6 C、8 D、10
A、4 B、6 C、8 D、10 -
4、已知 , 若 , 则实数=( )A、﹣4 B、1 C、2 D、6
-
5、已知函数的部分图象如图所示,若将函数的图象向右平移个单位后所得曲线关于轴对称,则的最小值为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
6、已知是定义在上的偶函数,且 , 恒成立,若 , 则满足的实数的取值范围是.
-
7、对于定义域为的函数 , 如果存在区间 , 同时满足:①在上是单调函数;②当时, , 则称是该函数的“优美区间”.(1)、求证:是函数的一个“优美区间”;(2)、求证:函数不存在“优美区间”;(3)、已知函数有“优美区间” , 当取得最大值时求的值.
-
8、文明城市是反映城市整体文明水平的综合性荣誉称号.作为普通市民,既是文明城市的最大受益者,又是文明城市的主要创造者.六盘水市为提高市民对文明城市创建的认识,举办了“创建文明城市”知识竞赛(满分100分),从所有答卷的成绩中抽取了容量为100的样本,将样本(成绩均为不低于50分的整数)分成五段:得到如图所示的频率分布直方图.
 (1)、求频率分布直方图中的值和估计样本的下四分位数;(2)、按照分层抽样的方法,从样本中抽取20份成绩,应从中抽取多少份;(3)、已知落在的平均成绩是53,方差是4;落在的平均成绩为65,方差是7,求成绩落在的平均数和方差.
(1)、求频率分布直方图中的值和估计样本的下四分位数;(2)、按照分层抽样的方法,从样本中抽取20份成绩,应从中抽取多少份;(3)、已知落在的平均成绩是53,方差是4;落在的平均成绩为65,方差是7,求成绩落在的平均数和方差.(注:若将总体划分为若干层,随机抽取两层,通过分层随机抽样,每层抽取的样本量、样本平均数和样本方差分别为:.记这两层总的样本平均数为 , 样本方差为 , 则)
-
9、如图,直三棱柱中,分别是的中点,.
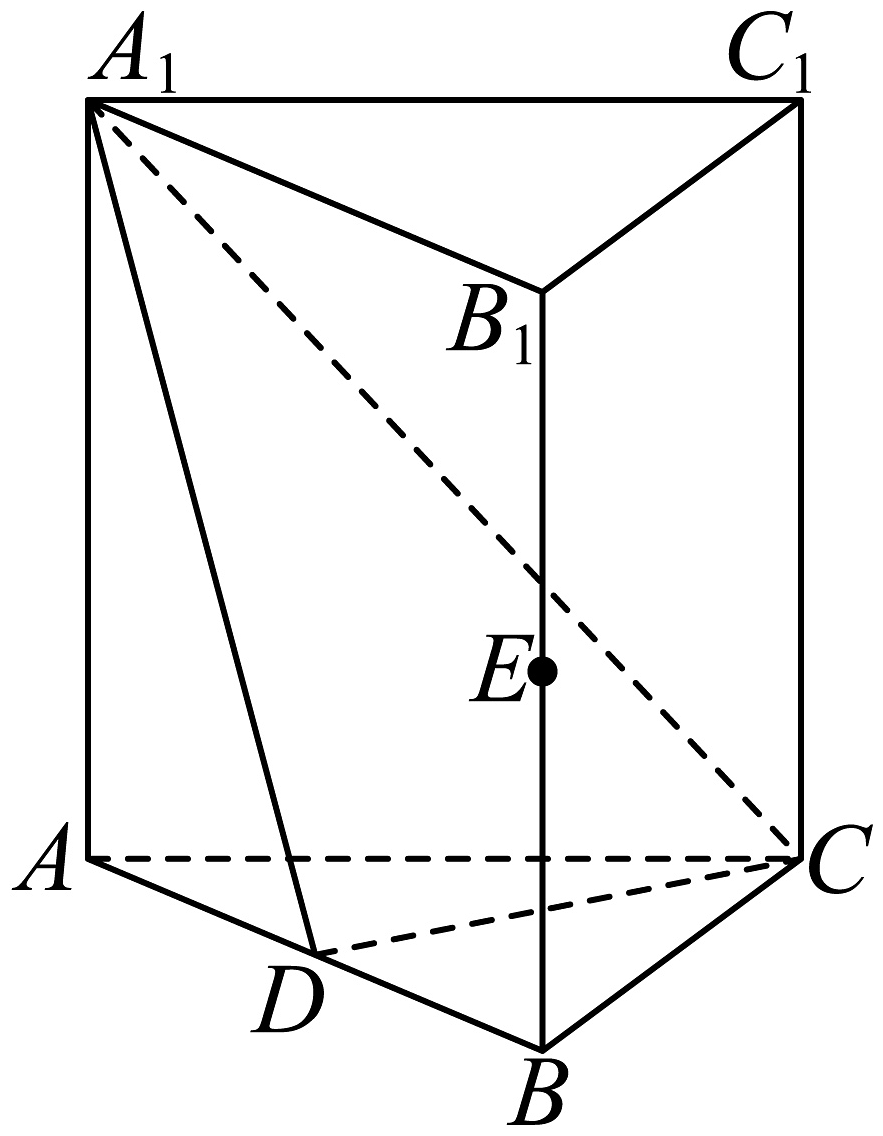 (1)、证明:平面;(2)、求直线与平面所成角的正弦值.
(1)、证明:平面;(2)、求直线与平面所成角的正弦值. -
10、已知函数 ,(1)、求函数的最小正周期;(2)、将函数图象上所有点的横坐标伸长到原来的2倍,纵坐标不变;再向左平移个单位长度,得到函数的图象.当时,求函数的最值.
-
11、已知二次函数的图象经过点且对称轴为.(1)、求的解析式;(2)、求不等式的解集.
-
12、已知分别为三个内角的对边,且 , 则面积的最大值是.
-
13、已知函数 , 则.
-
14、已知 , 则.
-
15、已知向量的数量积(又称向量的点积或内积): , 其中表示向量的夹角;定义向量的向量积(又称向量的叉积或外积): , 其中表示向量的夹角,则下列说法正确的是( )A、的面积为 B、若为非零向量,且 , 则 C、若 , 则的最小值为 D、已知点为坐标原点,则
-
16、下列选项正确的是( )A、 B、 C、 D、
-
17、如图在正方体中,分别是的中点,则下列选项正确的是( )
 A、平面 B、平面 C、四点共面 D、与所成的角为
A、平面 B、平面 C、四点共面 D、与所成的角为 -
18、已知 , 则的值为( )A、 B、 C、 D、
-
19、已知函数是定义域为的奇函数,.当时, , 则( )A、-2 B、-1 C、0 D、2
-
20、在中,是边上靠近点的三等分点,是的中点,若 , 则( )A、0 B、 C、 D、1