相关试卷
- 高中数学人教新课标A版必修3 第一章 算法初步 1.3算法案例
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.3循环语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.1输入语句、输出语句和赋值语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.1算法与程序框图(包括1.1.1算法的概念,1.1.2程序框图与算法的基本逻辑结构)
- 高中数学人教新课标A版必修3 第三章 概率 3.3几何概型
- 高中数学人教新课标A版必修3 第三章 概率 3.2古典概型
- 高中数学人教新课标A版 必修3 第三章 概率 3.1.3概率的基本性质
- 高中数学人教新课标A版必修3 第三章 概率 3.1.1随机事件的概率,3.1.2概率的意义
- 高中数学人教新课标A版必修3 第二章 统计 2.3变量间的相关关系(包括2.3.1变量间的相关关系,2.3.2两个变量的线性相关)
- 高中数学人教新课标A版必修3 第二章 统计 2.2.2用样本的数字特征估计总体的数字特征
-
1、在复平面内,对应的点位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限
-
2、已知双曲线 , 左、右顶点分别为 , 过点的直线交双曲线于两点.(1)、若的离心率为2,求.(2)、若为等腰三角形,且点在第一象限,求点的坐标.(3)、连接(为坐标原点)并延长交于点 , 若 , 求的最大值.
-
3、已知k、 , 函数的定义域为 , 直线l的方程为 , 记集合 .(1)、若 , 求集合;(2)、若 , 且存在实数k、m使得集合中有且只有两个元素,求实数b的取值范围;(3)、若函数的图象是一条连续曲线,且其导函数是定义域为的严格减函数,求证:“集合是单元素集合”是“直线l是曲线在点处的切线”的充要条件.
-
4、如图,在三棱锥P⁃ABC中,平面PAB⊥平面PAC,BC=2AB=2,∠ABC=.
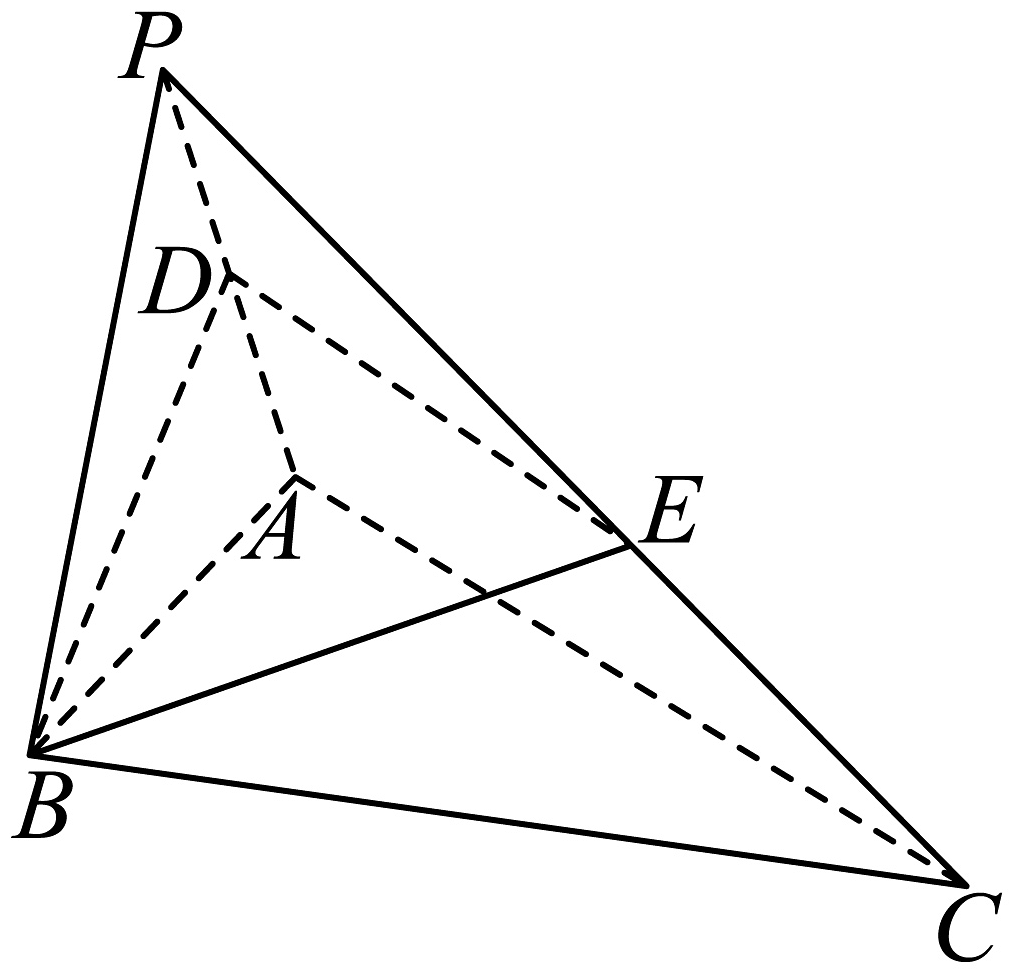 (1)、证明:PB⊥AC;(2)、若侧面PAB是等边三角形,点D满足=λ(0<λ<1),过B,D两点作平面α,满足直线AC∥α,设平面α与PC交于点E,直线PC与平面α所成的角为 , 求λ的值.
(1)、证明:PB⊥AC;(2)、若侧面PAB是等边三角形,点D满足=λ(0<λ<1),过B,D两点作平面α,满足直线AC∥α,设平面α与PC交于点E,直线PC与平面α所成的角为 , 求λ的值. -
5、某绿色水果生态园在某种水果收获的.随机摘下该水果100个作为样本,其质量分别在 , , , , , (单位:克)中,经统计,样本的频率分布直方图如图所示:
 (1)、求图中a的值;(2)、现按分层抽样的方法从质量为 , 的水果中随机抽取6个,再从6个中随机抽取3个,求这3个水果中恰有1个质量在内的概率;(3)、某经销商来收购水果时,该生态园有水果约10000个要出售.
(1)、求图中a的值;(2)、现按分层抽样的方法从质量为 , 的水果中随机抽取6个,再从6个中随机抽取3个,求这3个水果中恰有1个质量在内的概率;(3)、某经销商来收购水果时,该生态园有水果约10000个要出售.经销商提出如下两种收购方案:
方案A:所有水果以10元/千克收购;
方案B:对质量低于250克的水果以2元/个收购,不低于250克的以3元/个收购.假设同组中的每个数据都用该组区间的中点值代替,请估算该生态园选择哪种方案获利更多?
-
6、折纸是一项玩法多样的活动.通过折叠纸张,可以创造出各种各样的形状和模型,如动物、花卉、船只等.折纸不仅是一种艺术形式,还蕴含了丰富的数学知识.在纸片中, , , 所对的边分别为 , , , 的面积为 , .(1)、证明:;(2)、若 , 求的值;(3)、在(2)的条件下,若 , 是的中点,现需要对纸片做一次折叠,使点与点重合,求折叠后纸片重叠部分的面积.
-
7、若正整数m,n的公约数只有1,则称m,n互质.对于正整数是小于或等于n的正整数中与n互质的数的个数.函数以其首名研究者欧拉的名字命名,称为欧拉函数,例如 , 则.若数列的前n项和为 , 则.
-
8、已知 , 则.
-
9、函数的极值点为.
-
10、某校篮球社团准备招收新成员,要求通过考核才能加入,考核规则如下:报名参加该社团的学生投篮次,若投中次数不低于投篮次数的 , 则通过考核.学生甲准备参加该社团,且他的投篮命中率为0.9,每次是否投中相互独立.若 , 记甲通过考核的概率为 , 若 , 记甲通过考核的概率为 , 若 , 记甲通过考核的概率为 , 若 , 记甲通过考核的概率为 , 若 , 记甲通过考核的概率为 , 则( )A、 B、 C、 D、
-
11、已知各项均不为零的数列 , 其前项和是 , 且. 下列说法正确的是( )A、 B、若为递增数列,则的取值范围是 C、存在实数 , 使得为等比数列 D、 , 使得当时,总有
-
12、已知函数 , 则( )A、的图象关于直线对称 B、为了得到函数的图象,可将的图象向右平移个单位长度 C、在上的值域为 D、两个相邻的零点之差的绝对值为
-
13、在数列中, , , , 前项和为 , 则下列说法中不正确的是( )A、 B、 C、 D、
-
14、已知定义域为的函数满足 , 且 , 则不等式的解集是( )A、 B、 C、 D、
-
15、已知椭圆的短轴长为4,上顶点为 B ,O为坐标原点,点D为OB的中点,曲线的左、右焦点分别与椭圆 C 的左、右顶点重合,点P是双曲线E与椭圆C在第一象限的交点,且三点共线,直线的斜率 , 则双曲线E的实轴长为( )A、 B、 C、 D、
-
16、如图,在正方体中, , , 分别是棱 , 的中点,则正方体被平面所截得的截面周长是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
17、已知直线:与圆:交于 , 两点,则( )A、 B、4 C、 D、2
-
18、已知单调递减的等比数列满足 , 则( )A、 B、 C、512 D、1024
-
19、若( , 是虚数单位),则的值分别等于( )A、 B、 C、 D、
-
20、集合 , , 则( )A、 B、 C、 D、