相关试卷
- 高中数学人教新课标A版必修3 第一章 算法初步 1.3算法案例
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.3循环语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.1输入语句、输出语句和赋值语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.1算法与程序框图(包括1.1.1算法的概念,1.1.2程序框图与算法的基本逻辑结构)
- 高中数学人教新课标A版必修3 第三章 概率 3.3几何概型
- 高中数学人教新课标A版必修3 第三章 概率 3.2古典概型
- 高中数学人教新课标A版 必修3 第三章 概率 3.1.3概率的基本性质
- 高中数学人教新课标A版必修3 第三章 概率 3.1.1随机事件的概率,3.1.2概率的意义
- 高中数学人教新课标A版必修3 第二章 统计 2.3变量间的相关关系(包括2.3.1变量间的相关关系,2.3.2两个变量的线性相关)
- 高中数学人教新课标A版必修3 第二章 统计 2.2.2用样本的数字特征估计总体的数字特征
-
1、已知圆:与圆:有两条公切线,则实数的取值范围( )A、 B、 C、 D、
-
2、如图,在三棱锥中,已知是上靠近的三等分点,是的中点,则( )
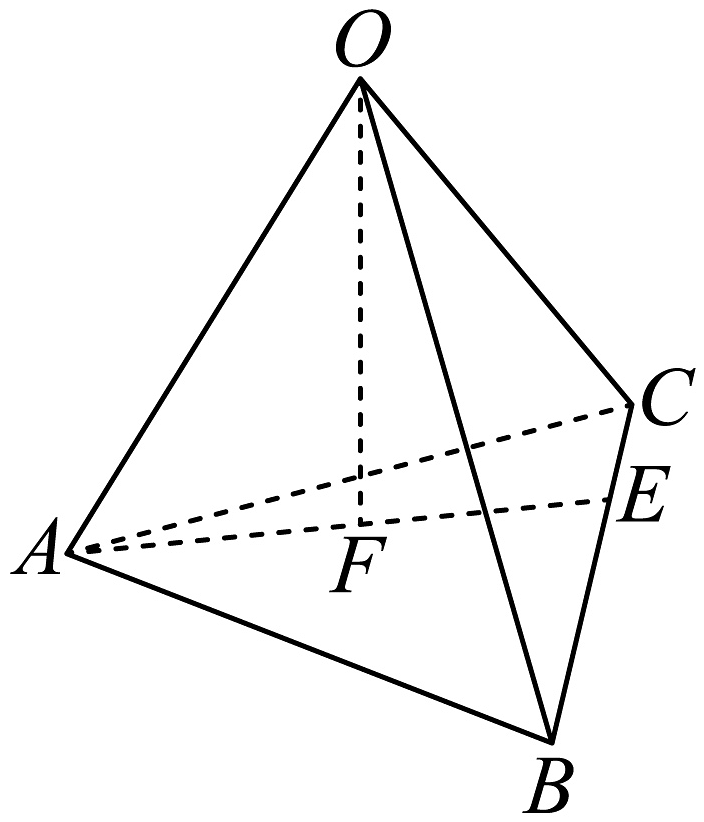 A、 B、 C、 D、
A、 B、 C、 D、 -
3、经过点作圆的切线,则切线方程为( )A、 B、 C、 D、
-
4、已知 , 分别为椭圆的左右焦点,为椭圆上一点,若 , 则为( )A、1 B、4 C、6 D、7
-
5、已知直线:与: , 若 , 则为( )A、 B、0 C、 D、
-
6、已知直线过、两点,则该直线的斜率为( )A、 B、 C、 D、
-
7、已知数列的前项和为 , , 且为与的等差中项,当时,总有.(1)、求数列的通项公式;(2)、记为在区间内的个数,记数列的前项和为 , 求.
-
8、已知数列满足 , , .
(1)若.
①求数列的通项公式;
②证明:对 , .
(2)若 , 且对 , 有 , 证明:.
-
9、济南新旧动能转换先行区,承载着济南从“大明湖时代”迈向“黄河时代”的梦想,肩负着山东省新旧动能转换先行先试的重任,是全国新旧动能转换的先行区.先行区将以“结构优化、质量提升”为目标,通过开放平台汇聚创新要素,坚持绿色循环保障持续发展,建设现代绿色智慧新城.2019年某智能机器人制造企业有意落户先行区,对市场进行了可行性分析,如果全年固定成本共需2000(万元),每年生产机器人(百个),需另投入成本(万元),且 , 由市场调研知,每个机器人售价6万元,且全年生产的机器人当年能全部销售完.
(1)求年利润(万元)关于年产量(百个)的函数关系式;(利润=销售额-成本)
(2)该企业决定:当企业年最大利润超过2000(万元)时,才选择落户新旧动能转换先行区.请问该企业能否落户先行区,并说明理由.
-
10、已知函数 , .
(Ⅰ)函数 , 分析在上的单调性.
(Ⅱ)若函数.
(i)当时,求的最小值;
(ii)当时,求零点的个数.
-
11、已知 , 求:(1)、的值.(2)、的值.
-
12、已知一个圆柱的轴截面是周长为12米的长方形,则满足这个条件的圆柱的最大体积是立方米.

-
13、已知数列满足 , , 则 .
-
14、函数的图象的一个对称中心的坐标是.
-
15、下列函数,最小正周期为的偶函数有( )A、 B、 C、 D、
-
16、已知函数 , 若 , 则实数的取值范围是( )A、 B、 C、 D、
-
17、已知 , , , 则A、 B、 C、 D、
-
18、为了得到函数
 的图象,只需把函数的图象上所有的点 A、向左平行移动个单位长度 B、向右平行移动个单位长度 C、向左平行移动个单位长度 D、向右平行移动个单位长度
的图象,只需把函数的图象上所有的点 A、向左平行移动个单位长度 B、向右平行移动个单位长度 C、向左平行移动个单位长度 D、向右平行移动个单位长度 -
19、对于数集M,定义M的特征函数: , 对于两个数集 , 定义.(1)、已知集合 ,
(i)求的值,并用列举法表示;
(ii)若用表示有限集合M所包含的元素个数,已知集合X是正整数集的子集,求的最小值(无需证明);
(2)、证明:. -
20、已知是定义在上的函数,若满足且.(1)、求的解析式;(2)、判断的单调性,并利用定义证明你的结论;(3)、设函数 , 若对都有成立,求的取值范围.