-
1、在数轴上，点A表示7，点B表示5，点O表示0，C为线段OB上一点，当以OC，CB，BA三条线段为边，可以围成等腰三角形时，点C表示什么数?
-
2、如图所示，在△ABC中，AD⊥BC，CE⊥AB，垂足分别为点D和点E，AD与CE交于点O，连结BO并延长交AC于点F，若AB=5，BC=4，AC=6，则CE∶AD∶BF值为.
-
3、如图所示为小明画的图形，每个正六边形的边长都相等，相邻两正六边形的边重合，点A，B，C均为正六边形的顶点，AB与地面BC所成的锐角为β.则tanβ的值为.
-
4、如图所示，在Rt△ABC中，AB=AC，∠A=90°，BD是角平分线，DE⊥BC，垂足为点E.若CD=5 ， 则AD的长是.
-
5、若等边三角形的重心到顶点的距离为2，则该等边三角形的边长为
-
6、如图所示，在等腰△ABC中，AB=AC，点D在BC边上，连结AD，且CD=5，AD=13，直线EF是腰AC的垂直平分线，若点M在EF上运动，则△CDM周长的最小值为.
-
7、若锐角满足且 ， 则的取值范围是.
-
8、如图所示，直线交x轴于A点，将一块等腰直角三角形纸板的直角顶点置于原点O，另两个顶点M，N恰落在直线上，若N点在第二象限内，则的值为（ ）
A、 B、 C、 D、 -
9、如图所示，等边△ABC和等边△CDE，其中B，C，E三点共线，连结AE，BD，CF，GH，有下列说法：①FC平分∠BFE；②GH∥BE；③S△ACH=S△BCG；④S△AHD=S△CHE.其中正确的有（ ）
A、1个 B、2个 C、3个 D、4个 -
10、如图所示，已知△ABC≌△A'BC'，AA'∥BC，∠ABC=70°，则∠CBC'的度数是（ ）
A、40° B、35° C、55° D、20° -
11、如图所示，已知D，E分别为△ABC的边AC，BC的中点，AF为△ABD的中线，连接EF，若四边形AFEC的面积为15，且AB=8，则△ABC中AB边上高的长为（ ）
A、3 B、6 C、9 D、无法确定 -
12、如图所示，在中， ， ， ， 则AB的长是（ ）
A、4 B、 C、5 D、 -
13、如图所示，已知在△ABC中，AB=6，AC=9，AD⊥BC于点D，M为AD上任一点，则MC2-MB2等于（ ）
A、9 B、35 C、45 D、无法计算 -
14、在△ABC中，若∠A∶∠B∶∠C=2∶3∶5，则△ABC是（ ）A、锐角三角形 B、直角三角形 C、钝角三角形 D、等腰三角形
-
15、如图所示，已知△ABC≌△DEF，点E，C，F，B在同一条直线上.下列结论中，正确的是（ ）
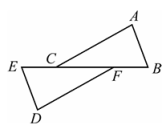A、∠B=∠D B、∠ACB=∠DEF C、AC=EF D、BF=CE -
16、如图所示，已知△ABC≌△DEF，DF和AC，EF和BC为对应边，若∠A=123°，∠F=39°，则∠DEF的度数为（ ）
A、18° B、20° C、39° D、123° -
17、如图所示，直线 ， 点C，A分别在 ， 上，以点C为圆心，CA长为半径画弧，交于点B，连结AB.若 ， 则的度数为（ ）
A、 B、 C、 D、 -
18、已知四边形ABCD内接于 ， 对角线AC与BD交于点E.
(1)、如图1，若AC为直径，点B是中点， ， .①求证：；
②求DC的长；
(2)、如图2，若 ， ， 且AC、BD不过点O，P、Q分别为AB、CD的中点，连结PE、EQ、QO、OP，试猜想四边形PEQO的形状，并证明你的猜想. -
19、已知二次函数.(1)、若二次函数经过点 ，
①求二次函数解析式；
②当时，求y的取值范围；
(2)、若 ， 点、、在二次函数图象上，请比较 ， ， 的大小. -
20、某工厂员工生产一款零件，员工的日工资结算方案如下：
方案一：基本工资每天20元，每生产一个零件加计2元，
方案二：当生产数量不超过100个时，发基本工资每天100元，每超过一个加计4元.
如图所示是日工资y（元）关于生产数量х（个）的函数图象，
(1)、求x>100时，方案二的日工资y（元）关于生产数量х（个）的函数表达式；(2)、甲员工发现他选择方案一所得的工资比选择方案二所得的工资高，求甲员工生产的零件个数的范围；(3)、乙员工发现他选择方案一所得的工资比选择方案二所得的工资少20元，则乙员工生产了多少个零件？