相关试卷

1、一枚质地均匀的正方体骰子（六个面分别标有数字1，2，3，4，5，6），投掷5次，分别记录每次骰子向上的一面出现的数字.根据下面的统计结果，能判断记录的这五个数字中一定没有出现数字6的是（）

A、中位数是3，众数是2 B、平均数是3，中位数是2 C、平均数是3，方差是2 D、平均数是3，众数是2

查看解析
2、如图所示的电路中，当随机闭合开关 $S_{1}$ ， $S_{2}$ ， $S_{3}$ 的两个时，灯泡能发光的概率为（）

A、 $\frac{2}{3}$ B、 $\frac{1}{2}$ C、 $\frac{1}{3}$ D、 $\frac{1}{6}$

查看解析
3、据统计，数学家群体是一个长寿群体，某研究小组随机抽取了收录约2200位数学家的《数学家传略辞典》中部分90岁及以上的长寿数学家的年龄为样本，对数据进行整理与分析，得到的统计图表（部分数据）如下，下列结论中，错误的是（）
年龄范围（岁）
人数（人）
90~91
25
92~93

94~95

96~97
11
98~99
10
100~101
m

A、该小组共统计了100名数学家的寿命 B、统计表中m的值为5 C、长寿数学家寿命在92~93岁的人数最多 D、《数学家传略辞典》中收录的寿命在96~97岁的数学家估计有110人

查看解析
4、如图所示，小球从A入口往下落，在每个交叉口都有向左下或向右下两种可能，且可能性相等，则小球从E出口落出的概率是（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{1}{4}$ D、 $\frac{1}{6}$

查看解析
5、豫剧是国家级非物质文化遗产，因其雅俗共赏，深受大众喜爱.正面印有豫剧经典剧目人物的三张卡片，它们除正面外完全相同.把这三张卡片背面朝上洗匀，从中随机抽取一张，放回洗匀后，再从中随机抽取一张，两次抽取的卡片正面相同的概率为（）

A、 $\frac{1}{9}$ B、 $\frac{1}{6}$ C、 $\frac{1}{5}$ D、 $\frac{1}{3}$

查看解析
6、为了解某市参加中考的32000名学生的体重情况，抽查了其中1600名学生的体重进行统计分析.下列叙述中，正确的是（）

A、32000名学生是总体 B、1600名学生的体重是总体的一个样本 C、每名学生是总体的一个个体 D、1600名学生是样本容量

查看解析
7、为发展学生的阅读素养，某校开设了《西游记》《三国演义》《水浒传》和《红楼梦》这四本书的整本书阅读项目，甲、乙两名同学都通过抽签的方式从这四个阅读项目中随机抽取1个，则他们恰好抽到同一个阅读项目的概率是（）

A、 $\frac{1}{16}$ B、 $\frac{1}{12}$ C、 $\frac{1}{6}$ D、 $\frac{1}{4}$

查看解析
8、下列说法中，正确的是（）

A、任意掷一枚质地均匀的骰子，掷出的点数一定是奇数 B、“从一副扑克牌中任意抽取一张，抽到大王”是必然事件 C、了解一批冰箱的使用寿命，采用抽样调查的方式 D、若平均数相同的甲、乙两组数据 $s_{甲}^{2}$ =0.3， $s_{乙}^{2}$ =0.02，则甲组数据更稳定

查看解析
9、小明利用一次函数和二次函数知识，设计了一个计算程序，其程序框图如图甲所示，输入x的值为-2时，输出y的值为1；输入x的值为2时，输出y 的值为3；输入x的值为3时，输出y的值为6.

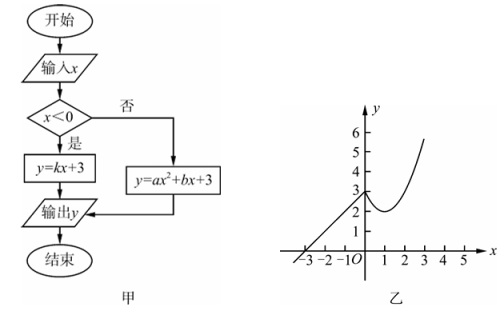(1)、请直接写出k，a，b的值.

(2)、小明在平面直角坐标系中画出了关于x的函数图象，如图乙.
①当y随x的增大而增大时，求x的取值范围.
②若关于x的方程ax²+bx+3-t=0（t为实数），当0<x<4时无解，求t的取值范围.
③若在函数图象上有点P，Q（P与Q不重合）.P的横坐标为m，Q的横坐标为-m+1.小明对P，Q 之间（含P，Q两点）的图像进行研究，当图像对应函数的最大值与最小值均不随m的变化而变化，请直接写出 m的取值范围.

查看解析
10、一条河上横跨着一座宏伟壮观的悬索桥.桥梁的缆索L₁与缆索L₂均呈抛物线型，桥塔AO与桥塔BC均垂直于桥面，如图所示，以O为原点，直线FF'为x轴，桥塔AO所在直线为y轴，建立平面直角坐标系.
已知：缆索L₁所在抛物线与缆索L₂所在抛物线关于y轴对称，桥塔AO与桥塔BC之间的距离OC=100m，AO=BC=17m，缆索L₁的最低点P到FF'的距离PD=2m（桥塔的粗细忽略不计）.

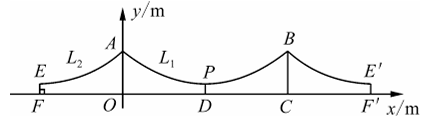(1)、求缆索L₁所在抛物线的函数表达式.

(2)、点E在缆索L₂上，EF⊥FF'，且EF=2.6m，FO<OD，求FO的长.

查看解析
11、已知二次函数y=-x²+bx+c.

(1)、当b=4，c=3时，
①求该函数图象的顶点坐标.
②当-1≤x≤3时，求y的取值范围.

(2)、当x≤0时，y的最大值为2；当x>0时，y的最大值为3，求二次函数的表达式.

查看解析
12、在如图所示的平面直角坐标系中，有一斜坡 OA，从点 O 处抛出一个小球，落到点 $A (3, \frac{3}{2})$ 处. 小球在空中所经过的路线是抛物线 $y = - x^{2} + b x$ 的一部分.

(1)、求抛物线的函数表达式.

(2)、求抛物线最高点的坐标.

(3)、斜坡上点B 处有一棵树，B是OA 的三等分点，小球恰好越过树的顶端 C，求这棵树的高度.

查看解析
13、如图，矩形ABCD的四个顶点都在格点（网格线的交点）上，对角线AC，BD 相交于点E，反比例函数y= $\frac{k}{x}$ （x>0）的图象经过点A.

(1)、求这个反比例函数的表达式.

(2)、将矩形ABCD向左平移，当点E落在这个反比例函数的图象上时，试求平移的距离.

查看解析
14、如图，在同一直角坐标系中，一次函数 $y = - x + b$ 和反比例函数 $y = \frac{9}{x}$ 的图象交于点 A（1，m），B（n，1）.

(1)、求点A，点B的坐标及一次函数的表达式.

(2)、根据图象，直接写出不等式 $- x + b > \frac{9}{x}$ 的解集.

查看解析
15、已知一次函数y=kx与反比例函数y= $\frac{3}{x}$ 的图象都经过点A（m，1）.

(1)、求一次函数的表达式.

(2)、求一次函数与反比例函数图象的另一个交点的坐标.

查看解析
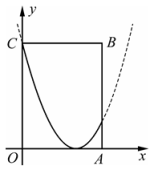
16、在平面直角坐标系xOy中，某个图形上的点都在一边平行于x轴的矩形内部（包括边界），这些矩形中面积最小的矩形称为该图形的关联矩形.例如：如图所示，函数y= （x-2）²（0≤x≤3）的图象（抛物线中的实线部分），它的关联矩形为矩形OABC.若二次函数y= $\frac{1}{4}$ x²+bx+c（0≤x≤3）图象的关联矩形恰好也是矩形OABC，则b=.

查看解析
17、已知 $y = \sqrt{3} x$ 与 $y = \frac{k}{x} (x > 0)$ 的图象交于点A（2，m），B为y轴上一点，将 $△ O A B$ 沿OA翻折，使点B恰好落在 $y = \frac{k}{x} (x > 0)$ 上点C处，则B点坐标为.

查看解析
18、某函数满足当自变量x=1时，函数值y=0；当自变量x=0时，函数值y=1.请写出一个满足条件的函数表达式： .

查看解析
19、在一定条件下，乐器中弦振动的频率f与弦长l成反比例关系，即f= $\frac{k}{l}$ （k为常数.k≠0），若某乐器的弦长l为0.9米，振动频率f为200赫兹，则k的值为.

查看解析
20、在平面直角坐标系中，若点P（a-1，a+1）在y轴上，则a的值是.

查看解析

上一页 964 965 966 967 968 下一页跳转

年龄范围（岁）	人数（人）
90~91	25
92~93
94~95
96~97	11
98~99	10
100~101	m