相关试卷

1、把多项式 $4 x^{2} y - 4 x y^{2} - x^{3}$ 分解因式的结果是( ).

A、4xy(x-y)-x³ B、-x(x-2y)² C、 $x (4 x y - 4 y^{2} - x^{2})$ D、 $- x (- 4 x y + 4 y^{2} + x^{2})$

查看解析
2、若 $x^{2} + 2 (m - 3) x + 16$ 是关于x的完全平方式，则m 的值为.

查看解析
3、分解因式：

(1)、 $x^{3} + 3 x^{2} - 4 x - 12 =$ .

(2)、 ${(x^{2} + 3 x)}^{2} - 2 (x^{2} + 3 x) - 8 =$ .

查看解析
4、分解因式：

(1)、 $a^{3} + a b^{2} - 2 a^{2} b =$ .

(2)、 ${(x - 1)}^{2} - 2 (x - 1) + 1 =$ .

(3)、 $a^{2} - 2 a b + b^{2} - 1 =$ .

(4)、 $x^{2} - y^{2} - 4 x + 4 =$ .

查看解析
5、把下列各式分解因式：

(1)、 $6 y^{2} - 11 y - 10 .$

(2)、 $8 x^{2} - 2 x y - 3 y^{2} .$

查看解析
6、分解因式： $x^{3} + 6 x^{2} + 11 x + 6 .$

查看解析
7、阅读理解.
观察下列因式分解的过程：
⑴ $x^{2} - x y + 4 x - 4 y .$
原式：=(x²-xy)+(4x-4y)=x(x-y)+4(x-y)=(x-y) ·(x+4).
⑵ $a^{2} - b^{2} - c^{2} + 2 b c .$
原式 $= a^{2} - (b^{2} + c^{2} - 2 b c) = a^{2} - {(b - c)}^{2} = (a + b - c) (a - b + c$ ).
第(1)题分组后能直接提公因式，第(2)题分组后能直接运用公式.仿照上述分解因式的方法，把下列各式分解因式：

(1)、 $a^{2} - a b + a c - b c .$

(2)、 $x^{2} - 4 y^{2} - z^{2} + 4 y z .$

查看解析
8、把下列各式分解因式：

(1)、 $(x^{2} + 5 x + 2) (x^{2} + 5 x + 3) - 12 .$

(2)、 $(x + 1) (x + 2) (x + 3) (x + 6) + x^{2}$ .

(3)、 $(x + y) (x + y + 2 x y) + (x y + 1) (x y - 1)$ .

查看解析
9、分解因式： ${(2 x - 3 y)}^{3} + {(3 x - 2 y)}^{3} - 125 {(x - y)}^{3} =$ .

查看解析
10、阅读以下材料：
对数的创始人是苏格兰数学家纳皮尔，纳皮尔发明对数是在指数书写方式出现之前，直到18世纪，瑞士数学家欧拉才发现指数和对数的联系.
对数的定义：一般地，若 $a^{x} = N (a⟩ 0 ， a \neq 1) ，$ 那么数x 叫作以a 为底 N 的对数，记作 $x = l o g_{a} N$ .比如指数式： $2^{4} = 16$ 可转化为对数式4=log₂16，对数式 $2 = {l o g}_{5} 25$ 可转化为指数式 $5^{2} = 25 .$
我们根据对数的定义可得到对数的一个性质：
$l o g_{a} (M \cdot N) = l o g_{a} M + l o g_{a} N (a > 0 ， a \neq 1 ， M > 0 ， N > 0)$ .理由如下：
设 $l o g_{a} M = m ， l o g_{a} N = n$ ，则 $M = a^{m} ， N = a^{n}$ ，
$∴ M \cdot N = a^{m} \cdot a^{n} = a^{m + n}$ ，
由对数的定义得 $m + n = {l o g}_{a} (M \cdot N)$ ，
又 $∵ m + n = {l o g}_{a} M + {l o g}_{a} N$ ，
∴ $l o g_{a} (M \cdot N) = l o g_{a} M + l o g_{a} N$ .
解决以下问题：

(1)、将指数式 $4^{3} = 64$ 转化为对数式.

(2)、证明 ${l o g}_{a} \frac{M}{N} = {l o g}_{a} M - {l o g}_{a} N (a⟩ 0 ， a \neq 1 ， M > 0 ， N > 0) .$

(3)、拓展运用：计算 ${l o g}_{3} 2 + {l o g}_{3} 6 - {l o g}_{3} 4 =$ .

查看解析
11、

(1)、有足够多的长方形和正方形卡片，如下图：
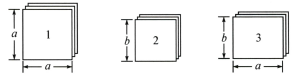
①如果选取的1号、2号、3号卡片分别为1张、2张、3张，可拼成一个长方形(不重叠无缝隙)，请画出这个长方形的草图，并运用拼图前后面积之间的关系说明这个长方形的代数意义.
这个长方形的代数意义是.
②小明想用类似方法解释多项式乘法 $(a + 3 b) (2 a + b) = 2 a^{2} + 7 a b + 3 b^{2} ，$ 那么需要用2号卡片张，3号卡片张.

(2)、利用图形面积可以解释代数恒等式的正确性，也可以解释不等式的正确性.
①根据下图所示图形写出一个代数恒等式.
②已知正数a，b，c和m，n，l，满足a+m=b+n=c+l=k.试构造边长为k的正方形，利用图形面积来说明 $a l + b m + c n < k^{2} .$

查看解析
12、有( )个整数n(不必是正的)可以使得 $4000 \cdot {(\frac{2}{5})}^{n}$ 的值是一个整数.

A、3 B、4 C、6 D、8 E、9

查看解析
13、在矩形ABCD内，将两张边长分别为a 和b(a>b)的正方形纸片按图①、图②两种方式放置(图①、图②中两张正方形纸片均有部分重叠)，矩形中未被这两张正方形纸片覆盖的部分用阴影表示，设图①中阴影部分的面积为S₁ ，图②中阴影部分的面积为S₂ ，当AD-AB=2时， $S_{2} - S_{1}$ 的值为( ).

A、2a B、2b C、2a-2b D、-2b

查看解析
14、已知 $2 5^{x} = 2000 ， 8 0^{y} = 2000$ ，则 $\frac{1}{x} + \frac{1}{y}$ 等于( ).

A、2 B、1 C、 $\frac{1}{2}$ D、 $\frac{3}{2}$

查看解析
15、

(1)、 $1 5^{16}$ 与 $3 3^{13}$ 的大小关系是： $1 5^{16}$ $3 3^{13}$ (填“>”“<”或“=”).

(2)、 $\frac{3^{2000} + 1}{3^{2001} + 1}$ 与 $\frac{3^{2001} + 1}{3^{2002} + 1}$ 的大小关系是： $\frac{3^{2000} + 1}{3^{2001} + 1}$ $\frac{3^{2001} + 1}{3^{2002} + 1}$ (填“<”“>”或“=”).

查看解析
16、如果 $\frac{4^{5} + 4^{5} + 4^{5} + 4^{5}}{3^{5} + 3^{5} + 3^{5}} \times \frac{6^{5} + 6^{5} + 6^{5} + 6^{5} + 6^{5} + 6^{5}}{2^{5} + 2^{5}} = 2^{n}$ ，那么n=.

查看解析
17、 19×19乘法表
印度人是用以下方法计算13×12，15×19的：
13×12=(13+2)×10+2×3=156，15×19=(15+9)×10+5×9=285.
一般来说，计算小于20的两个两位数的乘法，均可以采用类似的算法：把其中一个两位数加上另一个两位数的个位数，在所得和的后面添上一个0(即扩大10倍)，再加上原来两个两位数的个位数的乘积，其和即为所求.用这种算法很快可以制作19×19乘法表.

(1)、用以上算法计算：18×16==(写出计算过程).

(2)、若用(10+a)表示十位数为1、个位数为a的两位数，(10+b)表示十位数为1、个位数为b的两位数，请用整式的运算说明上述计算(10+a)(10+b)的方法的道理.

查看解析
18、已知 $1 0^{a} = 20 ， 10 0^{b} = 50 ，$ 则 $\frac{1}{2} a + b + \frac{3}{2}$ 的值为( ).

A、2 B、 $\frac{5}{2}$ C、3 D、 $\frac{9}{2}$

查看解析
19、已知 $2^{a} = 3 ， 2^{b} = 6 ， 2^{c} = 12$ ，则a，b，c 的关系是( ).

A、2b<a+c B、2b=a+c C、2b>a+c D、a+b>c

查看解析
20、如图，从边长为a 的大正方形中剪掉一个边长为b 的小正方形，将涂色部分沿虚线剪开，拼成右边的矩形.根据图形的变化过程写出的一个正确的等式是( ).

A、 ${(a - b)}^{2} = a^{2} - 2 a b + b^{2}$ B、 $a (a - b) = a^{2} - a b$ C、 ${(a - b)}^{2} = a^{2} - b^{2}$ D、 $a^{2} - b^{2} = (a + b) (a - b)$

查看解析

上一页 827 828 829 830 831 下一页跳转