-
1、如图是由四个全等的直角三角形和中间一个小正方形EFGH拼成的赵爽弦图，连结CE并延长，交BG于点M，交AB于点N.记△NAE的面积为S1 ， △CGM的面积为S2.
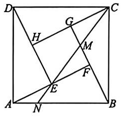
⑴若NA=NE，则的值为；
⑵若 且EF=9，则AE的长度为.
-
2、某校为了解学生在校午餐所需的时间，抽查了20名学生在校午餐所花的时间，获得如下数据(单位：分)：9，12，15，10，16，18，19，18，20，38，22，25，20，18，18，20，15，16，21，16.若将这些数据分为6组，制作频数表，则频数最大的组是第组(按从小到大排).
-
3、 在⊙O中，半径OA=2，弦则弦AB所对的圆周角的大小为.
-
4、 篮球比赛规则规定：赢一场得 2分，输一场得1分.某次比赛甲球队赢了x场，输了y场，积20分，则 y=(用含x的代数式表示).
-
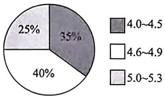
5、 国际上把5.0及以上作为正常视力，图是某校学生的视力情况统计图，已知该校视力正常的学生有500人，则未达到正常视力的学生人数为.
-
6、 已知三角形的两边长分别为3，4，则第三边的长可以是(写出一种即可).
-
7、 已知二次函数 当m≤x≤m+2时，函数y的最小值是-4，则m的取值范围是( )A、m≥1 B、m≤1 C、-1≤m≤1 D、0≤m≤2
-
8、某水文局测得一组关于降雨强度I和产汇流历时t的对应数据如下表(注：产汇流历时是指由降雨到产生径流所经历的时间)，根据表中数据，可得t关于I的函数表达式近似为( )
降雨强度I(mm/h)
4
6
8
10
12
14
产汇流历时t(h)
18.0
12.1
9.0
7.2
6.0
5.1
A、 B、 C、 D、 -
9、如图，某款扫地机器人的俯视图是一个等宽曲边三角形ABC(分别以正△ABC的三个顶点 A，B，C为圆心，AB长为半径画弧得到的图形).若AB=6，则曲边AB的长为( )
A、π B、2π C、6π D、12π -
10、不等式组 的解是( )A、x>3 B、x≤2 C、2<x≤5 D、3<x≤5
-
11、今有三人共车，二车空，二人共车，九人步.问人与车各几何.(选自《孙子算经》)现假设有x辆车，则可列方程( )A、3(x-2)=2x+9 B、3x-2=2x+9 C、3x-2=2(x+9) D、3(x-2)=2(x+9)
-
12、 如图，l∥AB，∠A=2∠B.若∠1=108°，则∠2的度数为( )
A、36° B、46° C、72° D、82° -
13、下列四幅图形中，表示两棵小树在同一时刻同一地点阳光下的影子的是( )A、
B、
C、
D、
-
14、家用冰箱冷冻室的温度需控制在-24℃与-4℃之间，则可将冷冻室的温度设为( )A、0℃ B、-3℃ C、-18℃ D、-25℃
-
15、定义一个运算： 如2*1=22-2×1=2，(-1)*2=-(-1)2+2×2=3.用表示大于m的最小整数，如<1>=2，<3.2>=4，<-3>=-2.按照上述规定，若整数x满足<(-2)*3>=-6，则x的值是.
-
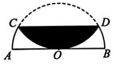
16、 如图，AB=6，以 AB 为直径作半圆，弦CD∥AB，将CD上方的图形沿CD向下折叠，使与直径AB恰好相切于点O，则图中阴影部分的面积为.
-
17、 已知二次函数y=(x-1)(x+3)，当-2≤x≤1时，y的取值范围是.
-
18、某校共有 1200 名学生.为了解学生的立定跳远成绩分布情况，随机抽取 100名学生的立定跳远成绩，画出如图所示的条形统计图，估计该校立定跳远成绩优秀的学生人数是.
-
19、 如图，在直角坐标系中，点A(0，4)，B(3，0)，线段AB绕点B按顺时针方向旋转45°得到线段BC，则点C的纵坐标为( )
A、5 B、 C、 D、 -
20、 如图，在等边三角形ABC中，点D，E分别在边BC，AC上，AD，BE交于点F.若AB=6，则EF的长为( )
A、2 B、 C、 D、