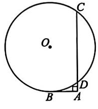
-
1、 如图，AB是⊙O的切线，B为切点，作AC⊥AB交AB于点A，AC交⊙O于C，D两点.若AB=3，AC=9，则⊙O的半径是
-
2、不等式 的解是.
-
3、在平面直角坐标系中，将点 P(-3，-2)水平向右平移a个单位后落在第四象限内，则a 的值可以是 .(写出一个即可)
-
4、为了了解“双减”背景下全国中小学生完成课后作业的时间情况，比较适合的调查方式是 (填“全面调查”或“抽样调查”).
-
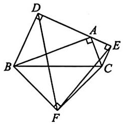
5、 如图，在△ABC中，∠BAC=90°，AB>AC.分别以△ABC的三边为斜边向外作等腰直角三角形ABD，BCF，CAE，连结 DF，EF.若△DEF与△ABC的面积比为5：2，则 tan∠ABC的值是( )
A、 B、 C、 D、 -
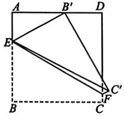
6、 如图，在正方形ABCD中，AB=3，点E，F分别在边AB，CD 上，∠EFD=60°.将四边形EBCF沿EF折叠得到四边形 EB'C'F，且点B'恰好在AD边上，连结 EC'，则EC'的长是( )
A、4 B、 C、2 D、 -
7、学习了“三角形中位线定理”后，在“△ABC中，D，E分别是边AB，AC上的点”这个前提条件下，某同学得到以下3个结论：
①若D是AB的中点，DE∥BC，则E是AC的中点；
②若D是AB的中点， 则E是AC的中点；
③若DE∥BC，DE=BC，则 D，E 分别是AB，AC的中点.
其中正确的是( )
A、①② B、①③ C、②③ D、①②③ -
8、古代算书《四元玉鉴》中有“两果问价”问题：“九百九十九文钱，甜果苦果买一千，甜果九个十一文钱，苦果七个四文钱.试问甜苦果几个.”该问题的译文是：九百九十九文钱买了甜果和苦果共一千个，已知十一文钱可买九个甜果，四文钱可买七个苦果，那么甜果、苦果各买了多少个?设甜果买了x个，苦果买了y个，根据题意，可列方程组是 ( )A、 B、 C、 D、
-
9、 □ABCD的对角线AC，BD交于点O，则AO不可能是△ABD的( )A、中线 B、高线 C、中位线 D、角平分线
-
10、下列运算正确的是( )A、 B、 C、 D、
-
11、 在-4，-1，0，1这四个数中，比-2小的数是( )A、-4 B、-1 C、0 D、1
-
12、 已知二次函数
⑴若点(b-2，c)在该函数图象上，则b的值为；
⑵若点(b-2，y1)，(2b，y2)，(2b+6，y3)都在该函数图象上，且则b的取值范围为.
-
13、 如图，在菱形ABCD中，点E在BC上，将△ABE沿AE翻折得到△AGE，点G在BC的延长线上，AG与CD相交于点F.若 则tanB的值为.
-
14、如图，过⊙O外一点P作圆的切线PA，PB，A，B为切点，AC为⊙O的直径，设∠P=m°，∠C=n°，则m，n之间的数量关系为.
-
15、 甲、乙、丙、丁四人进行射击测试，四人射击成绩的平均数均是9.2环，方差分别为 0.56 环2 ， 环2 环2 ， 0.45环2 ， 则成绩最稳定的是.
-
16、如图，四个全等的直角三角形拼成“赵爽弦图”，其中四边形ABCD与四边形EFGH都是正方形.连结DG并延长，交BC于点P，P为BC的中点.若EF=2，则AE的长为( )
A、4 B、 C、 D、 -
17、如图是一个直三棱柱及其左视图，则左视图中m的值为( )
A、2.4 B、3 C、4 D、5 -
18、 如图，已知正方形ABCD的面积为9，AB∥x轴.它的两个顶点B，D是反比例函数 的图象上两点.若点 D 的坐标是(m，n)，则m-n的值为( )
A、3 B、-3 C、 D、 -
19、如图，平行于主光轴MN的光线AB和CD经过凸透镜的折射后，折射光线BE，DF交于主光轴MN上一点P.若∠ABE=150°，∠CDF=170°，则∠EPF的度数是( )
A、20° B、30° C、40° D、50° -
20、我国已建成全球规模最大的光纤和移动宽带网络.截至2024年3月底，光缆线路总长度约为65580000千米，其中 65580000用科学记数法可表示为( )A、65.58×106 B、6.558×107 C、6.558×106 D、