-
1、某小组5名学生的某次考试成绩如下(单位:分):80、85、90、88、92,则这组数据的中位数是( )A、85 B、87 C、88 D、90
-
2、方程的解是 , 则的值( )A、 B、 C、 D、无解
-
3、下列运算正确的是( )A、 B、 C、 D、
-
4、垃圾分类功在当代利在千秋,下列垃圾分类指引标志图形中,是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、
-
5、计算( )A、 B、 C、 D、
-
6、我们定义:过三角形的一个顶点的线段将三角形分成两个三角形,其中一个三角形与原三角形相似,且相似比为 , 则原三角形叫做“友好三角形”;
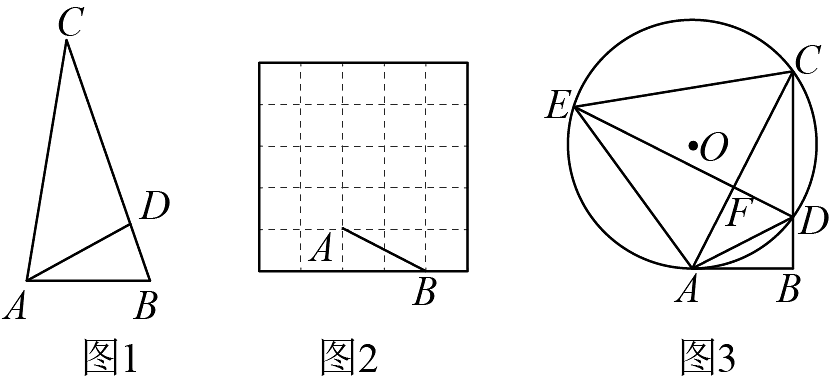 (1)、如图1,已知在中, , , 求证:是“友好三角形”;(2)、如图2,在的网格图中,点A、B在格点上,请在图中画出一个符合条件的“友好三角形” , 要求点在格点上;(3)、如图3,在(1)的条件中,作的外接圆 , 点是上的一点, , 连接DE;
(1)、如图1,已知在中, , , 求证:是“友好三角形”;(2)、如图2,在的网格图中,点A、B在格点上,请在图中画出一个符合条件的“友好三角形” , 要求点在格点上;(3)、如图3,在(1)的条件中,作的外接圆 , 点是上的一点, , 连接DE;①设 , , 求关于的函数关系式;
②当时,求的半径.
-
7、如图,是的角平分线,过点D作交于点E.交于点F.
 (1)、求证:四边形为菱形;(2)、如果 , , , 求菱形的边长.
(1)、求证:四边形为菱形;(2)、如果 , , , 求菱形的边长. -
8、为了进一步提升学生的科学素养,某学校计划在七年级开设“人工智能”、“无人机”、“创客”、“航模”四门校本课程,要求每人必须参加,并且只能选择其中一门课程,为了解学生对这四门课程的选择情况,学校从七年级全体学生中随机抽取部分学生进行问卷调查,并根据调查结果绘制成如图1和2所示的条形统计图和扇形统计图(部分信息未给出).

请你根据以上信息解决下列问题:
(1)、参加问卷调查的学生人数为__________,补全条形统计图(画图并标注相应数据);(2)、在扇形统计图中,选择“航模”课程的学生占%,所对应的圆心角度数是;(3)、若该校七年级一共有1200名学生,试估计选择“创客”和“人工智能”课程的学生有多少人? -
9、先化简: , 然后从中选一个合适的整数作为x的值代入求值.
-
10、如图,在等腰直角三角形中, , 点A、B在抛物线上,点C在y轴上,A、B两点的横坐标分别为1和 , b的值为 .

-
11、如图,在中, , , , 的垂直平分线分别交 , 于点D,E,则的长为 .

-
12、分式方程的解是 .
-
13、一组数据:2、0、2、4,若添加一个数据2,则发生变化的统计量是( )A、平均数 B、中位数 C、众数 D、方差
-
14、如图从三个不同的方向看,不可能的形状图是( )
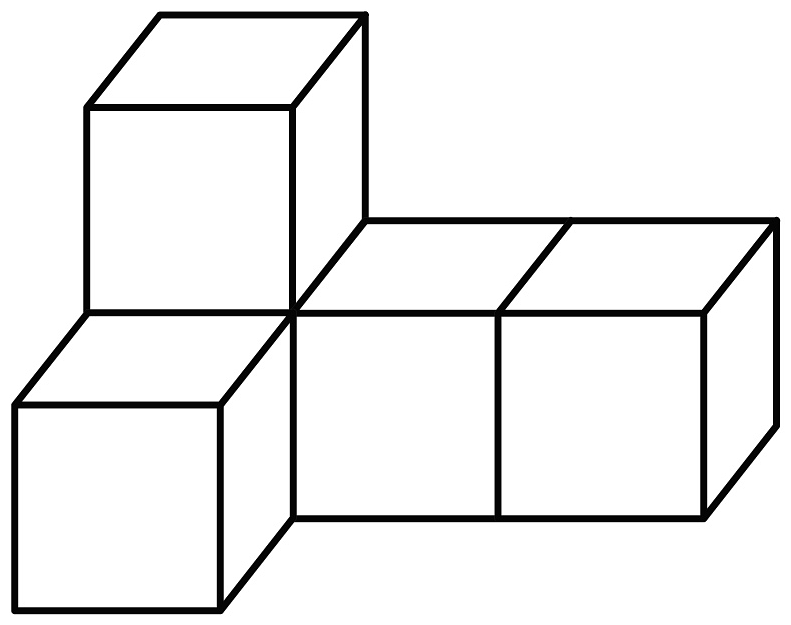 A、
A、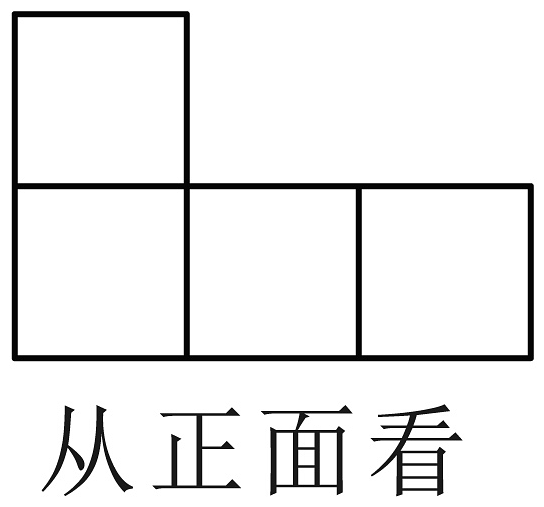 B、
B、 C、
C、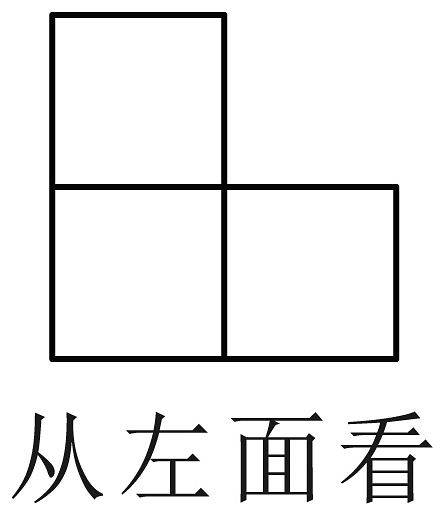 D、
D、
-
15、近年来,我国快递行业发展质效不断提升,据国家邮政局统计,截至年月日,我国快递业务量首次突破亿件,刷新历史记录,亿快件背后,是更加繁荣活跃的快递市场,数据亿用科学记数法表示为( )A、 B、 C、 D、
-
16、如果规定汽车向东行驶3千米记作千米,那么向西行驶5千米记作( )千米A、 B、 C、 D、3
-
17、已知,抛物线(),与x轴交于A,B,(点A在点B的左侧)与y轴交于点C,顶点为点D.
 (1)、抛物线的对称轴为 (用含有a的式子表示);(2)、若当时,函数值y随着x的增大而减小,求a的取值范围;(3)、如图1,当时,点为第四象限的抛物线上一点,过点E作轴与抛物线另外一个交点为点F.
(1)、抛物线的对称轴为 (用含有a的式子表示);(2)、若当时,函数值y随着x的增大而减小,求a的取值范围;(3)、如图1,当时,点为第四象限的抛物线上一点,过点E作轴与抛物线另外一个交点为点F.①连接 , 过点E作轴,交于点H,以为邻边构造矩形 , 当矩形的周长为时,求m的值;
②以所在直线为对称轴将抛物线位于下方的部分翻折,若翻折后所得部分与x轴有交点,且交点都位于x轴正半轴,请直接写出n的取值范围.
-
18、【问题初探】
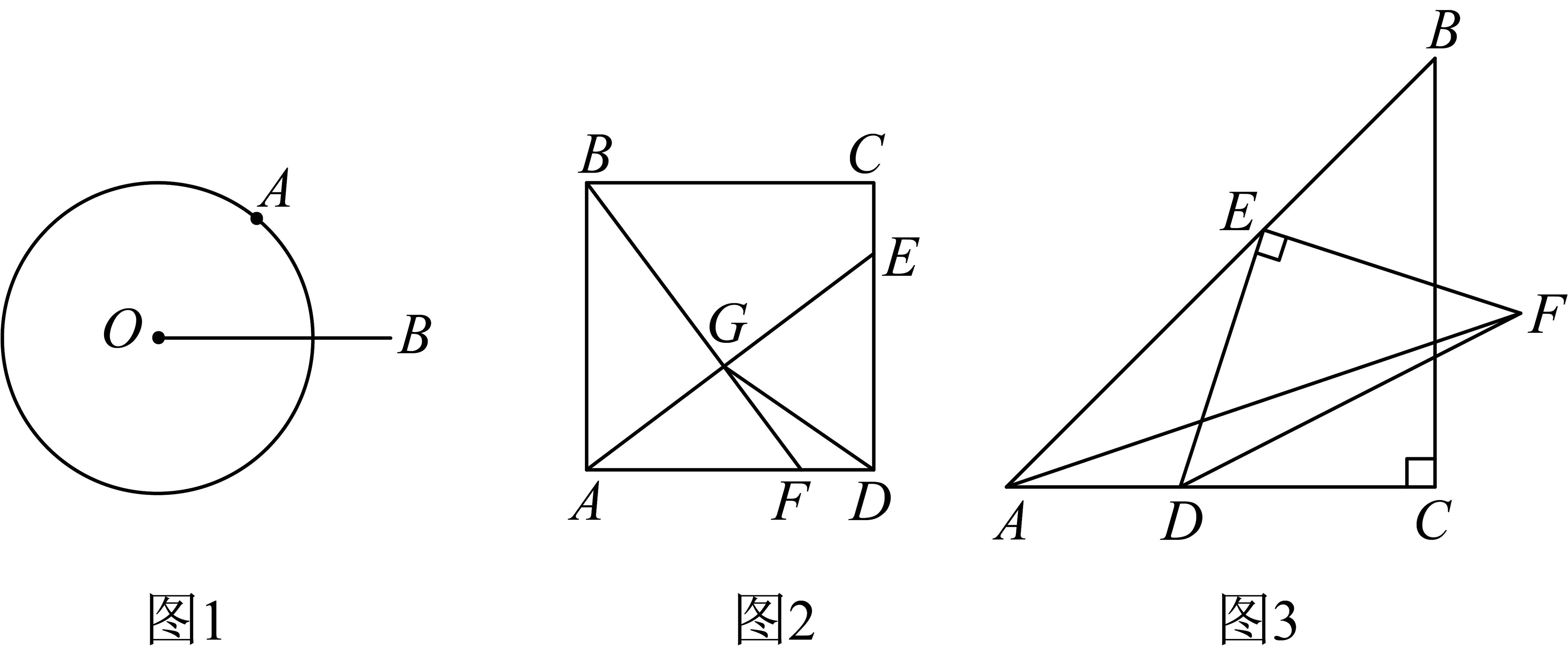
(1)如图1,动点A在半径为2的上,若 , 直接写出的最小值.
由于和都是定长,当点A,B,O形成三角形时,霖霖想到了“三角形两边之差小于第三边”,由此可知当点A在上时对应的就是最小的情形.按照霖霖的思路,请直接写出最小值.
【类比分析】
(2)如图2,点E和F分别是边长为4的正方形边和上的两个动点,且 , 连接和交于点G,连接 , 求的最小值.
霖霖尝试着绘制了点E在不同位置的几张图,目测始终都是直角,于是联想到了“圆周角所对的弦是直径”,也就是说“点G是正方形内以为直径的圆弧上的点”,进而本题可以类比图1获解,清按照霖霖的思路完成求最小值的解题过程.以下是证明的部分过程
证明:

∴可判断点G的轨迹,即的最小值为_________.
请补全缺失的证明过程.
【学以致用】
(3)如图3,是两块等腰直角三角板, , , . 当点D和E同时在边和上滑动时,点F也随之移动,若连接 , 则的最大值是_________.
-
19、图1是煤油温度计,该温度计的左侧是华氏温度(),右侧是摄氏温度().华氏温度与摄氏温度之间存在着某种函数关系,小明通过查阅资料和观察温度计,得到了如表所示的数据.
摄氏温度值
0
10
20
30
40
华氏温度值
32
50
68
86
104
 (1)、在如图2所示的平面直角坐标系中描出上表相应的点,并用平滑的线进行连接;(2)、求y与x之间的函数解析式;(3)、某种疫苗需低温保存,其活性只能在某温度区间(摄氏温度)内维持,在该温度区间内,任意摄氏温度与其对应的华氏温度的数值相差的最大值为16.求该温度区间的最大温差是多少摄氏度.
(1)、在如图2所示的平面直角坐标系中描出上表相应的点,并用平滑的线进行连接;(2)、求y与x之间的函数解析式;(3)、某种疫苗需低温保存,其活性只能在某温度区间(摄氏温度)内维持,在该温度区间内,任意摄氏温度与其对应的华氏温度的数值相差的最大值为16.求该温度区间的最大温差是多少摄氏度. -
20、一项知识问答竞赛要求以团队方式参赛,每个团队20名选手.某校准备参加此项竞赛,前期组建了两个团队,经过一段时间的培训后,对两个团队进行了一次预赛,对成绩(百分制)进行了整理、描述和分析.下面给出了部分信息.
a.一队成绩的频数分布直方图如下(数据分成4组:):

b.二队成绩如下:
68 69 70 70 71 73 77 78 80 81
82 82 82 82 83 83 83 86 91 94
c.一、二两队成绩的平均数、众数、中位数如下:
平均数
众数
中位数
一队
79.6
77
P
二队
79.25
m
q
根据以上信息,回答下列问题:
(1)、m的值为___________,p___________q(填“”“”或“”);(2)、若两队都各去掉一个最高分和一个最低分,则下列判断正确的是___________;A.一队成绩的方差增大,二队成绩的方差减小 B.两队成绩的方差都增大
C.一队成绩的方差减小,二队成绩的方差增大 D.两队成绩的方差都减小
(3)、为了选出冲击个人冠军的种子选手,学校对这次成绩90分以上的甲、乙、丙三位同学又单独进行了5次测试,平均数较大的选手排序靠前,若平均数相同,则方差较小的选手排序靠前.这5次测试的成绩如下:测试1
测试2
测试3
测试4
测试5
甲
90
94
90
94
91
乙
91
92
92
92
93
丙
93
90
92
93
k
若丙的排序居中,则表中k(k为整数)的值为___________.