-
1、为做好青少年禁毒教育宣传工作,某校开展了主题为“珍爱生命,拒绝毒品”的知识竞赛(共20题,每题5分,满分100分).该校从学生成绩都不低于80分的九年级(1)和(3)班中,各随机抽取了20名学生成绩进行整理,绘制了不完整的统计表、条形统计图及分析表.
【收集数据】
九年级(1)班20名学生成绩:85,95,100,90,90,80,85,90,80,100,80,85,95,90,95,95,95,95,100,95.
九年级(3)班20名学生成绩:90,80,100,95,90,85,85,100,85,95,85,90,90,95,90,90,95,90,95,95.
【描述数据】九年级(1)班20名学生成绩统计表
分数
80
85
90
95
100
人数
3
3
a
7
3
九年级(3)班20名学生成绩条形统计图

【分析数据】九年级(1)班和(3)班20名学生成绩统计表
统计量/班级
平均数
中位数
众数
方差
九年级(1)班
m
n
95
41.5
九年级(3)班
91
90
p
26.5
【应用数据】根据以上信息,回答下列问题:
(1)、请补全条形统计图;(2)、填空:________,________,________;(3)、你认为哪个班级的成绩更好一些?请说明理由;(4)、从上面5名的100分的学生中,随机抽取2名学生参加市级知识竞赛,请用列表法或画树状图法求所抽取的2名学生恰好在同一个班级的概率. -
2、如图,在中,延长到E点,使 , 连结 , 与交于点O,连结、 .
 (1)、求证:;(2)、求证: .
(1)、求证:;(2)、求证: . -
3、解不等式组: , 并在数轴上表示其解集.

-
4、计算: .
-
5、如图,等边的顶点A在双曲线且底边在x轴上,F为中点,O为的中点,连接交于E,四边形的面积为4,则 .
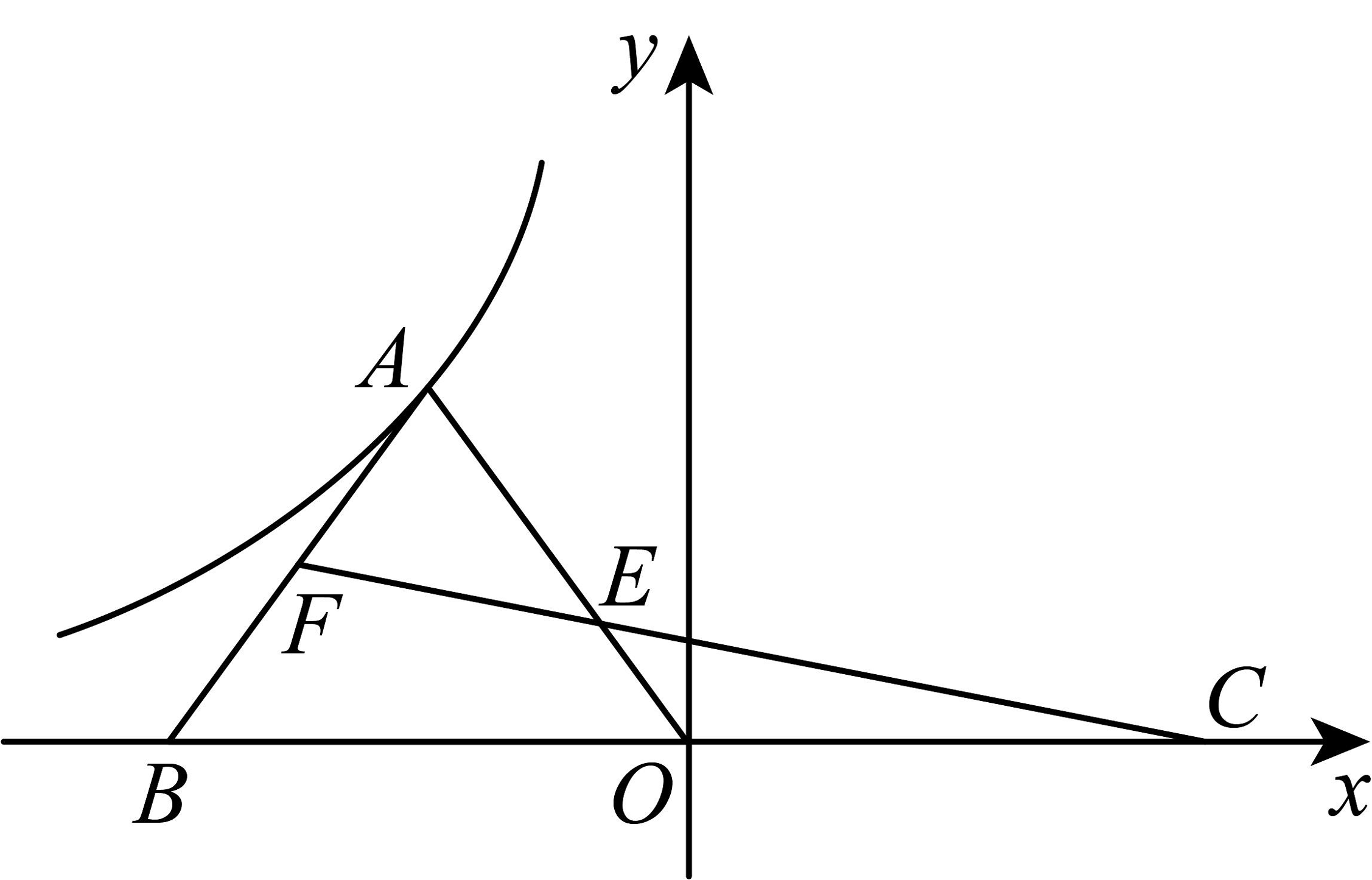
-
6、如图,点是矩形中边上的一点,沿折叠为 , 点落在上.若的大小为 , 且满足 , 则的值为 .

-
7、如图,过圆外一点向圆O做两条切线分别是和 , 已知圆的半径为3, , 求弦 .

-
8、如图,小明同学按如下步骤作四边形:①画2个单位长度的线段;②以点A、C为圆心,2个单位长为半径画弧,分别于点B,D;③连接 , 则的大小是 .

-
9、分式有意义,则的取值范围是 .
-
10、新定义:一动点到定直线的最小距离我们称为“亲密距离”.如图,在平面直角坐标系中,直线的表达式为 , 直线的表达式为 , 平分 , 点B为中点,延长使 , 动点P在平面内运动,恒有 , 点P到直线OD的“亲密距离”为d,求d的值是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
11、已知是关于x的方程的一个实数根,则锐角的度数为( )A、 B、 C、 D、
-
12、已知一次函数与反比例函数的图像交于、两点,则不等式的解集为( )A、 B、或 C、或 D、或
-
13、已知点在x轴上,则( )A、0 B、 C、1 D、
-
14、已知关于x的方程的解是 , 则不等式的解集为( )A、 B、 C、 D、
-
15、某小组5名学生的某次考试成绩如下(单位:分):80、85、90、88、92,则这组数据的中位数是( )A、85 B、87 C、88 D、90
-
16、方程的解是 , 则的值( )A、 B、 C、 D、无解
-
17、下列运算正确的是( )A、 B、 C、 D、
-
18、垃圾分类功在当代利在千秋,下列垃圾分类指引标志图形中,是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、
-
19、计算( )A、 B、 C、 D、
-
20、我们定义:过三角形的一个顶点的线段将三角形分成两个三角形,其中一个三角形与原三角形相似,且相似比为 , 则原三角形叫做“友好三角形”;
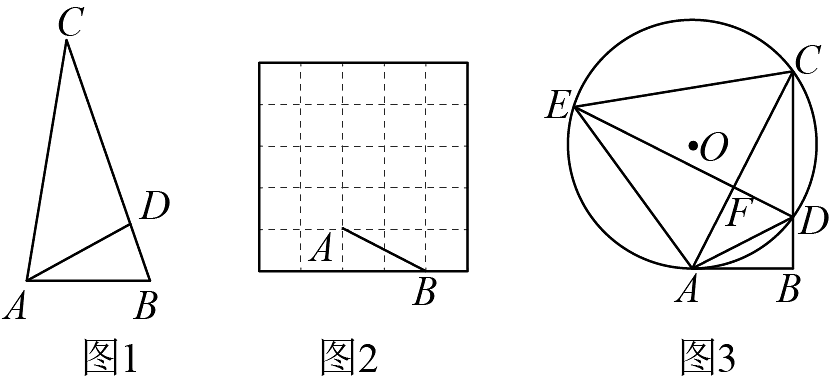 (1)、如图1,已知在中, , , 求证:是“友好三角形”;(2)、如图2,在的网格图中,点A、B在格点上,请在图中画出一个符合条件的“友好三角形” , 要求点在格点上;(3)、如图3,在(1)的条件中,作的外接圆 , 点是上的一点, , 连接DE;
(1)、如图1,已知在中, , , 求证:是“友好三角形”;(2)、如图2,在的网格图中,点A、B在格点上,请在图中画出一个符合条件的“友好三角形” , 要求点在格点上;(3)、如图3,在(1)的条件中,作的外接圆 , 点是上的一点, , 连接DE;①设 , , 求关于的函数关系式;
②当时,求的半径.