相关试卷
-
1、计算: .
-
2、如图,正方形纸片中,E是上一点,将纸片沿过点E的直线折叠,使点A落在上的点G处,点B落在点H处,折痕交于点F . 若 , , 则 .
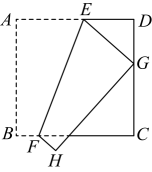
-
3、A , B两地相距 , 甲、乙两人骑车同时分别从A , B两地相向而行.假设他们都保持匀速行驶,甲、乙两人各自到A地的距离与骑车时间的关系如图所示,则他们相遇时距离A地 .
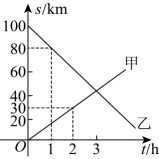
-
4、如图,两条直线 , 分别经过正六边形的顶点B , C , 且 . 当时, .
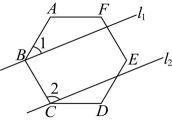
-
5、在一个不透明的袋中有2个红球、3个黄球和4个白球,这些球除颜色外都相同.从中随机摸出一个球,这个球是红球的概率为 .
-
6、已知一个正方形的面积为2,则其边长为 .
-
7、已知二次函数(a , b , c为常数,)图像的顶点坐标是 , 且经过 , 两点, . 有下列结论:
①关于x的一元二次方程有两个不相等的实数根;
②当时,y的值随x值的增大而减小;③;
④;⑤对于任意实数t , 总有 .
以上结论正确的有( )
A、5个 B、4个 C、3个 D、2个 -
8、如图,在中,按如下步骤作图:
①在和上分别截取 , , 使 , 分别以点M和N为圆心,以大于的长为半径作弧,两弧在内交于点O , 作射线交于点D ,
②分别以点C和D为圆心,以大于的长为半径作弧,两弧相交于点P和Q , 作直线交于点E , 交于点F .
根据以上作图,若 , , , 则线段的长为( )
 A、 B、 C、5 D、
A、 B、 C、5 D、 -
9、某学校食堂准备了A , B , C , D四种营养套餐,如果小明和小亮每人随机选择其中一种营养套餐,则他们恰好选到同一种营养套餐的概率是( )A、 B、 C、 D、
-
10、如图,在由边长为1个单位长度的小正方形组成的网格中,点A , B , C , D , E都在网格的格点上,则下列结论正确的是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
11、已知 , 则下列不等式一定成立的是( )A、 B、 C、 D、
-
12、下列运算正确的是( )A、 B、 C、 D、
-
13、下列图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、
-
14、2025年“五一”假期,济南市图书馆推出全民阅读文化市集、集邮展销等活动,累计接待读者96110人次,数据96110用科学记数法表示为( )A、 B、 C、 D、
-
15、如图是由几个大小相同的小立方块搭成的几何体,其主视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、
-
16、下列各数中为负数的是( )A、 B、0 C、2 D、
-
17、如图,在正方形中,E,F分别是 , 上的点, , 相交于点P,且 .
 (1)、如图1,求证:;(2)、若 , , 求的长度;(3)、如图2, , , 点F在线段上运动时(点F不与C、D重合),四边形是否能否成为菱形?请说明理由.
(1)、如图1,求证:;(2)、若 , , 求的长度;(3)、如图2, , , 点F在线段上运动时(点F不与C、D重合),四边形是否能否成为菱形?请说明理由. -
18、在平面直角坐标系中,的坐标为 , , , 并求:
 (1)、画出 , 其中 , , ;(2)、将向左平移3个单位后,变为 , 写出的坐标;(3)、求的面积.
(1)、画出 , 其中 , , ;(2)、将向左平移3个单位后,变为 , 写出的坐标;(3)、求的面积. -
19、如图, , , E,F是垂足, . 求证: .

-
20、如图,在平行四边形的边上分别取一个点E,F,使得 , 连接 . 求证:四边形是平行四边形.
