相关试卷
-
1、已知 , , 则( )A、14.36 B、143.6 C、45.4 D、454
-
2、如图,在三角形中, , , , 垂足为点D , 则的长可能是( )
 A、4 B、6 C、8 D、10
A、4 B、6 C、8 D、10 -
3、在实数 , 0, , , , , (相邻两个6之间1的个数逐次加1)中,无理数有( )A、2个 B、3个 C、4个 D、5个
-
4、下列计算中,结果正确的是( )A、 B、 C、 D、
-
5、我国古代数学的发展历史源远流长,在历代数学家的不懈探索中,诞生了很多重大的数学发现.下列有关我国古代数学发现的图示中,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、
-
6、 如图,平面直角坐标系中有三点 , , , 其中满足 . 平移线段得到线段 , 点的对应点为点 , 连接 .
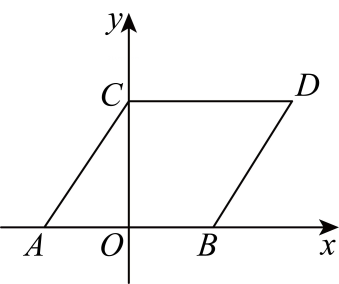 (1)、填空: , ;(2)、轴上是否存在点 , 使得三角形的面积是平行四边形的面积的2倍,若存在这样的点,求出点的坐标;若不存在,请说明理由.
(1)、填空: , ;(2)、轴上是否存在点 , 使得三角形的面积是平行四边形的面积的2倍,若存在这样的点,求出点的坐标;若不存在,请说明理由. -
7、 某中学响应“阳光体育”活动的号召,准备从体育用品商店购买一些排球、足球和篮球,排球和足球的单价相同,同一种球的单价相同,若购买2个足球和3个篮球共需340元,购买4个排球和5个篮球共需600元.(1)、求购买一个足球,一个篮球分别需要多少元?(2)、该中学根据实际情况,需从体育用品商店一次性购买三种球共100个,且购买三种球的总费用不超过6000元,求这所中学最多可以购买多少个篮球?
-
8、 某区准备组织部分学校的中小学生到A , B , C , D , E五个景区“一日游”,每名学生只能在五个景区中任选一个.为估计到各景区旅游的人数,随机抽取这些学校的部分学生,进行了“五个景区,你最想去哪里”的问卷调查,在统计了所有的调查问卷后将结果绘制成如图所示的统计图.
 (1)、求参加问卷调查的学生数,并将条形统计图补充完整;(2)、若参加“一日游”的学生为人,请估计到A景区旅游的人数.
(1)、求参加问卷调查的学生数,并将条形统计图补充完整;(2)、若参加“一日游”的学生为人,请估计到A景区旅游的人数. -
9、 如图,已知: , , 那么直线与的位置关系如何?并说明理由.
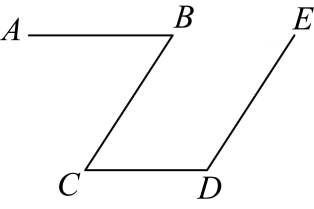
答: ▲ .
理由:(已知)
▲ ( )
(已知)
▲ ( )
▲ ( )
-
10、(1)、计算:;(2)、解方程组: .
-
11、 若不等式组无解,则m的取值范围是 .
-
12、 不等式解集是 .
-
13、 如图,在平面直角坐标系中,从点 , , 依此扩展下去,则的坐标为( )
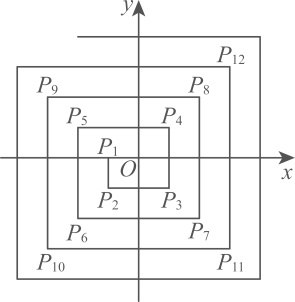 A、 B、 C、 D、
A、 B、 C、 D、 -
14、 如图,点在的延长线上,下列条件能判断的是( )
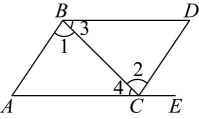 A、 B、 C、 D、
A、 B、 C、 D、 -
15、 下列调查中,适宜采用全面调查方式的是( )A、旅客上飞机前的安全检查 B、对广州市七年级学生身高现状的调查 C、对某品牌食品安全的调查 D、对一批灯管使用寿命的检查
-
16、 一个正方形的面积是11,估计它的边长大小在( )A、在1和2之间 B、在2和3之间 C、在3和4之间 D、在4和5之间
-
17、 在实数(每两个1之间0的个数依次增加1)中,无理数有( )A、1个 B、2个 C、3个 D、4个
-
18、 下列方程组中,解为的是( )A、 B、 C、 D、
-
19、 已知 , 下列不等式变形中正确的是( )A、 B、 C、 D、
-
20、 下列各图中,与是对顶角的是( )A、
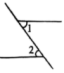 B、
B、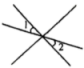 C、
C、 D、
D、