-
1、如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“”方向排列,如 , , , , , , ……,根据这个规律探索可得,第2025个点的坐标为 .

-
2、如图,在平面直角坐标系中,已知的顶点坐标分别为 , , . 若在第二象限内有一点 , 且四边形的面积是的面积的 , 则点P的坐标为 .

-
3、已知线段 , 轴,若点M坐标为 , 点N在第二象限,则N点的坐标为 .
-
4、在平面直角坐标系中,已知点 , 长度为3的线段与x轴平行,则点Q的坐标是 .
-
5、将点向右平移1个单位长度,再向下平移3个单位长度后,得到点 , 则点的坐标为 .
-
6、在平面直角坐标系中,已知点在轴上,则的值是 .
-
7、点到y轴的距离为 .
-
8、如图,一个粒子在第一象限和x轴,y轴的正半轴上运动,在第1秒内,它从原点运动到 , 接着它按图所示在x轴,y轴的平行方向来回运动,即…,且每秒运动一个单位长度,那么2023秒时,这个粒子所处位置为( )
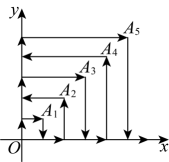 A、 B、 C、 D、
A、 B、 C、 D、 -
9、如图,将一个含角的直角三角板的斜边放在x轴上,O为坐标原点,观察尺规作图的痕迹,若点A的坐标为 , 则点C的横坐标为( )
 A、 B、 C、1 D、
A、 B、 C、1 D、 -
10、已知在第二象限内的点的坐标为 , 且点到两坐标轴的距离相等,则点的坐标是( )A、 B、 C、或 D、或
-
11、在平面直角坐标系中,点的坐标是 , 作点关于轴的对称点,得到点 , 再将点向下平移4个单位,得到点 , 则点的坐标是( )A、 B、 C、 D、
-
12、如图,这是某动物园大门口展示的动物园平面示意图,若以大门所在的位置为原点建立平面直角坐标系 , 则其他4个景点大致用坐标表示错误的是( )
 A、熊猫馆 B、驼峰 C、猴山 D、百鸟园
A、熊猫馆 B、驼峰 C、猴山 D、百鸟园 -
13、在平面直角坐标系中,点在轴上,则的值为( )A、1 B、 C、2 D、
-
14、在平面直角坐标系中,点在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限
-
15、如图,已知是等边三角形, , 点P从点A出发,沿射线以的速度运动,过点P作交射线于点E,同时点Q从点C出发沿的延长线以的速度运动,连接、 , 设点P的运动时间为 .
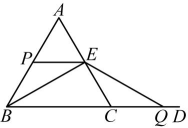 (1)、当点P在边上,且不与点、重合时,求证:;(2)、直接写出的长(用含t的代数式表示);(3)、在不添加字母和连接其它线段的条件下,当图中等腰三角形的个数大于3时,直接写出t的值和对应的等腰三角形的个数.(请写出所有的可能性)
(1)、当点P在边上,且不与点、重合时,求证:;(2)、直接写出的长(用含t的代数式表示);(3)、在不添加字母和连接其它线段的条件下,当图中等腰三角形的个数大于3时,直接写出t的值和对应的等腰三角形的个数.(请写出所有的可能性) -
16、如图在 , 中, , , , 点C,D,E三点在同一条直线上,连接 , 求证:
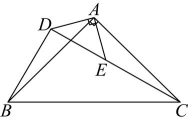 (1)、;(2)、试猜想 , 有何特殊的位置关系,并说明理由.
(1)、;(2)、试猜想 , 有何特殊的位置关系,并说明理由. -
17、如图,为斜边上的高,的平分线分别交 , 于点E、F, , 垂足为点G.
 (1)、求证:;(2)、若 , , , 求的面积.
(1)、求证:;(2)、若 , , , 求的面积. -
18、如图1,为等边内一点,将线段绕点逆时针旋转得到 , 连接 , 的延长线与交于点 , 与交于点 .
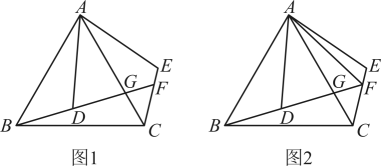 (1)、求证:;(2)、度;(3)、如图2,连接 , 平分吗?请说明理由.
(1)、求证:;(2)、度;(3)、如图2,连接 , 平分吗?请说明理由. -
19、如图,已知 , , .
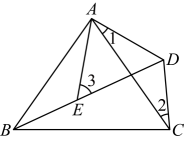 (1)、求证:;(2)、求的度数.
(1)、求证:;(2)、求的度数. -
20、如图:网格中每个小正方形的边长均为1,等腰的三个顶点在小正方形的顶点上,按要求完成以下问题:

在图中,用一条线段将分成2个全等的直角三角形.